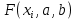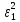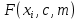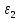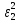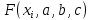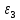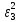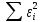Лабораторная работа 5 Метод наименьших квадратов студент гр. Ибс21 Проверил доцент кафедры пмиСА
 Скачать 77.98 Kb. Скачать 77.98 Kb.
|
|
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Саратовский государственный технический университет имени Гагарина Ю.А.» Кафедра «Прикладная математика и системный анализ» Лабораторная работа №5 «Метод наименьших квадратов» Выполнил: студент гр. ИБС-21 Проверил: доцент кафедры ПМиСА Коломоец А.А. Саратов, 2022 Лабораторная работа №5. Задание Построить приближающую функцию методом наименьших квадратов для зависимости, заданной следующей таблицей.
Для сравнения качества приближения рассмотреть три способа приближения заданной функции: а) в виде прямой  ; ;б) в виде степенной функции 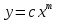 ; ;в) в виде квадратного трёхчлена 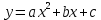 . .Основные теоретические положения Метод наименьших квадратов. Пусть в результате измерений получена таблица некоторой зависимости f: Таблица 1.
Поставим задачу так, чтобы с самого начала обязательно учитывался характер исходной функции: найти функцию заданного вида 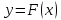 , (1) , (1)которая в точках 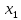 , , 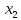 , …, , …, 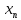 принимает значения как можно более близкие к табличными значениям принимает значения как можно более близкие к табличными значениям 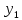 , , 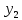 , …, , …, 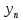 . .Вид приближающей функции F можно определить следующим образом. По таблице 1 строится точечный график функции f, а затем проводится плавная кривая, по возможности наилучшим образом отражающая характер расположения точек (см. рис.1). По полученной таким образом кривой устанавливается вид приближающей функции.   Рис.1. Формулу (1) называют эмпирической формулой или уравнением регрессии y на x. Пусть приближающая функция F в точках 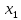 , , 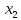 , …, , …, 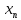 имеет значения: имеет значения: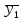 , , 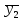 , …, , …, 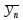 . (2) . (2)Требование близости табличных значений 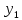 , , 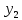 , …, , …, 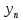 и значений (2) можно истолковать следующим образом. Будем рассматривать совокупность значений функции f из таблицы 1 и совокупность (2) как координаты двух точек n-мерного пространства. С учётом этого задача приближения функции может быть переформулирована следующим образом: найти такую функцию F заданного вида, чтобы расстояние между точками M( и значений (2) можно истолковать следующим образом. Будем рассматривать совокупность значений функции f из таблицы 1 и совокупность (2) как координаты двух точек n-мерного пространства. С учётом этого задача приближения функции может быть переформулирована следующим образом: найти такую функцию F заданного вида, чтобы расстояние между точками M(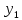 , , 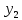 , …, , …, 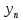 ) и ) и 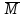 ( (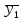 , , 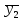 , …, , …, 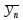 ) было наименьшим. Воспользовавшись метрикой евклидова пространства, приходим к требованию, что величина ) было наименьшим. Воспользовавшись метрикой евклидова пространства, приходим к требованию, что величина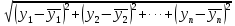 (3) (3)было наименьшей, что равносильно следующему: сумма квадратов  (4) (4)должна быть наименьшей. Итак, задача приближения функции f теперь формулируется следующим образом: для функции f, заданной таблицей 1, найти функцию F определённого вида так, чтобы сумма квадратов (4) была наименьшей. Эта задача носит название приближения функции методом наименьших квадратов. В качестве приближающих функций в зависимости от характера точечного графика функции f часто используют следующие функции: 1)  , ,2) 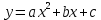 , ,3) 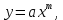 4) 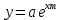 , ,5) 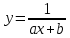 , ,6) 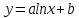 , ,7) 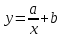 , ,8) 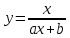 . .Здесь a, b, c, m – параметры. Когда вид приближающей функции установлен, задача сводится только к отысканию значений параметров. 2. Нахождение приближающей функции в виде линейной функции и квадратного трёхчлена (линейная и квадратная регрессии). Будем искать приближающую функцию в виде: 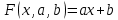 . (5) . (5)Сумма квадратов разностей соответствующих значений функций f и F будет иметь вид: 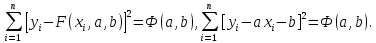 Задача сводится к отысканию её минимума. Используем необходимое условие экстремума: 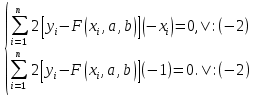 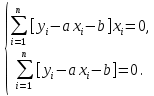 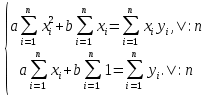 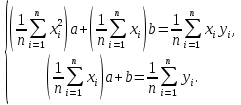 (6) (6)Решив систему (6), получим значения параметров a и b, а следовательно, и конкретный вид линейной функции (5). В случае нахождения приближающей функции в виде квадратного трёхчлена имеем: 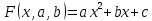 (7) (7)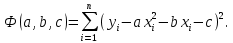 Находим 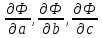 и приравниваем их к нулю: и приравниваем их к нулю: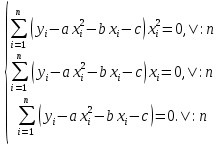 После преобразований получим: 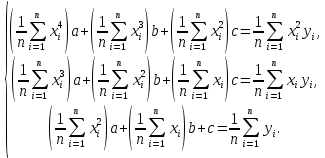 (8) (8)Решение системы (8) даёт значения параметров a, b, c для приближающей функции (7). 3. Нахождение приближающей функции в виде других элементарных функций. Покажем, как нахождение приближающей функции с двумя параметрами F(x, a, b) в виде элементарных функций 1)-8) может быть сведено к нахождению параметров линейной функции. 3.1. Будем искать приближающую функцию в виде:  . (9) . (9)Учитывая, что в исходной таблице 1 значения аргумента и значения функции положительны, прологарифмируем равенство (9) при условии 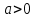 : :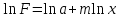 . (10) . (10)Так как F является приближающей для f, функция 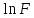 будет приближающей для будет приближающей для 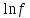 . Введём новую переменную . Введём новую переменную  ; тогда, как следует из (10), ; тогда, как следует из (10), 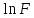 будет функцией от будет функцией от 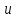 . . 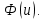 Обозначим 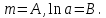 (11) (11)Теперь (10) принимает вид: 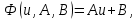 (12) (12)т.е. задача свелась к отысканию приближающей функции в виде линейной. Для нахождения приближающей функции в виде степенной (при сделанных выше предположениях) необходимо выполнить следующее: 1) по данной таблице 1 составить новую таблицу, прологарифмировав значения x и y в исходной таблице; 2) по новой таблице найти параметры A и B приближающей функции вида (12); 3) используя обозначения (11), найти значения параметров a и m, и подставить их в (9). Замечание. Значение разностей 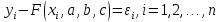 (А) (А)называется отклонениями измеренных значений y от вычисленных по формуле 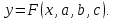 (Б) (Б)Для найденной эмпирической функции (Б) в соответствие с исходной таблицей 1 можно найти сумму квадратов отклонения  (В) (В)Которая в соответствие с принципом наименьших квадратов для заданного вида приближающей функции (и найденных значений параметров a, b, c) должна быть наименьшей. Из двух разных приближений одной и той же табличной формулы, следуя принципу наименьших квадратов, лучшим нужно считать то, для которого сумма (В) имеет наименьшее значение. Результаты выполнения работы 1. 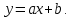 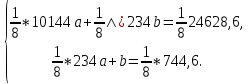  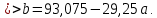 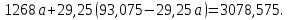 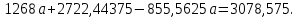 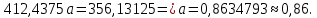 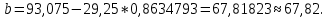  y 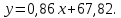  х  Рис.2. 2.  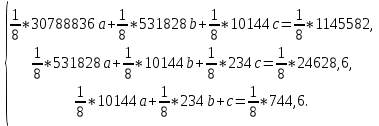 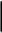 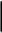 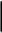 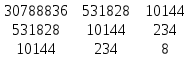 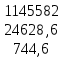   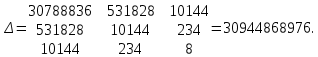 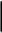     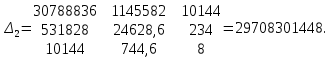  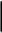 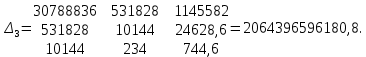 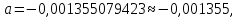 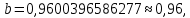 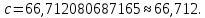  y   х 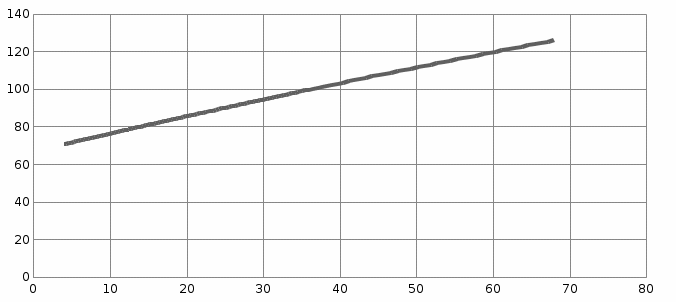 Рис.3. 3. 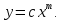 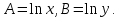
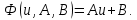 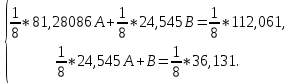 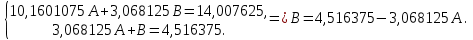 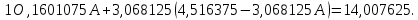 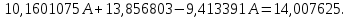 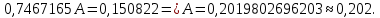 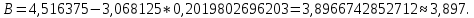 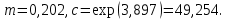  y 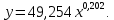  х 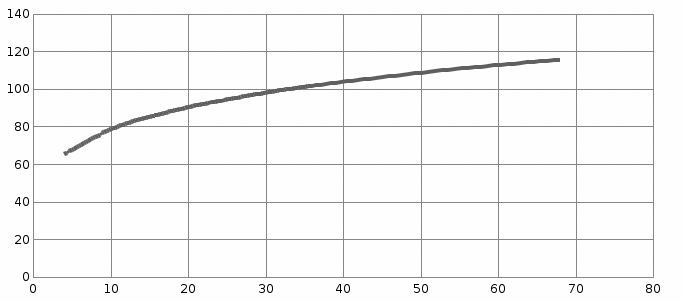 Рис.4.  y 4. Объединим для наглядности графики всех функций.  х 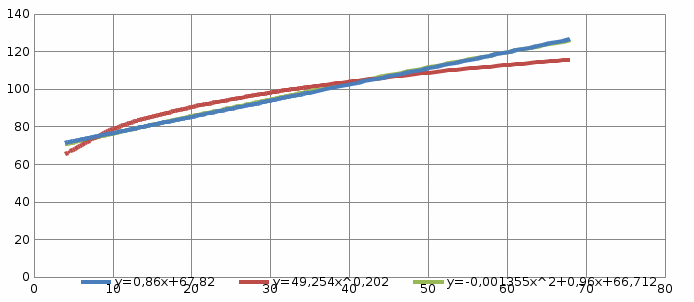 Рис.5. 5. Для сравнения качества приближений вычислим суммы квадратов уклонений.
Как следует из таблицы, сумма квадратов уклонений для линейной функции – 5,6592, для степенной – 224,968, для квадратного трёхчлена – 3,383. Сравнивая качество приближений, находим, что приближение в виде квадратного трёхчлена в данном случае предпочтительнее. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||