экзамен по мат.логике. Трипузова К.Д., 3.031.1.18, МО. Экзаменационный билет номер 29. Трипузова Карина Дмитриевна
 Скачать 22.89 Kb. Скачать 22.89 Kb.
|
|
Экзаменационный билет номер 29. Трипузова Карина Дмитриевна. Формулы F1 и F2 называются равносильными, если их эквиваленция – тавтология. Равносильные преобразования в логике высказываний Замену одной формулы другой ей равносильной будем называть равносильным преобразованием данной формулы. Упрощение формулы уменьшает число высказывательных переменных или знаков операций (минимизация). Логическая равносильность, законы логики. Равносильность – это отношение между формулами и как отношение обладает свойствами рефлексивности, симметричности, транзинтивности. Равносильности логики высказываний называют законами логики. Основные законы логики и основные тавтологии: законы Аристотеля, де Моргана, идемпотентности. Равносильные преобразования в логике высказываний: Логическая равносильность, законы логики; Равносильные преобразования в логике высказываний; Преобразование форм представления формул логики высказываний; Проблема дедукции в логике высказываний. Для замены операции эквивалентности существует два правила: 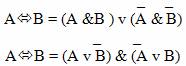 Заменить операцию импликации можно в соответствии со следующим правилом:: A → B = ¬A \/ B Логический вывод — это рассуждение, в ходе которого осуществляется переход от исходного суждения (высказывания или системы высказываний) с помощью логических правил к заключению — новому суждению (высказыванию или системе высказываний). Доказательство (в широком смысле этого слова) — это логическое действие, в процессе которого истинность какого-либо суждения обосновывается с помощью других суждений. Любое неформальное рассуждение (доказательство) представляет собой конечную последовательность повествовательных предложений (то есть высказываний), приводимых в обоснование того, что последнее повествовательное предложение (высказывание) в этой последовательности может быть выведено из начальных повествовательных предложений (высказываний). Чтобы показать некоторое положение, мы должны на что-то сослаться, взять нечто в качестве основы, которая не доказывается, а по договоренности принимается на веру. Такая основа и есть суть аксиом. Однако при этом все последующее уже должно выводиться из аксиом. Следует отметить, что построение аксиоматики теории - дело тонкое, способное приводить к неожиданными и неочевидными результатам и последствиям. Доказательство контрпримером: Многие математические гипотезы имеют в своей основе форму: "Все объекты со свойством А обладают свойством В". Или, используя квантор всеобщности и функцию условного высказывания: x [ А(х) В(х) ], где А(х) - "х имеет свойство А", В(х) - имеет свойство В". Если число возможных значений х является конечным, то в принципе доказательство может быть проведено методом переборов, то есть непосредственной проверкой выполнимости гипотезы для каждого объекта. И в случае, если число объектов не является конечным, то такой возможности не существует даже в принципе. Однако для доказательства несостоятельности гипотезы достаточно привести хотя бы один пример (контрпример), для которого гипотеза не выполнима. Пример 1: Докажите или опровергните высказывание: "для всех положительных целых чисел n, f(n) = n2 - n + 17 - простое число". Доказательство: проверим истинность высказывания для некоторых чисел: f(l) = 17, f(2) = 19, f(3) = 23, f(4) = 29, f(5) = 37. Казалось бы все верно, однако нетрудно заметить, что при n = 17 высказывание принимает значение "ложь": f(17) = 172 - 17 + 17 = 17·17. Пример 2: Справедливо ли утверждение: «если диагонали четырехугольника перпендикулярны, то это ромб?» Доказательство: Построим контрпример. На рисунке изображен четырехугольник, диагонали которого перпендикулярны, но который не является ромбом. Существование такого объекта доказывает ложность исходного утверждения. 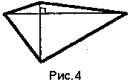 Пример 3: Исследовать, является ли общезначимой формула xP(x) xQ(x) x(P(x) Q(x)) . Доказательство: Предположим, что формула общезначима. Тогда она тождественно истинная для любой области. Приведем контрпример. Положим Q(x) P(x) , оба не тождественно истинные. Тогда x(P(x) P(x)) x1 1 – тождественно истинное высказывание, xP(x) xP(x) 0 0 0 – тождественно ложное высказывание. Правая и левая части формулы не равны между собой. Это означает, что мы получили противоречие и на данном контрпримере рассматриваемая формула ложна. Следовательно, наше предположение об общезначимости было неверным. Значит, рассматриваемая формула не является общезначимой. |
