Лабораторная работа 5 Моделирование простейших логических схем Выполнила студент группы биб2102 Сарачев Данил Вариант 14 Проверил
 Скачать 216.33 Kb.
|
|
Федеральное агентство связи ордена Трудового Красного Знамени Федеральное государственное бюджетное образовательное учреждение высшего образования Московский технический университет связи и информатики Кафедра «Информатика» Лабораторная работа №5 Моделирование простейших логических схем Выполнила студент группы БИБ2102 Сарачев Данил Вариант №14 Проверил проф. Семин В.Г. Москва, 2022 Сформированный вариант задания студентаТаблица истинности для задания определяется датой дня рождения студента. Для этого необходимо дату представить в формате 15.11.03 (ДД:ММ:Гг). Десятилетие Г исключается (просто откидывается). В результате получаем 15113 (ДДММг). Полученное число нужно перевести в двоичный формат представления данных. Результат необходимо дополнить до 16 разрядов дописав перед числом необходимое количество нулей. Таким образом получим 0011 1011 0000 1001 – результирующая логическая функция. По ней составим таблицу истинности и представим в таблице 1. Таблица 1 – Таблица истинности
Задание 1Реализовать полученную функцию на логических элементах. В результирующей логической функции количество единиц равно количеству нулей. Поэтому рационально использовать совершенную дизъюнктивную нормальную форму (СДНФ). 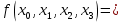  Построим схему реализации на логических элементах (рисунок 1).    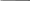   F 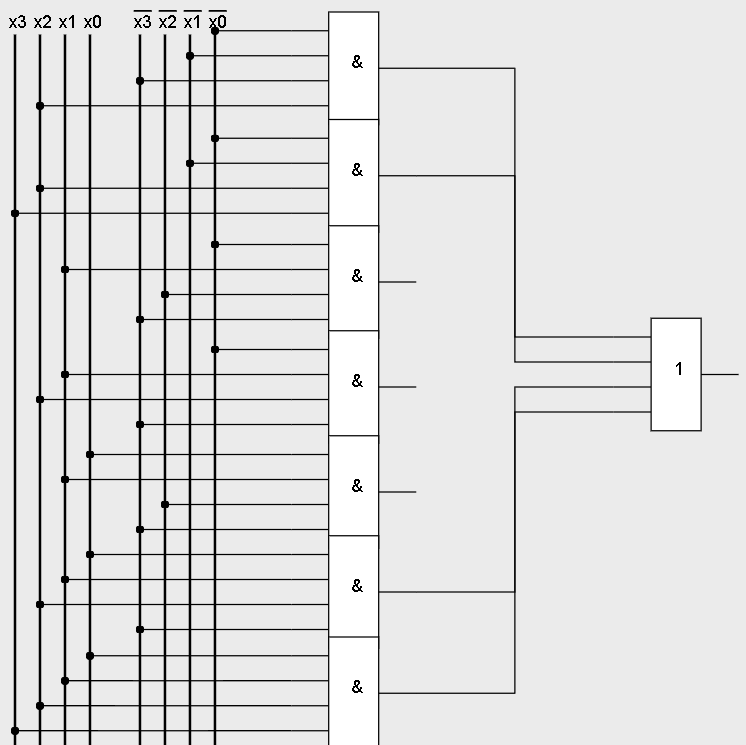 Рисунок 1 – логическая схема задания 1 Задание 3Выполнить минимизацию по карте Карно, синтезировать схему на базисе ИЛИ-НЕ, привести синтезируемую схему, выполнить проверку на соответствие исходной таблице истинности. По карте Карно построим таблицу 2 и составим следующие пары.
Процесс склеивания «1» 1) Количество клеток, входящих в группу, должно быть кратно двум, то есть 2^m, где m=0, 1, 2, 3…. 2) Каждая клетка, входящая в группу, должна иметь m соседних в группе 3) Каждая клетка должна входить в хотя бы одну группу 4) В каждой группе должно быть максимально возможное число клеток 5) Количество групп должно быть минимальным. Считывание СДНФ Считывание функции по группе склеивания производится следующим образом: переменные, которые сохраняют одинаковые значения в клетках группы склеивания, входят в конъюнкцию, причем значениям 1 соответствуют сами переменные, а значениям 0 их отрицания. Первая группа имеет координаты 0111,0110,0011 и 0010 , в этой группе 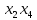 меняют свое значение, следовательно, он исчезает и получается: 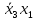 Вторая группа имеет координаты 0111 и 1111,  в этой группе 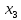 меняют свое значение, следовательно, он исчезает и получается: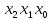 Третья группа имеет координаты 0100 и 0110 в этой группе 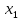 меняют свое значение, следовательно, он исчезает и получается: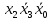 Четвёртая группа имеет координаты 0100 и 1100 в этой группе 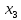меняют свое значение, следовательно, он исчезает и получается::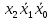 Таким образом, оптимальная минимальная логическая функция имеет следующий вид: 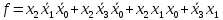 В соответствии с вариантом, переводим в базис И-НЕ, используя законы де Моргана: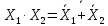 позволяет преобразовать дизъюнкцию в кон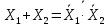ъюнкцию. позволяет преобразовать конъюнкцию в дизъюнкцию.синтезированная схема на базисе ИЛИ-НЕ: 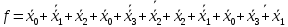  Х0 Построим схему на базисе ИЛИ-НЕ и представим на рисунке 2.      1         1 1    1 1 Х1           1 Х2      1     1  Х3      1 1       1       1 f     1  1     1   Рисунок 2 – Схема на базисе ИЛИ-НЕ задания 3 Проверка: 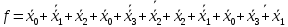 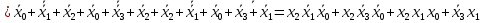Функции совпадают. Построим таблицу истинности по логической схеме на базисе ИЛИ-НЕ:
Таблица истинности по логической схеме на базисе ИЛИ-НЕ абсолютно совпадет с исходной таблицей истинности. |
1
1
1
1