Задания 2. Лабораторная работа 5 Первое начало термодинамики q u a или a dU a идеальный газ

• Название: Лабораторная работа 5 Первое начало термодинамики q u a или a dU a идеальный газ
• Дата: 04.03.2023
• Размер: 375.87 Kb.
• Имя файла: Задания 2.docx
• Тип: Лабораторная работа; #967998

Лабораторная работа №5

Первое начало термодинамики:

Q = U + A или A = dU + A

Идеальный газ – газ, молекулы которого не взаимодеиствуют друг сдругом и их размеры пренебрежимо малы.

Уравнение состояния идеального газа:

PV = RT m/, где

R – универсальная газовая постоянная;

– молярная масса данного газа.

Теплоемкость: C0 = Q/dT

Эксперементальная часть:

1 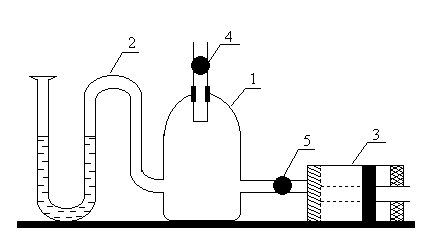– сосуд;

2 – колена манометра;

3 – насос;

4,5 – краны.

Расчеты основных величин.

Таблица измерений:

№ опыта	, мм	, мм	, мм	, мм	, мм	, мм
	240	60	180	175	125	50	1,38
	230	70	160	170	130	40	1,34
	225	75	150	170	130	40	1,36
	280	20	260	185	115	70	1,37
	255	45	210	180	120	60	1,40
	250	50	200	175	125	50	1,34
	235	65	170	175	125	50	1,42
	220	80	140	170	130	40	1,40
	235	65	170	175	125	50	1,42
	225	75	150	170	130	40	1,36

1.     

   

 

 

 



2. Пусть воздух - двухатомный газ (считаем связь между атомами жесткой), т.е. i=5, откуда





Расчет погрешностей.

 

Количество повторений – 10.

Коэффициент Стьюдента:   при P=95%.

0,02



^{Результат :}  

Вывод:в ходе работы был изучен метод Клемана-Дезорма, позволяющий экспериментальным путем определять показатель адиабаты воздуха. Полученный показатель адиабаты (_эксп=1,38) незначительно отличается от теоретического (_теор=1,4), т.к. в состав воздуха входят газы, молекулы которых состоят из различного количества атомов, а показатель _теор был рассчитан для воздуха как для двухатомного газа. Другой причиной различия между полученным результатом и теоретическим является то, что при расчете _теорвоздух считали двухатомным идеальным газом, размерами молекул и их взаимодействиями мы пренебрегали. В реальной жизни воздух - смесь различных газов (O₂, N₂, CO₂ и др. ) и водяного пара.

Лабораторная работа №6

Коэффициент пропорциональности  , называемый коэффициентомдинамической вязкости(или простовязкостью жидкости), зависит от природы и состояния жидкости и с повышением температуры обычно уменьшается.

За единицу вязкости в международной системе единиц СИ принимается 1 Па^.с– это вязкость такой среды, в которой при градиенте скорости между слоями жидкости равном1с^-1и площадью слоя в1м², действует сила трения между этими слоями жидкости1 Ньютон.

,  . (1)

У большинства жидкостей (вода, низкомолекулярные органические соединения, расплавленные металлы и их соли и др.) коэффициент вязкости зависит только от природы жидкости и температуры. Такие жидкости называются ньютоновскими. У некоторых жидкостей, преимущественно высокомолекулярных (например, растворы полимеров) или представляющих дисперсные системы (суспензии и эмульсии), коэффициент вязкости зависит также от режима течения (давления, градиента скорости и т.д.). Такие жидкости называютненьютоновскимиилиструктурно – вязкими. Их вязкость характеризуют так называемымусловным коэффициентом вязкости, который относится к определенным условиям течения жидкости (давление, градиент скорости).

Кровь представляет суспензию форменных элементов в белковом растворе – плазме и является неньютоновской жидкостью. Кроме того, при течении крови по многим сосудам наблюдается концентрация форменных элементов в центральной части потока, где вязкость соответственно увеличивается. В ряде случаев при анализе гемодинамики считают коэффициент вязкости крови приблизительно постоянной средней величиной по всему сечению кровеносного сосуда.

Относительная вязкость крови (относительно дистиллированной воды) в норме составляет 4,2 – 6. При патологии она может снижаться, например, до 2 – 3 при анемии или повышаться до 15 – 20 при полицитемии. Относительная вязкость сыворотки крови в норме составляет 1,64 – 1,69, а при различных видах патологии обычно находится в пределах 1,5 – 2,0.

В данной лабораторной работе экспериментально изучается ряд методов определения коэффициента вязкости жидкостей.

Рассмотрим некоторые методы определения коэффициента вязкости жидкости.

1. Определение коэффициента вязкости жидкостей капиллярным вискозиметром

Методика измерения вязкости капиллярным вискозиметром основана на уравнении Пуазейля:

, (2)

где  – объем жидкости, протекающей через капилляр за время , - радиус, а – длина капилляра, - градиент давления;  и - давление в начале и в конце капилляра

( > ).

Непосредственное определение коэффициента вязкости по этой формуле встречает серьезные экспериментальные трудности, т.к. радиус капилляра  входит в формулу в четвертой степени и погрешность при измерении радиуса значительно снижает точность экспериментальных данных. Поэтому вместо непосредственного определения коэффициента вязкости по формуле (2) пользуются сравнительным методом. Для этого берут поочередно две жидкости и измеряют время истечения одинаковых объемов каждой жидкости через один и тот же капилляр. Тогда для первой жидкости можно записать:

(3)

аналогично для второй жидкости

. (4)

Поскольку  , то можно найти из этого условия коэффициент вязкости второй жидкости:

. (5)

В нашем опыте жидкость вытекает под действием силы тяжести поэтому, с учетом того, что давление столба жидкости  получим:

,

где  и  – плотности первой и второй жидкости. Тогда формула (5) примет вид:

. (6)

Таким образом, зная время истечения вязких жидкостей, их плотности и коэффициент вязкости одной из них, можно найти вязкость другой жидкости. В качестве жидкости с известным коэффициентом вязкости обычно берут дистиллированную воду.

Капиллярный вискозиметр представляет собой капилляр, заканчивающийся сверху резервуаром. Под резервуаром и над ним (рис.2) нанесены две метки (АиВ), ограничивающие определенный объем жидкости, время истечения которого определяется на опыте. Для исключения влияния сил поверхностного натяжения нижний конец капилляра погружают в исследуемую жидкость на 5–6 мм. Резиновой грушей или другим способом осторожно засасывают жидкость в резервуар и наполняют его выше верхней метки «В». Затем дают жидкости возможность свободно вытекать и, при достижении уровнем жидкости верхней метки, включают секундомер. Останавливают секундомер при похождении уровня жидкости через нижнюю метку.

Р ис. 2.

Этим методом непосредственно можно определить относительную вязкость, т.е. во сколько раз отличается вязкость исследуемой жидкости от вязкости эталонной жидкости.

Метод определение вязкости жидкости с помощью медицинского вискозиметра основан на том, что согласно формуле Пуазейля объем вязкой жидкости, протекающей по капилляру за определенный промежуток времени, при прочих равных условиях (в частности, при одинаковых радиусах капилляров, разностях давлений на концах капилляров) обратно пропорционально коэффициенту вязкости жидкости. Следовательно, для двух сравниваемых жидкостей можно записать:

_{k и ,}

где l – длина капилляраа иб (рис.3), тогда получим: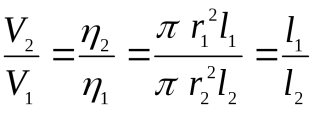

(если r₁ = r₂ ). (7)

Из этой формулы видно, что пути l₁ иl₂, проходимые эталонной и исследуемой жидкостью в капиллярных трубкахАиБ(рис.3) одинакового сечения, обратно пропорциональны их коэффициентам вязкости 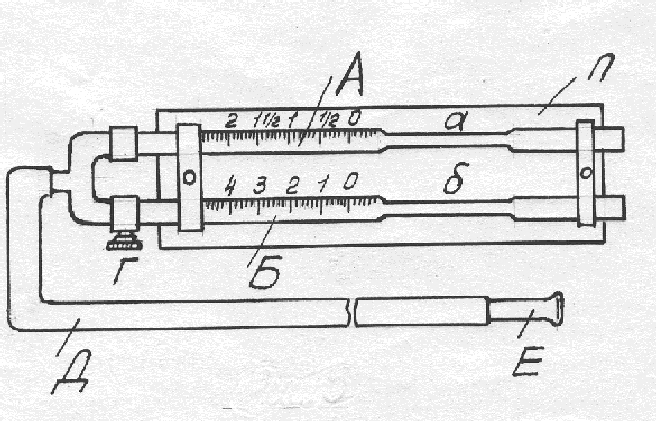 и . Зная значение  и, измерив соотношение - относительную вязкость, можно найти коэффициент вязкости исследуемой жидкости по формуле:

= k  .

Рис. 3.

Медицинский вискозиметр

Применяемый в клинике прибор для определения вязкости крови, состоит из двух градуированных пипеток АиБ, закрепленных на общей подставкеП(рис. 3). В средней части пипеток имеются одинаковые капиллярыаибдлиной l. Слева концы пипеток соединены тройником, от которого идет резиновая трубкаДсо стеклянным наконечникомЕ. Нижняя пипетка имеет слева кранГ. При работе, открыв кранГи втягивая ртом воздух через наконечникЕ, заполняют пипеткуБдистиллированной водой до метки «0». Затем, закрыв кранГ, аналогичным образом наполняют до такого же уровня пипеткуА исследуемой жидкостью и кладут прибор горизонтально.

Далее открывают кран Ги, втягивая ртом или другим способом воздух (создавая в двух капиллярах одинаковую разность давленийР₁ -Р₂), всасывают жидкость из обеих пипеток так, чтобы исследуемая жидкость дошла до цифры 1 (l₂=1). При этом вода, как менее вязкая жидкость, дойдет до более высокой цифры (l₁ = k), которая и укажет относительную вязкостьn:

.

Вязкость исследуемой жидкости  = k , где  – вязкость воды при данной температуре (табл.3).

3. Определение коэффициента вязкости жидкостей методом Стокса

При наличии больших количеств жидкости коэффициент вязкости может быть определен методом Стокса.

Преимущество этого метода по сравнению с капиллярным заключается в том, что измерения могут быть выполнены в закрытом сосуде – обстоятельство, важное для физиологов и медиков. По данному методу в исследуемую жидкость опускают шарик небольших размеров. При движении шарика слой жидкости, граничащий с его поверхностью, прилипает к шарику и движется со скоростью шарика. Ближайшие смежные слои жидкости также приводятся в движение, но получаемая ими скорость тем меньше, чем дальше они находятся от шарика.

Стокс установил, что при не слишком быстром движении тела сферической формы в вязкой жидкости сила сопротивления движению  прямо пропорциональна скорости  , радиусу телаr и коэффициенту вязкости жидкости  . На шарик в вязкой жидкости действуют три силы (рис.4):

1. 
   Сила Стокса
   

. (8)

2. 
   Сила тяжести
   

(ρ – плотность шарика). (9)

3. 
   Выталкивающая сила (сила Архимеда)
   

(ρ₁ – плотность жидкости). (10)

По второму закону Ньютона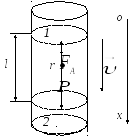

. (11)

Р ис. 4.

Переходя от векторной записи к алгебраической (проектируя уравнение (11) на ось ох) и учитывая направление действия сил, получим:

F_c+F_A - Р= - ma. (11a)

Так как сила трения  зависит от скорости (8), то устанавливается равномерное движение шарика (a=0) и уравнение (11а) принимает следующий вид:

F_c+F_A - Р=0илиР = F_c+F_A . (11б)

Подставляя значения этих сил из формул (8-10) в уравнение (11б), получим:

.

Из последнего уравнения получим:

(12)

Эта формула справедлива для шариков небольшого размера, т.к. в противном случае, при движении шарика в жидкости возникают завихрения, и течение жидкости становится турбулентным.

Таким образом, зная скорость установившегося движения  , плотности шарика и жидкости и , а также радиус шарикаr, можно по формуле (12) вычислить значение коэффициента вязкости исследуемой жидкости. Прибор для измерения состоит, например, из стеклянного цилиндрического сосуда (рис.4), наполненного исследуемой жидкостью, плотность которой известна. На стенке сосуда имеются две горизонтальные метки1и2, расположенные друг от друга на расстоянииl. Диаметр2rшарика измеряют обычно с помощью микрометра или штангенциркуля. Шарик опускают в жидкость по оси цилиндра, причем глаз наблюдателя должен быть при этом установлен против метки так, чтобы вся она сливалась в одну прямую. При прохождении шариком первой метки включают секундомер, при прохождении второй - останавливают. Считая, что к моменту прохождения верхней метки скорость установилась постоянной, получим  , гдеt- время прохождения шарика расстоянияlмежду метками1и2. По формуле (12) вычисляется коэффициент вязкостиηисследуемой жидкости.

По вышеописанному методу можно также определить размеры (радиус r) коллоидной частицы по скорости ее оседания  в монодисперсной системе.

Из формулы (12) следует, что

. (13)

Этот метод играет важную роль в медицине, он дает возможность определить размеры кровяных шариков и других малых частиц по скорости их оседания. А определение скорости оседания эритроцитов (СОЭ) (иногда ее называют реакцией оседания эритроцитов – РОЭ), изменяющейся при воспалительных процессах, является одним из методов диагностики.