ЛР5 ЦОС. Лабораторная работа 5 по дисциплине Цифровая обработка сигналов Синтез кихфильтров методом окон
 Скачать 338.82 Kb. Скачать 338.82 Kb.
|
|
«МОСКОВСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ СВЯЗИ И ИНФОРМАТИКИ» (МТУСИ) Лабораторная работа №5 по дисциплине Цифровая обработка сигналов «Синтез КИХ-фильтров методом окон» Выполнили: бригада №4 студенты гр. БРМ1901 Нагайцева К.А., Хлебнов С.Д. Проверила : Шубина М.В. Москва 2021 Цель работыИзучить процедуру синтеза КИХ-фильтров методом окон и овладеть программными средствами MATLAB для синтеза и анализа КИХ-фильтров; познакомиться с GUI WinTool (Window Design and Analysis Tool – средство создания и анализа окон) и GUI FVTool (Filter Visualization Tool – средство визуализации фильтра). Исходные данныеТаблица 1. Требования к АЧХ ФНЧ
Таблица 2. Требования к АЧХ ФВЧ
Таблица 3. Требования к АЧХ ПФ
Таблица 4. Требования к АЧХ РФ
Выполнение:АЧХ ФНЧ% ЛР №5. СИНТЕЗ КИХ-ФИЛЬТРА ФНЧ МЕТОДОМ ОКОН % % п.1. ВВОД ТРЕБОВАНИЙ К АЧХ ФНЧ % % Введите НОМЕР БРИГАДЫ и ТРЕБОВАНИЯ к АЧХ Nb = 4 Fs = 5400 ft = 620 fk = 890 d1 = 0.05 d2 = 0.01 % Проверьте ПРАВИЛЬНОСТЬ ввода ИСХОДНЫХ ДАННЫХ % При ПРАВИЛЬНЫХ ИСХОДНЫХ ДАННЫХ введите 1 % При НЕПРАВИЛЬНЫХ ИСХОДНЫХ ДАННЫХ введите 0 и ПОВТОРИТЕ ввод --> % % Для продолжения нажмите % % п.2. ВЫЧИСЛЕНИЕ ПАРАМЕТРОВ ФУНКЦИИ kaiserord % % Для вывода параметров функции kaiserord нажмите R = 45 wc = 0.27963 beta = 3.3953 ftype = low % % Для продолжения нажмите % % п.3. СИНТЕЗ КИХ-ФИЛЬТРА ФНЧ % % Для синтеза КИХ-фильтра ФНЧ нажмите % Синтезирован КИХ-фильтр ФНЧ порядка R = 45 % % Для вывода ФАКТИЧЕСКИХ максимальных отклонений АЧХ % в ПП (dp) и ПЗ (ds) и ЗАДАННЫХ отклонений d1 и d2 нажмите % dp = 0.010054 ds = 0.0094564 d1 = 0.05 d2 = 0.01 % % Сравните ФАКТИЧЕСКИЕ отклонения с ЗАДАННЫМИ % % Если ПОРЯДОК соответствует МИНИМАЛЬНОМУ, введите 1 % Если НЕ соответствует, введите 0 и затем ПОРЯДОК R --> % Синтезирован ФНЧ минимального порядка R = 45 % % Для продолжения нажмите % % п.4. АНАЛИЗ ХАРАКТЕРИСТИК КИХ-ФИЛЬТРА ФНЧ % % Для вывода ГРАФИКОВ ИХ, АЧХ и ФЧХ нажмите % % Для продолжения нажмите % % п.5. ОПИСАНИЕ СТРУКТУРЫ КИХ-ФИЛЬТРА ФНЧ В ВИДЕ ОБЪЕКТА dfilt % % Для вывода СВОЙСТВ ОБЪЕКТА dfilt нажмите F_lowpass = FilterStructure: 'Direct-Form Symmetric FIR' Arithmetic: 'double' Numerator: [1x46 double] PersistentMemory: false % % СИНТЕЗ КИХ-ФИЛЬТРА ФНЧ ЗАВЕРШЕН 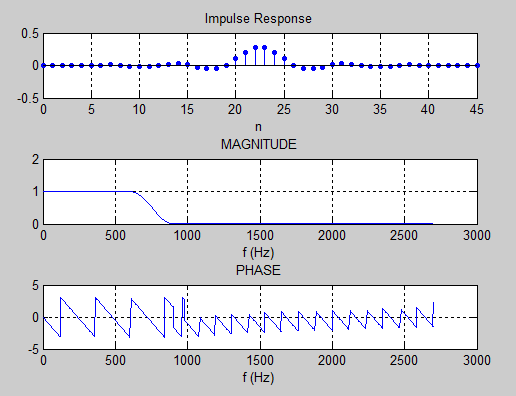 Рисунок 1 - Синтез КИХ-фильтра низких частот (ФНЧ) АЧХ ФВЧ % ЛР №5. СИНТЕЗ КИХ-ФИЛЬТРА ФВЧ МЕТОДОМ ОКОН % % п.1. ВВОД ТРЕБОВАНИЙ К АЧХ ФВЧ % % Введите НОМЕР БРИГАДЫ и ТРЕБОВАНИЯ к АЧХ Nb = 4 Fs = 5400 fk = 620 ft = 890 d2 = 0.01 d1 = 0.05 % Проверьте ПРАВИЛЬНОСТЬ ввода ИСХОДНЫХ ДАННЫХ % При ПРАВИЛЬНЫХ ИСХОДНЫХ ДАННЫХ введите 1 % При НЕПРАВИЛЬНЫХ ИСХОДНЫХ ДАННЫХ введите 0 и ПОВТОРИТЕ ввод --> % % Для продолжения нажмите % % п.2. ВЫЧИСЛЕНИЕ ПАРАМЕТРОВ ФУНКЦИИ kaiserord % % Для вывода параметров функции kaiserord нажмите R = 46 wc = 0.27963 beta = 3.3953 ftype = high % % Для продолжения нажмите % % п.3. СИНТЕЗ КИХ-ФИЛЬТРА ФВЧ % % Для синтеза КИХ-фильтра ФВЧ нажмите % Синтезирован КИХ-фильтр ФВЧ порядка R = 46 % % Для вывода ФАКТИЧЕСКИХ максимальных отклонений АЧХ % в ПЗ (ds) и ПП (dp) и ЗАДАННЫХ отклонений d2 и d1 нажмите % ds = 0.0086177 dp = 0.0085795 d2 = 0.01 d1 = 0.05 % % Сравните ФАКТИЧЕСКИЕ отклонения с ЗАДАННЫМИ % % Если ПОРЯДОК соответствует МИНИМАЛЬНОМУ, введите 1 % Если НЕ соответствует, введите 0 и затем ПОРЯДОК R --> % Синтезирован ФВЧ минимального порядка R = 46 % % Для продолжения нажмите % % п.4. АНАЛИЗ ХАРАКТЕРИСТИК КИХ-ФИЛЬТРА ФВЧ % % Для вывода ГРАФИКОВ ИХ, АЧХ и ФЧХ нажмите % % Для продолжения нажмите % % п.5. ОПИСАНИЕ СТРУКТУРЫ КИХ-ФИЛЬТРА ФВЧ В ВИДЕ ОБЪЕКТА dfilt % % Для вывода СВОЙСТВ ОБЪЕКТА dfilt нажмите F_highpass = FilterStructure: 'Direct-Form Symmetric FIR' Arithmetic: 'double' Numerator: [1x47 double] PersistentMemory: false % % СИНТЕЗ КИХ-ФИЛЬТРА ФВЧ ЗАВЕРШЕН 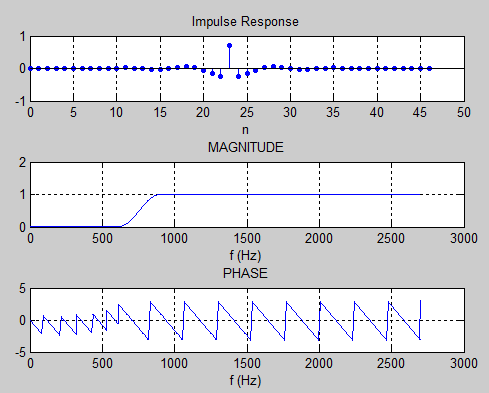 Рисунок 2 - Синтез КИХ-фильтра верхних частот (ФВЧ) АЧХ ПФ Nb = 4 Fs = 5400 fk1 = 350 ft1 = 620 ft2 = 1450 fk2 = 1720 d21 = 0.01 d1 = 0.05 d22 = 0.01 % Проверьте ПРАВИЛЬНОСТЬ ввода ИСХОДНЫХ ДАННЫХ % При ПРАВИЛЬНЫХ ИСХОДНЫХ ДАННЫХ введите 1 % При НЕПРАВИЛЬНЫХ ИСХОДНЫХ ДАННЫХ введите 0 и ПОВТОРИТЕ ввод --> % % Для продолжения нажмите % % п.2. ВЫЧИСЛЕНИЕ ПАРАМЕТРОВ ФУНКЦИИ kaiserord % % Для вывода параметров функции kaiserord нажмите R = 45 wc(1) = 0.17963 wc(2) = 0.58704 beta = 3.3953 ftype = DC-0 % % Для продолжения нажмите % % п.3. СИНТЕЗ КИХ-ФИЛЬТРА ПФ % % Для синтеза КИХ-фильтра ПФ нажмите % Синтезирован КИХ-фильтр ПФ порядка R = 45 % % Для вывода ФАКТИЧЕСКИХ максимальных отклонений АЧХ % в ПЗ1 (ds1), ПП (dp) и ПЗ2 (ds2) и ЗАДАННЫХ отклонений d21, d1 и d22 нажмите % ds1=0.0097705 dp = 0.01166 ds2 = 0.0086559 d21 = 0.01 d1 = 0.05 d22 = 0.01 % % Сравните ФАКТИЧЕСКИЕ отклонения с ЗАДАННЫМИ % % Если ПОРЯДОК соответствует МИНИМАЛЬНОМУ, введите 1 % Если НЕ соответствует, введите 0 и затем ПОРЯДОК R --> % Синтезирован ПФ минимального порядка R = 45 % % Для продолжения нажмите % % п.4. АНАЛИЗ ХАРАКТЕРИСТИК КИХ-ФИЛЬТРА ПФ % % Для вывода ГРАФИКОВ ИХ, АЧХ и ФЧХ нажмите % % Для продолжения нажмите % % п.5. ОПИСАНИЕ СТРУКТУРЫ КИХ-ФИЛЬТРА ПФ В ВИДЕ ОБЪЕКТА dfilt % % Для вывода СВОЙСТВ ОБЪЕКТА dfilt нажмите F_bandpass = FilterStructure: 'Direct-Form Symmetric FIR' Arithmetic: 'double' Numerator: [1x46 double] PersistentMemory: false % % СИНТЕЗ КИХ-ФИЛЬТРА ПФ ЗАВЕРШЕН 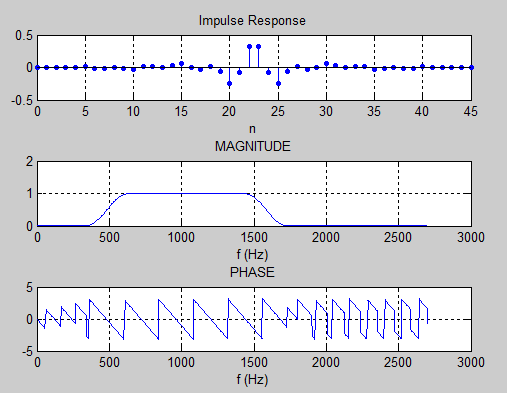 Рисунок 3 - Синтез полосового КИХ-фильтра (ПФ) АЧХ РФ % ЛР №5. СИНТЕЗ КИХ-ФИЛЬТРА РФ МЕТОДОМ ОКОН % % п.1. ВВОД ТРЕБОВАНИЙ К АЧХ РФ % % Введите НОМЕР БРИГАДЫ и ТРЕБОВАНИЯ к АЧХ Nb = 4 Fs = 5400 ft1 = 350 fk1 = 620 fk2 = 1450 ft2 = 1720 d11 = 0.05 d2 = 0.01 d12 = 0.05 % Проверьте ПРАВИЛЬНОСТЬ ввода ИСХОДНЫХ ДАННЫХ % При ПРАВИЛЬНЫХ ИСХОДНЫХ ДАННЫХ введите 1 % При НЕПРАВИЛЬНЫХ ИСХОДНЫХ ДАННЫХ введите 0 и ПОВТОРИТЕ ввод --> % % Для продолжения нажмите % % п.2. ВЫЧИСЛЕНИЕ ПАРАМЕТРОВ ФУНКЦИИ kaiserord % % Для вывода параметров функции kaiserord нажмите R = 46 wc(1) = 0.17963 wc(2) = 0.58704 beta = 3.3953 ftype = stop % % Для продолжения нажмите % % п.3. СИНТЕЗ КИХ-ФИЛЬТРА РФ % % Для синтеза КИХ-фильтра РФ нажмите % Синтезирован КИХ-фильтр РФ порядка R = 46 % % Для вывода ФАКТИЧЕСКИХ максимальных отклонений АЧХ % в ПП1 (dp1), ПЗ (ds) и ПП2 (dp2) и ЗАДАННЫХ отклонений d11, d2 и d12 нажмите % dp1=0.0093706 ds = 0.008525 dp2 = 0.0072282 d11 = 0.05 d2 = 0.01 d12 = 0.05 % % Сравните ФАКТИЧЕСКИЕ отклонения с ЗАДАННЫМИ % % Если ПОРЯДОК соответствует МИНИМАЛЬНОМУ, введите 1 % Если НЕ соответствует, введите 0 и затем ПОРЯДОК R --> % Синтезирован РФ минимального порядка R = 46 % % Для продолжения нажмите % % п.4. АНАЛИЗ ХАРАКТЕРИСТИК КИХ-ФИЛЬТРА РФ % % Для вывода ГРАФИКОВ ИХ, АЧХ и ФЧХ нажмите % % Для продолжения нажмите % % п.5. ОПИСАНИЕ СТРУКТУРЫ КИХ-ФИЛЬТРА РФ В ВИДЕ ОБЪЕКТА dfilt % % Для вывода СВОЙСТВ ОБЪЕКТА dfilt нажмите F_bandstop = FilterStructure: 'Direct-Form Symmetric FIR' Arithmetic: 'double' Numerator: [1x47 double] PersistentMemory: false % % СИНТЕЗ КИХ-ФИЛЬТРА РФ ЗАВЕРШЕН 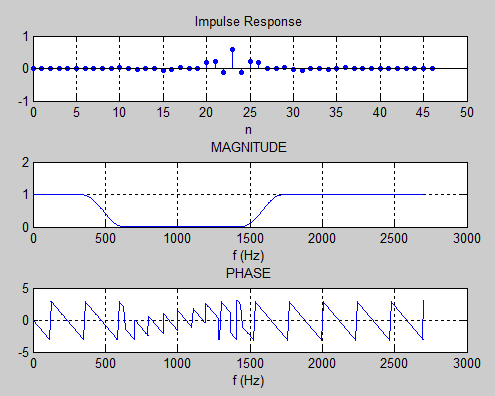 Рисунок 4 – Синтез режекторного КИХ-фильтра (РФ)
Вывод: В результате работы я изучила процедуру синтеза КИХ-фильтров методом окон и овладела программными средствами MATLAB для синтеза и анализа КИХ-фильтров. С помощью рассчитанных входных данных (частота дискретизации, граничные частоты и допустимые отклонения) и программных средств MATLAB мною были синтезированы КИХ-фильтры (ФНЧ, ФВЧ, ПФ, РФ). Для каждого фильтра были построены графики: ИХ, АЧХ и ФНЧ. Контрольные вопросы: Дайте определение цифрового фильтра. Цифровой фильтр - любой фильтр, обрабатывающий цифровой сигнал с целью выделения и/или подавления определённых частот этого сигнала. В общем случае термином цифровой фильтр называют аппаратную или программную реализацию математического алгоритма, входом которого является цифровой сигнал, а выходом - другой цифровой сигнал с определенным образом модифицированной формой и/или амплитудной и фазовой характеристикой. Перечислите основные этапы проектирования цифрового фильтра. Этапы разработки ЦФ Определение требований к фильтру или составление спецификации требований Вычисление коэффициента цифрового фильтра Представление цифрового фильтра подходящей вычислительной структуры Анализ влияния конечной разрядности на работу фильтра Реализация ЦФ на программном и/или аппаратном уровне Запишите передаточную функцию КИХ-фильтра. Дайте определение длины и порядка КИХ-фильтра. ДлинаКИХ-фильтра — количество коэффициентов передаточной функции N. ПорядокКИХ-фильтра — порядок передаточной функции R = N-1. Назовите основные особенности КИХ-фильтров. Основная особенность фильтра является ограниченность во времени его импульсной характеристики, то есть с определенного момента времени она становится равной нулю. В каких точках ФЧХ фильтра имеет скачок на π? Скачок ЛФЧХ КИХ-фильтра на π – в нулях АЧХ Назовите признаки, по которым различают четыре типа КИХ-фильтров с ЛФЧХ. Различают типа КИХ-фильтров с ЛФЧХ по следующим двум признакам: четность/нечетность порядка; симметрия/антисимметрия ИХ Какие типы КИХ-фильтров с ЛФЧХ могут использоваться для синтеза фильтра методом окон? Методы синтеза частотно-избирательных КИХ-фильтров изначально предполагают ЛФЧХ (с точностью до скачков на π), поэтому требования задаются только к АЧХ в основной полосе частот [0; fд/2] и включает в себя: ● частоту дискретизации fд; ● граничные частоты полос пропускания (ПП) и полос задерживания (ПЗ), для которых введены условные обозначения: ● fχ – граничная частота ПП для ФНЧ и ФВЧ; ● fk – граничная частота ПЗ для ФНЧ и ФВЧ; ● f-χ , fχ – левая и правая граничные частоты ПП для ПФ и РФ; ● f-k , fk – левая и правая граничные частоты ПЗ для ПФ и РФ; Что входит в требования к АЧХ КИХ-фильтра? Проверка заключается в сравнении фактических максимальных по модулю отклонений АЧХ от идеальной АЧХ в ПП и ПЗ с заданными максимально допустимыми отклонениями. Возможны две ситуации. Требования к АЧХ не выполняются. В этом случае следует увеличить порядок R. Требования к АЧХ выполняются. В этом случае следует уменьшить порядок R. В обоих случаях увеличение/уменьшение порядка R продолжается до тех пор, пока не будет найден минимальный порядок, при котором выполняются требования к АЧХ. Назовите основные свойства АЧХ и ФЧХ. ЧХ H (e jωT ) , АЧХ A(ω) и ФЧХ ϕ(ω) – непрерывные функции частоты по определению. ЧХ H (e jωT ) , АЧХ A(ω) и ФЧХ ϕ(ω) – периодические функции частоты с периодом, равным частоте дискретизации ωд = 2Tπ . Что отображает структура ЦФ и чем определяется ее вид? Структура (структурная схема) ЦФ отображает алгоритм вычисления реакции по разностному уравнению и определяется видом передаточной функции. Назовите основные структуры КИХ-фильтров. Трансверсальная (прямая структура); 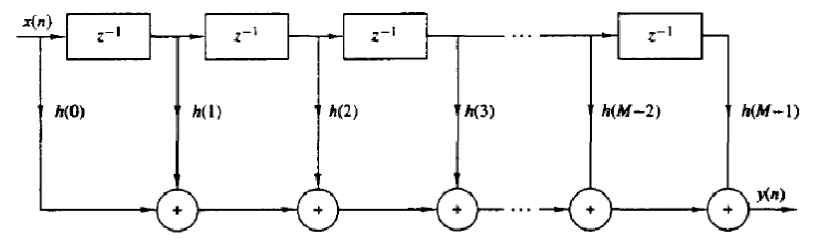 Частотная выборка; 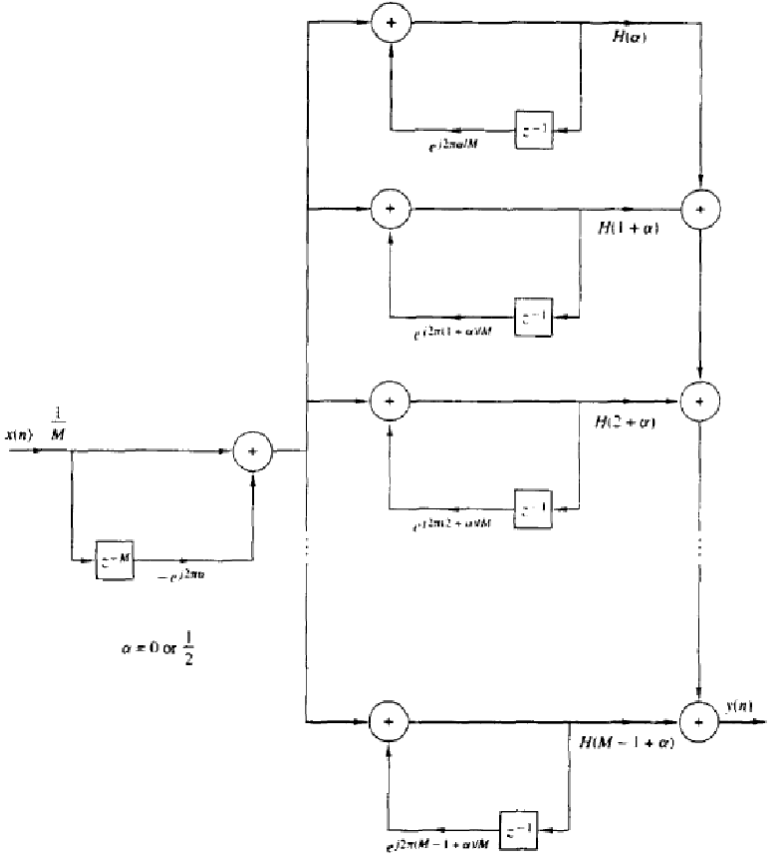 Быстрая свертка; 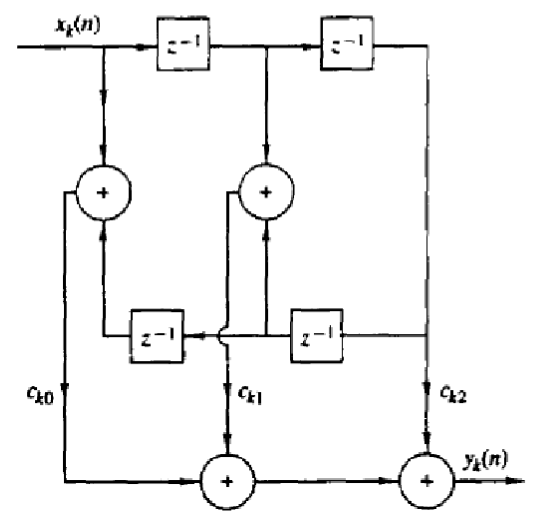 Решетчатая. 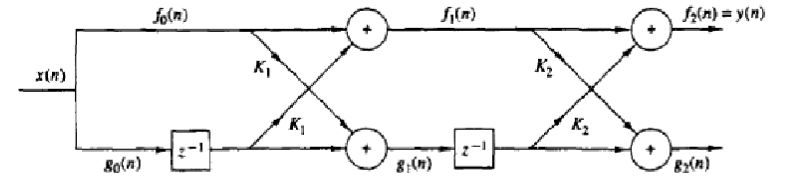 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
