5_Решение НУ (2). Лабораторная работа 5 Решение нелинейных уравнений и систем

• Название: Лабораторная работа 5 Решение нелинейных уравнений и систем
• Анкор: Htitybt
• Дата: 17.02.2023
• Размер: 0.68 Mb.
• Имя файла: 5_Решение НУ (2).doc
• Тип: Лабораторная работа; #941873
• страница: 2 из 2

Нелинейные уравнения и системы в SCILAB

1. Алгебраические уравнения

a₀xⁿ+a₁x^n–1+…+a_n–1x+a_n=0, где a₀≠0, n1,

a_i – коэффициенты алгебраического уравнения n–й степени.

Чтобы решить алгебраическое уравнение в Scilab необходимо:

• 
  определить (задать) полином;
  
• 
  найти его корни.
  

Для определения алгебраического уравнения предназначена функция

poly(a, 'x', ['fl'])

где

a – число или матрица чисел, x – символьная переменная, fl – строковая переменная, определяющая способ задания полинома. Параметр fl принимает два значения 'r' или 'c'. Если fl=c, то формируется полином с коэффициентами, хранящимися в параметре a. Если fl=r, то значения параметра a воспринимаются функцией как корни, для которых необходимо рассчитать коэффициенты соответствующего полинома. По умолчанию fl=r.

Примеры создания полиномов.

-->poly([1 0 2],'x')

ans =

2 3

2x - 3x + x
-->poly([1 0 2],'x','c')

ans =

2

1 + 2x

Для отыскания корней полинома (решения алгебраического уравнения) применяют функцию

roots(p)

где p заданный ранее полином.

ЗАДАЧА 1. Найти корни полинома 2x⁴–8x³+8x²–1=0.

Графическое решение

x=-1:0.2:3; y=-1+8*x^2-8*x^3+2*x^4; plot(x,y); xgrid()



Аналитическое решение

-->V=[-1 0 8 -8 2];

-->p=poly(V,'x','c')

p =

2 3 4

- 1 + 8x - 8x + 2x

-->X=roots(p)

X =

! 0.4588039 !

! - 0.3065630 !

! 1.5411961 !

! 2.306563 !

2. Трансцендентные уравнения

Для решения уравнения отличного от алгебраического f(x)=0 необходимо

• 
  задать функцию f(x), описывающая левую часть уравнения;
  
• 
  найти начальное приближение корня x0;
  
• 
  уточнить начальное приближение численно.
  

Задать функцию в Scilab можно при помощи оператора

deff('[y]=f(x)','y=fun')

где x – входной параметр; y – выходной параметр, то есть переменная, которой будет присвоен конечный результат вычислений; f – имя с которым функция будет вызываться, fun – строка символов, определяющих функцию.

Вычислить приближенное значение корня уравнения f(x)=0 можно, если построить график функции f(x) и найти точки его пересечения с осью ОХ.

Решают заданное уравнение f(x)=0 с помощью функции

fsolve(x0,f),

где x0 – начальное приближение, f – функция, описывающая левую часть уравнения f(x)=0.

ЗАДАЧА 2. Найти корни уравнения f(x)=e^x/5–2(x-1)².

x=-2:0.2:6;

deff('[y]=f(x)', 'y=exp(x)/5-2*(x-1)^2'); plot(x,y)

График функции f(x) трижды пересекает ось абсцисс, то есть уравнение имеет три корня.



Последовательно вызывая функцию fsolve с различными начальными приближениями, получим все решения заданного уравнения.

-->x(1)=fsolve(0,f);

-->x(2)=fsolve(2,f);

-->x(3)=fsolve(5,f);

-->x

x =

! 0.5778406 !

! 1.7638701 !

! 5.1476865 !

Начальные приближения можно задать в виде вектора и тогда функцию можно вызвать один раз.

-->fsolve([0;2;5],f)

ans =

! 0.5778406 !

! 1.7638701 !

! 5.1476865 !

3. Системы уравнений

Для решения систем уравнений в Scilab так же применяют функцию fsolve(x0,f).

ЗАДАЧА 3. Решить систему уравнений:{x₁²+x₂²=1; x₁³–x₂=0}.

x=-1:0.01:1;

y1=(1-x^2)^0.5;

y2=-(1-x^2)^0.5;

y3=x^3;

plot(x,y1,x,y2,x,y3)

Графическое решение системы показывает, что она имеет две пары корней.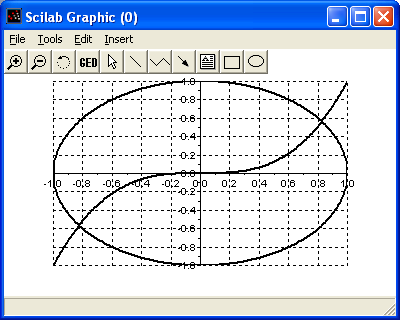



Окружность и гипербола пересекаются в точках [0.8;0.6] и [-0.8;-0.6]. Эти значения приблизительны. Для того чтобы уточнить их, применим функцию fsolve, предварительно определив систему.

deff('[y]=fun(x)', 'y(1)=x(1)^2+x(2)^2-1; y(2)=x(1)^3-x(2)');

fsolve([-0.5 -0.5],fun)

ans =

-0.8260314 - 0.5636242

fsolve([0.5 0.5],fun)

ans =

0.8260314 0.5636242