Отчет ИВТ на АТ. ИВТ на АТ(5-7). Лабораторная работа 5. Решение задач оптимизации с помощью Excel (задача о назначениях)
 Скачать 432.86 Kb. Скачать 432.86 Kb.
|
|
Лабораторная работа №5. Решение задач оптимизации с помощью Excel (задача о назначениях) Цель работы: получение навыков решения задач оптимизации с помощью Excel (задача о назначениях). Задание: стоимость cij выполнения i-м рабочим j-й работы для заданного варианта приведена в таблице 1. Составить план выполнения работ так, чтобы их суммарная стоимость была минимальной. Таблица 1
1. Составим математическую модель. Число рабочих (5) превышает количество операций, которое они должны выполнить (4). Следовательно, вводятся одна фиктивная операция – 5, время на выполнение которых равно нулю, т. к. они фактически не выполняются. В ячейки, в которых был знак «минус», вместо него помещены числа, существенно превышающие другие затраты времени (1000), чтобы при решении задачи соответствующие значения переменных оказались заведомо равными нулю. Обозначим через xij факт назначения i-го рабочего на выполнение j-й операции (1 – если рабочий назначен, 0 – если не назначен). Найти такие значения xij, чтобы суммарное время на выполнение всех работ было наименьшим. Целевая функция: 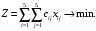  Ограничения имеют вид: а) каждый работник назначается только на одну работу: 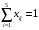 (j=1, 5); (j=1, 5); б) один работник выполняет только одну работу: б) один работник выполняет только одну работу: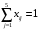 (i=1, 5); (i=1, 5);в) условие не отрицательности: 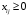 (i=1, 5; j=1,5). (i=1, 5; j=1,5).2. Заполняем таблицу Excel исходными данными (рисунок 1). Блок ячеек D14:H18 содержит оптимальное решение, значение этих ячеек будет получено в результате решения задачи. Блок ячеек D5:H9 содержит значения затрат времени на выполнение операций каждого рабочего для каждой операции. 3. Для вычисления целевой функции в ячейке С24 используем функцию =СУММПРОИЗВ(D5:H9;D14:H18) 4. Вводим ограничения (рисунок 1): по виду работ (каждый работник назначается только на одну работу) в ячейки D19:H19 (=СУММ(D14:D18)) и по выполнению (один работник выполняет только одну работу) в ячейки I14:I18 (=СУММ(D14:H14)).  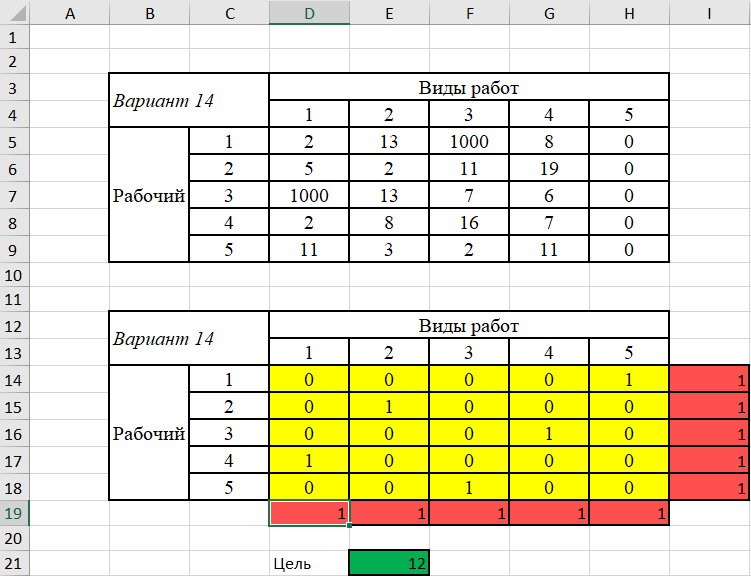 Рисунок 1 5. На вкладке Данные в группе Анализ выберем команду Поиск решения. На экране отобразится ДОПараметры поиска решения, в котором установим следующие параметры (рисунок 2): – в поле Оптимизировать целевую функцию указываем адрес ячейки со значением целевой функции – E21; – переключатель До устанавливаем на минимум целевой функции; – в поле Изменяя ячейки переменных указываем адреса ячеек со значениями искомых переменных D14:H18; – в области В соответствии с ограничениями с помощью кнопки Добавить размещаем все ограничения задачи. 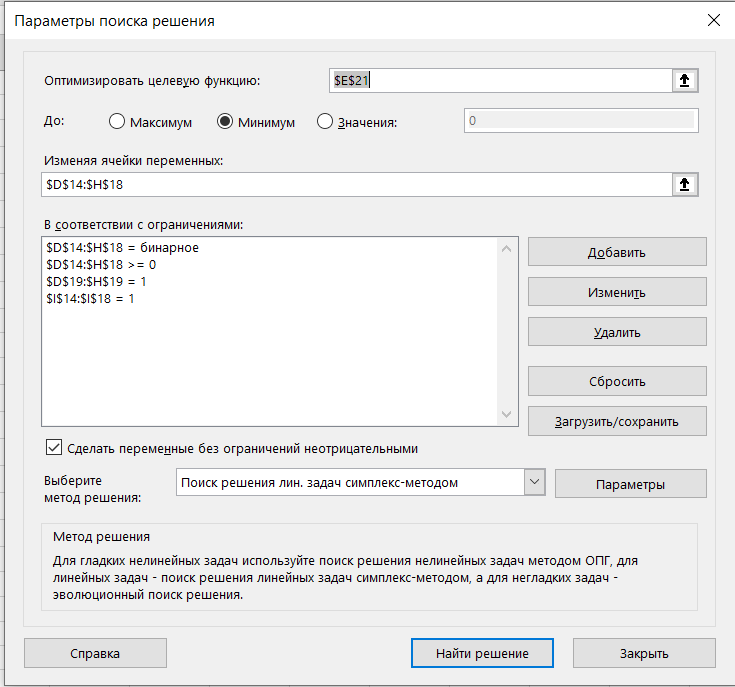 Рисунок 2 Результат выполнения поиска решений представлен на рисунке 3.  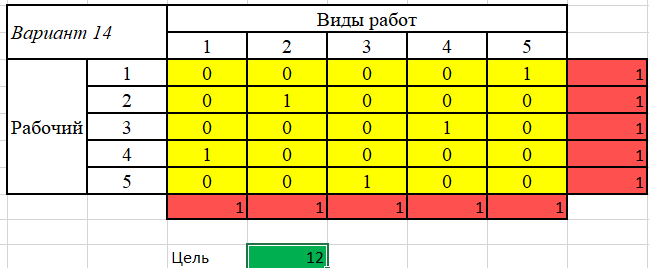 Рисунок 3 Вывод. Минимальное время на выполнение всех операций составит 12 ч при следующих назначениях:  – рабочего 1 на выполнение фиктивного вида работы 5; – рабочего 1 на выполнение фиктивного вида работы 5; – рабочего 2 на выполнение вида работы 2; – рабочего 3 на выполнение вида работы 4; – рабочего 4 на выполнение вида работы 1; – рабочего 5 на выполнение вида работы 3; Рабочего 1, назначенного на выполнение фиктивного вида работы, фактически не работают.  Лабораторная работа №6. Решение задач оптимизации с помощью Excel (закрытая модель транспортной задачи) Лабораторная работа №6. Решение задач оптимизации с помощью Excel (закрытая модель транспортной задачи)Цель работы: получение навыков решения закрытой модели транспортной задачи оптимизации с помощью Excel. Задание: Решить закрытую модель транспортной задачи из таблицы 1. Таблица 1
1. Составляем математическую модель задачи. Целевая функция: 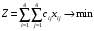 . .Систему ограничений получаем из следующих условий задачи: а) все грузы должны быть перевезены: 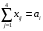 (i=1, 4); (i=1, 4);б) все потребности должны быть удовлетворены: 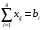 (j=1, 4); (j=1, 4);в) условие не отрицательности: 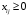 (i=1, 4; j=1, 4). (i=1, 4; j=1, 4).Оптимальным решением задачи будет являться матрица размерностью  4×4, удовлетворяющая системе ограничений и доставляющая минимум целевой функции. 4×4, удовлетворяющая системе ограничений и доставляющая минимум целевой функции.2. Заполняем таблицу Excel исходными данными (рисунок 1). Блок ячеек D12:G15 содержит оптимальное решение, значение этих ячеек будет получено в результате решения задачи. Блок ячеек D5:G8 содержит значения по издержкам перевозок из одного пункта в другой. Блок ячеек H12:H15 содержит значения по имеющимся предложениям (объемам производства). Блок ячеек D16:G16 содержит значения по спросу (объемам поставок). 3. Для вычисления целевой функции в ячейке Е18 используем функцию =СУММПРОИЗВ(D5:G8;D12:G15) (рисунок 1). 4. Вводим ограничения (рисунок 1). – по продавцам (все грузы должны быть перевезены) в ячейку D16 (=СУММ(D12:D15)) и растягиваем формулу до ячейки G16; – по покупателям (все потребности должны быть удовлетворены) в ячейку H12 (=СУММ(D12:G12)) и растягиваем формулу до ячейки H15. 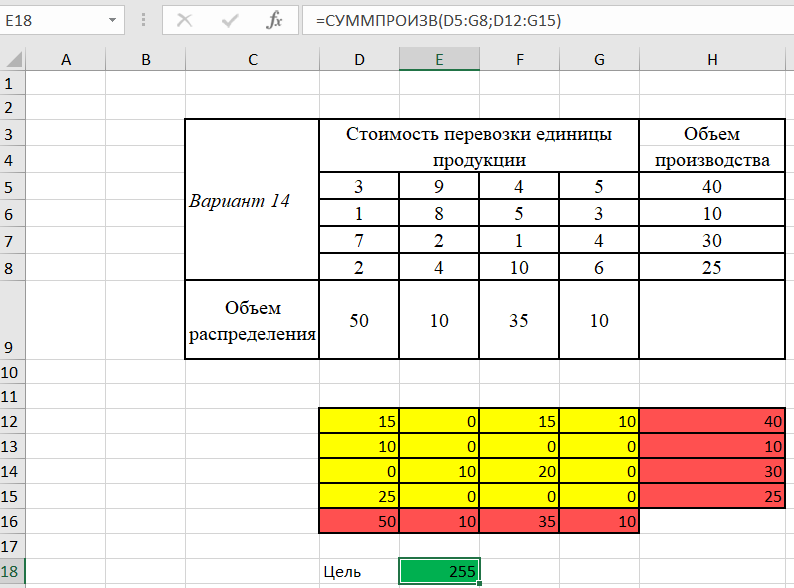 Рисунок 1 5. На вкладке Данные в группе Анализ выберем команду Поиск решения. На экране отобразится ДОПараметры поиска решения, в котором установим следующие параметры (рисунок 2): – в поле Оптимизировать целевую функцию указываем адрес ячейки со значением целевой функции – E18; – переключатель До устанавливаем на минимум целевой функции; – в поле Изменяя ячейки переменных указываем адреса ячеек со значениями искомых переменных D12:G15; – в области В соответствии с ограничениями с помощью кнопки Добавить размещаем ссылки на все ограничения задачи; – проверяем, чтобы обязательно была поставлена галочка напротив опции “Сделать переменные без ограничений неотрицательными”, а также, чтобы в качестве метода решения стояло значение “Поиск решения симплекс методом” и нажимаем кнопку Выполнить. 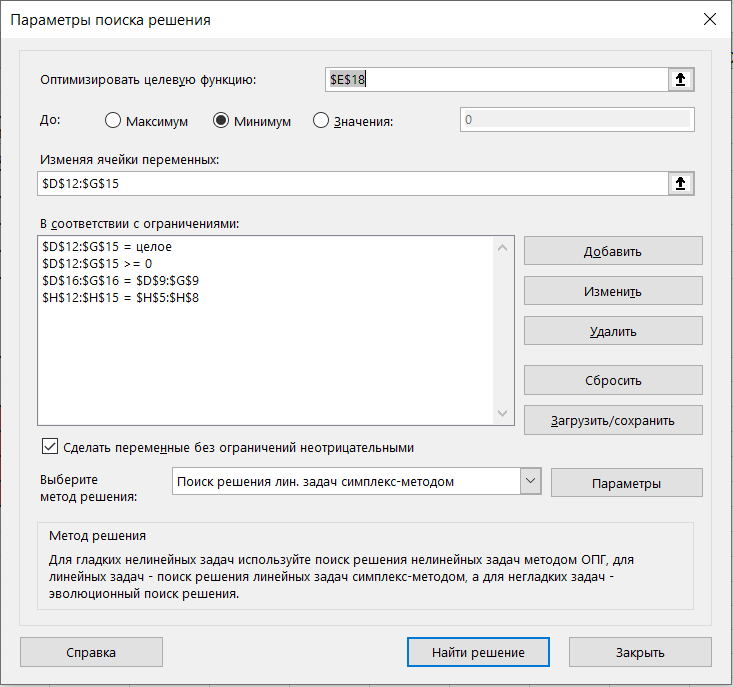 Рисунок 2  Результат выполнения Поиска решений представлен на рисунке 3. Результат выполнения Поиска решений представлен на рисунке 3.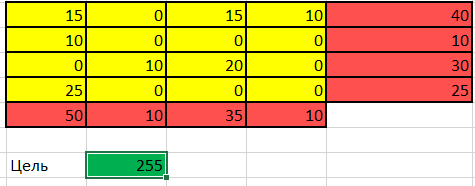  Рисунок 3 Рисунок 3Вывод. Таким образом, для получения минимальных издержек по доставке грузов получен план доставок 4 наименований товаров по 4 покупателям. Лабораторная работа № 7. Решение задач оптимизации с помощью Excel (открытая модель транспортной задачи) Цель работы: получение навыков решения открытой модели транспортной задачи оптимизации с помощью Excel.  Задание: решить закрытую модель транспортной задачи для заданного варианта из таблицы 1. Задание: решить закрытую модель транспортной задачи для заданного варианта из таблицы 1.Таблица 1
Допустим, у нас есть 4 продавца и 4 покупателя. Предложение продавцов составляет 35, 20, 10, и 10 ед. Спрос покупателей следующий: 30, 20, 10, и 10 ед. Суммарные количества по спросу и предложению равны, следовательно, это транспортная задача закрытого типа. Также мы имеем данные по издержкам перевозок из одного пункта в другой Чтобы сбалансировать спрос и предложение, вводим в данном случае еще одного, фиктивного покупателя с потребностью в 5 ед. При этом матрица стоимости перевозок для данного фиктивного пункта назначения заполняется нулями (таблица 2). Таблица 2  1. Составляем математическую модель задачи. Целевая функция (формула (1)) 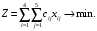 (1) (1)Ограничения получаем из условий задачи (формулы (2) –(4)): а) все грузы должны быть перевезены:  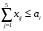 (i=1, 5); (2) (i=1, 5); (2)б) все потребности должны быть удовлетворены: 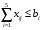 (j=1, 5); (3) (j=1, 5); (3)в) условие не отрицательности: 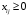 (i=1, 4; j=1, 5). (4) (i=1, 4; j=1, 5). (4)Оптимальным решением задачи является матрица размерностью 4×5,удовлетворяющая системе ограничений и доставляющая минимум целевой функции. 2. Заполняем таблицу Excel исходными данными (рисунок 1). Блок ячеек D13:H16 содержит оптимальное решение, значение этих ячеек будет получено в результате решения задачи. Блок ячеек D5:H8 содержит значения по издержкам перевозок из одного пункта в другой. Блок ячеек I5:I8 содержит значения по имеющимся предложениям (объемам производства). Блок ячеек D9:H9 содержит значения по спросу (объемам поставок). 3. Для вычисления целевой функции в ячейке D19 используем функцию =СУММПРОИЗВ(D5:H8;D13:H16) (рисунок 1). 4. Вводим ограничения (рисунок 1): по продавцам (все грузы должны быть перевезены) в ячейки I13:I16 (=СУММ(D13:H13)) и по покупателям (все потребности должны быть удовлетворены) в ячейки D17:H17 (=СУММ(D13:D16)). 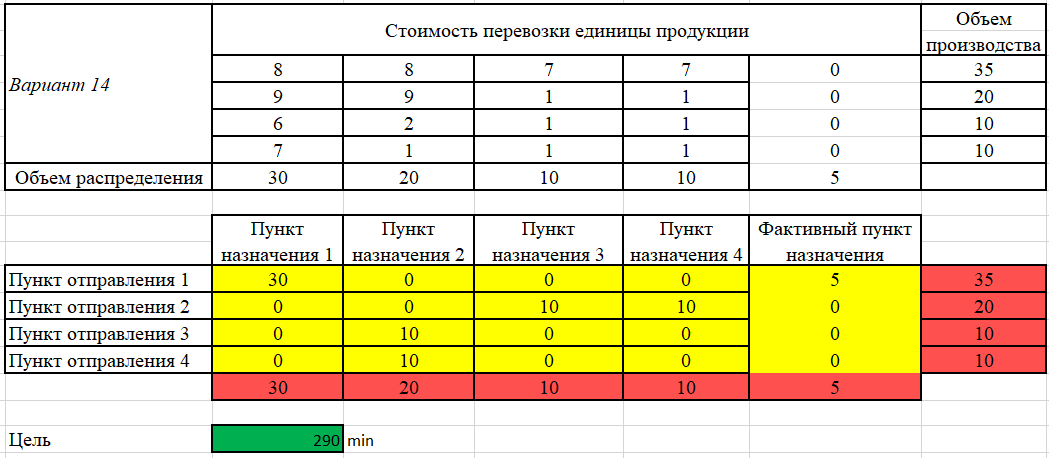  Рисунок 1 Рисунок 15 На вкладке Данные в группе Анализ выберем команду Поискрешения. На экране отобразится ДОПараметрыпоискарешения, в котором установим следующие параметры (рисунок 2): – в поле Оптимизироватьцелевуюфункцию указываем адрес ячейки со значением целевой функции – $D$19; – переключатель До устанавливаем на минимум целевой функции; – в поле Изменяя ячейки переменных указываем адреса ячеек со значения-ми искомых переменных – $D$13:$H$16; – в области В соответствии с ограничениями с помощью кнопки Добавить размещаем все ограничения задачи; – проверяем, чтобы обязательно была поставлена галочка напротив опции Сделать переменные без ограничений неотрицательными, а также чтобы в качестве метода решения стояло значение Поиск решения линейных задач симплекс-методом и нажимаем кнопку Выполнить. 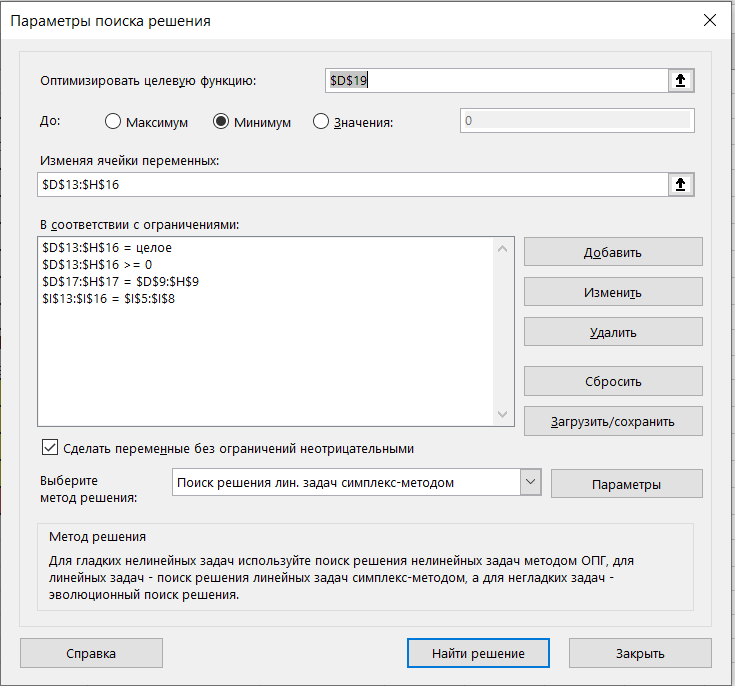 Рисунок 2 Результат выполнения Поиска решений представлен на рисунке 3. 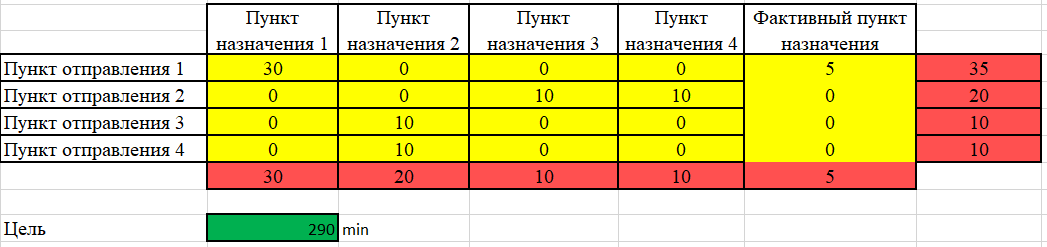 Рисунок 3  Вывод: Таким образом, для получения минимальных издержек по доставке грузов получен план доставок 4 наименований товаров по 4 покупателям, 5 единиц производства оставить на складе в пункте отправления 1. Вывод: Таким образом, для получения минимальных издержек по доставке грузов получен план доставок 4 наименований товаров по 4 покупателям, 5 единиц производства оставить на складе в пункте отправления 1. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
