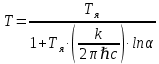Физика лабораторная работа 6. Лабораторная работа 6. 1 Изучение закона стефанабольцмана выполнили студенты группы аб106 Фильберт Роман Андреевич
 Скачать 191.84 Kb. Скачать 191.84 Kb.
|
|
Федеральное агентство связи ФГБОУ ВО «СибГУТИ» Кафедра физики Лабораторная работа 6.1 ИЗУЧЕНИЕ ЗАКОНА СТЕФАНА-БОЛЬЦМАНА Выполнили студенты группы: АБ-106 Фильберт Роман Андреевич Русаков Дмитрий Романович Проверил преподаватель: Черевко А.Г. Измерения сняты Дата, подпись преподавателя Отчет принят Дата, подпись преподавателя Работа зачтена Оценка дата, подпись преподавателя 1. ЦЕЛЬ РАБОТЫ 1. Изучить закон Стефана-Больцмана. 2. Определить постоянную Стефана-Больцмана. 3. Познакомиться с принципом действия оптического пирометра и научиться пользоваться им. 2. ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ Излучением тел называется испускание телами в окружающее пространство электромагнитных волн. Излучение может возникать по разным причинам. Излучение, возникающее за счет внутренней энергии тел, т.е. вследствие теплового движения атомов и молекул, входящих в состав излучающего тела, называется тепловым или температурным. Тепловое излучение имеет место при любых температурах тел Совокупность частот, входящих в состав излучения, называется спектром излучения. Тепловое излучение твердых и жидких тел содержит все частоты от 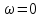 до до 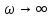 . Поэтому спектр теплового излучения твердых и жидких тел называется сплошным. В данной работе рассматривается излучение твердых тел. . Поэтому спектр теплового излучения твердых и жидких тел называется сплошным. В данной работе рассматривается излучение твердых тел.Для описания теплового излучения используется несколько характеристик. Среди них большое значение имеют понятия излучательной способности 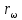 , и энергетической светимости R. , и энергетической светимости R.Излучательной способностью 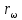 называют количество энергии, которое излучается с единицы площади поверхности тела по всем направлениям за одну секунду в единичном спектральном интервале на частоте называют количество энергии, которое излучается с единицы площади поверхности тела по всем направлениям за одну секунду в единичном спектральном интервале на частоте 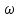 . Если интервал излучаемых частот равен . Если интервал излучаемых частот равен 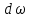 в окрестности частоты в окрестности частоты 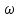 , элемент поверхности, с которого происходит излучение, равен dS, время, в течение которого осуществляется излучение равно dt, и при этих условиях по всем направлениям в окружающее пространство излучается энергия dW, то: , элемент поверхности, с которого происходит излучение, равен dS, время, в течение которого осуществляется излучение равно dt, и при этих условиях по всем направлениям в окружающее пространство излучается энергия dW, то: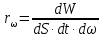 Так как 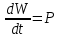 есть мощность, излучаемая, телом, то формулу (1) можно истолковать по-другому. Можно сказать, что излучательной способностью тела называется мощность, излучаемая телом на частоте 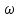 в единичном спектральном интервале с единицы поверхности по всем направлениям: в единичном спектральном интервале с единицы поверхности по всем направлениям: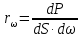 Излучательная способность тел, при заданной температуре заисит от частоты излучения. Эту зависимость называют распределением энергии в спектре излучения тела. Чтобы объяснить наблюдающееся на опыте распределение энергии в спектре излучения черного тела, Макс Планк предположил, что энергия при тепловом излучении порциями, которые он назвал квантами энергии. При этом энергия одного кванта равна 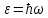 Здесь: 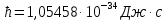 – так называемая постоянная Планка, а – так называемая постоянная Планка, а 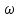 – циклическая частота, на которой осуществляется излучение. – циклическая частота, на которой осуществляется излучение.Благодаря указанной гипотезе, Планку удалось поучить формулу, описывающую распределение энергии в спектре излучения абсолютно черного тела. Эта формула получила название формулы Планка и имеет вид: 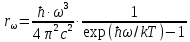 Энергетической светимостью Rназывается количество энергии, излучаемое с единицы площади тела по всем направлениям за одну секунду во всем диапазоне излучаемых частот: 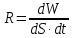 Учитывая (2), можно сказать, что энергетической светимостью называется мощность, излучаемая с единицы поверхности тела по всем направлениям во всем диапазоне излучаемых частот. 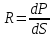 Из определения энергетической светимости вытекает, что: 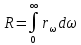 Если подставить (5) в формулу (8) и взять интеграл, то получим: 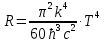 Дробь, стоящая перед T, состоит из одних только констант и потому является константой. Обозначим ее через 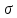 : :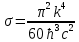 Величину 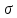 называют постоянной Стефана или постоянной Стефана-Больцмана. Ее вычисление по (10) дает значение называют постоянной Стефана или постоянной Стефана-Больцмана. Ее вычисление по (10) дает значение 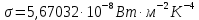 . С учетом (10), получаем: . С учетом (10), получаем: Таким образом, энергетическая светимость абсолютно черного тела пропорциональна четвертой степени абсолютной температуры. Формула (11) получила название закона Стефана-Больцмана. Реальные тела не являются абсолютно черными и, строго говоря, формула (11) к ним неприменима. Однако, во многих случаях энергетическая светимость 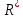 реальных тел с достаточной степенью точности пропорциональна четвертой степени температуры, и, если ввести зависящий от материала нагретого тела поправочный множитель реальных тел с достаточной степенью точности пропорциональна четвертой степени температуры, и, если ввести зависящий от материала нагретого тела поправочный множитель 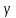 , то можно сказать, что , то можно сказать, что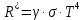 Коэффициент 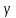 часто называют коэффициентом черноты материала, из которого состоит излучающее тело. Этот коэффициент зависит от материала, температуры, состояния поверхности и других факторов. В нашей работе коэффициент черноты материала принят равным 0.17. Если площадь поверхности пластины S, то излучаемая пластиной мощность P будет: часто называют коэффициентом черноты материала, из которого состоит излучающее тело. Этот коэффициент зависит от материала, температуры, состояния поверхности и других факторов. В нашей работе коэффициент черноты материала принят равным 0.17. Если площадь поверхности пластины S, то излучаемая пластиной мощность P будет: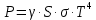 Целью нашей работы является проверка пропорциональности излучаемой мощности четвертой степени температуры и определение постоянной Стефана-Больцмана. Для достижения поставленной цели, воспользуемся следующим методом. Возьмем источник излучений в виде металлической пластины, запаянной в стеклянную колбу, из которой откачан воздух, и имеющей металлические выводы для включения пластины в электрическую цепь. Эта пластина будет рабочим телом. Назовем такое устройство лампой. Включим лампу в электрическую цепь. При прохождении электрического тока, в пластине будет выделяться энергия. Выделяемая электрическая мощность 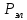 , равна , равна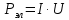 Где I – сила тока в пластине, а U – напряжение на выводах пластины из лампы. Мощность 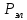 частично теряется на нагревание окружающей среды путем теплопроводности и конвекции, а частично преобразуется в излучение. Отношение излучаемой мощности к мощности, выделяемой в пластине электрическим током, называют излучательным коэффициентом полезного действия (к.п.д.) лампы (пластины). В пределах данной работы мы будем считать, что коэффициентом полезного действия η равен 0.21, поэтому: частично теряется на нагревание окружающей среды путем теплопроводности и конвекции, а частично преобразуется в излучение. Отношение излучаемой мощности к мощности, выделяемой в пластине электрическим током, называют излучательным коэффициентом полезного действия (к.п.д.) лампы (пластины). В пределах данной работы мы будем считать, что коэффициентом полезного действия η равен 0.21, поэтому: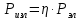 Поскольку лампа находится в среде с температурой 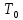 , ее пластина одновременно с излучением поглощает энергию из окружающего пространства в виде излучений. Поглощаемая из окружающего пространства мощность , ее пластина одновременно с излучением поглощает энергию из окружающего пространства в виде излучений. Поглощаемая из окружающего пространства мощность 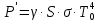 Следовательно, теряемая пластиной засчет излучения мощность 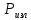 равна равна 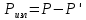 или 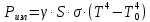 Учитывая (15), можно записать: 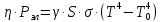 В нашей работе рабочее тело (пластина) имеет температуру Т ≈ 1000К, а температура окружающей среды (комнатная) 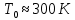 . Отсюда следует, что . Отсюда следует, что 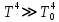 и, пренебрегая вторым слагаемым, (19) можно представить в виде: и, пренебрегая вторым слагаемым, (19) можно представить в виде: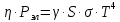 Таким образом, подводимая к лампе электрическая мощность, должна быть пропорциональна четвертой степени температуры пластины в лампе. Чтобы проверить справедливость формулы (20) и, следовательно, закона Стефана-Больцмана, необходимо независимо измерить подводимую к пластине электрическую мощность 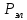 и температуру и температуру 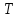 пластины, а затем построить график зависимости пластины, а затем построить график зависимости 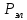 от от 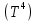 . В случае справедливости закона Стефана-Больцмана эта зависимость должна быть линейной. Теперь, учитывая (15), выразим из (20) . В случае справедливости закона Стефана-Больцмана эта зависимость должна быть линейной. Теперь, учитывая (15), выразим из (20) 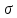 и получим рабочую формулу для вычисления постоянной Стефана-Больцмана: и получим рабочую формулу для вычисления постоянной Стефана-Больцмана: 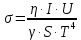 3. ОТВЕТЫ НА КОНТРОЛЬНЫЕ ВОПРОСЫ 1. Какое излучение называется тепловым или температурным? Излучение, возникающее за счет внутренней энергии тел, т.е. вследствие теплового движения атомов и молекул, входящих в состав излучающего тела, называется тепловым или температурным. 2. Что называется энергетической светимостью тела? Энергетической светимостью Rназывается количество энергии, излучаемое с единицы площади тела по всем направлениям за одну секунду во всем диапазоне излучаемых частот: 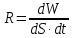 3. Что называется излучательной способностью тела? Поясните физический смысл этого термина и его связь с энергетической светимостью. Излучательной способностью тела называется мощность, излучаемая телом на частоте 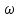 в единичном спектральном интервале с единицы поверхности по всем направлениям: в единичном спектральном интервале с единицы поверхности по всем направлениям: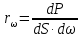 Излучательная способность тел, при заданной температуре заисит от частоты излучения. Эту зависимость называют распределением энергии в спектре излучения тела, то есть нужно использовать формулу Планка. 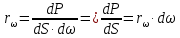 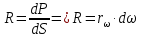 4. Какие тела называют абсолютно черными? Абсолютно чёрное тело — физическое тело, которое при любой температуре поглощает всё падающее на него электромагнитное излучение во всех диапазонах. 5. Дайте пояснения к формуле Планка для распределения энергии в спектре излучения абсолютно черного тела. 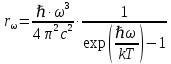 (5) (5)Здесь: 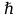 =1,05458*10-34 Дж·с - так называемая постоянная Планка, а - циклическая частота, на которой осуществляется излучение. с-скорость света, T- температура, k- постоянная Больцмана. =1,05458*10-34 Дж·с - так называемая постоянная Планка, а - циклическая частота, на которой осуществляется излучение. с-скорость света, T- температура, k- постоянная Больцмана.6. Сделайте вывод закона Стефана-Больцмана из формулы Планка. Энергетической светимостью R называется количество энергии, излучаемое с единицы площади тела по всем направлениям за одну секунду во всем диапазоне излучаемых частот: 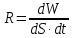 (6) (6)Учитывая (2), можно также сказать, что энергетической светимостью называется мощность, излучаемая с единицы поверхности тела по всем направлениям во всем диапазоне излучаемых частот. 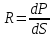 (7) (7)Из определения энергетической светимости вытекает, что: 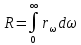 (8) (8) Если подставить (5) в формулу (8) и взять интеграл, то получим: 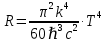 (9) (9)Дробь, стоящая перед Т, состоит из одних только констант и потому является константой. Обозначим ее через : 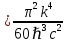 (10) (10)Величину называют постоянной Стефана или постоянной Стефана-Больцмана. Ее вычисление по (10) дает значение 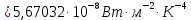 . С учетом (10), получаем: . С учетом (10), получаем: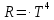 (11) (11)Таким образом, энергетическая светимость абсолютно черного тела пропорциональна четвертой степени абсолютной температуры. Формула (11) получила название закона Стефана-Больцмана. 7. Сформулируйте гипотезу Планка. Излучательная способность тел при заданной температуре зависит от частоты излучения. Эту зависимость называют распределением энергии в спектре излучения тела. Чтобы объяснить наблюдающееся на опыте распределение энергии в спектре излучения черного тела, Макс Планк предположил, что энергия при тепловом излучении испускается и поглощается порциями, которые он назвал квантами энергии. При этом энергия одного кванта равна 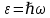 (4) (4)Здесь: 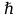 =1,05458*10-34 Дж·с - так называемая постоянная Планка, а - циклическая частота, на которой осуществляется излучение. =1,05458*10-34 Дж·с - так называемая постоянная Планка, а - циклическая частота, на которой осуществляется излучение.8. Сделайте вывод расчетной формулы для определения постоянной Стефана-Больцмана. 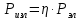 (15) (15)Поскольку лампа находится в среде с температурой T0, её пластина одновременно с излучением поглощает энергию из окружающего пространства в виде излучений. Поглощаемая из окружающего пространства мощность P , в соответствии с (13) равна: 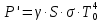 (16) (16)Следовательно, теряемая пластиной за счет излучения мощность Pизл равна 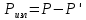 (17) (17)или 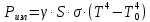 (18) (18)Учитывая (15), можно записать: 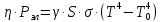 (19) (19)В нашей работе рабочее тело (пластина) имеет температуру T 1000 K , а температура окружающей среды (комнатная) T0 300 K . Отсюда следует, что T4 >> T04 и, пренебрегая вторым слагаемым, (19) можно представить в виде: 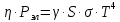 (20) (20)Теперь, учитывая (15), выразим из (20) и получим рабочую формулу для вычисления постоянной Стефана-Больцмана: 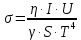 (21) (21)9. Поясните принцип действия оптического пирометра и порядок работы с ним. Измерение температуры с помощью пирометра основано на сравнении яркостей светящегося рабочего тела и нити измерительной лампы пирометра. В соответствии с формулой Планка (8), излучение нагретого рабочего тела в каком-либо спектральном интервале, в нашем случае на длине волны 660 нм, зависит от температуры рабочего тела. С увеличением температуры тела растет и его излучательная способность. В пирометре при помощи реостата (10) (рис.1.2 и 1.3) регулируется ток в цепи нити накала лампы так, чтобы яркость свечения нити (4) накала измерительной лампы сравнялась с яркостью изображения светящегося тела. При этом изображение нити исчезает на фоне изображения светящегося тела. Поэтому данный пирометр часто называют пирометром с исчезающей нитью. При равных яркостях светящегося тела (1) и нити (4) пирометра, их температуры связаны однозначной зависимостью. Поэтому шкалу вольтметра (9), рис.1.2 и 1.3, можно проградуировать в единицах температуры светящегося тела. Такая градуировка производится при изготовлении пирометра по излучению черного тела на длине волны 660 нм. Пирометры, используемые в наших лабораторных установках, проградуированы в шкале Цельсия. Следовательно, полученные при измерениях значения температур необходимо преобразовать в шкалу Кельвина. 10. Поясните, в чем состоит проверка правильности закона Стефана-Больцмана. Чтобы проверить справедливость формулы (20) и, следовательно, закона Стефана-Больцмана, необходимо независимо измерить подводимую к пластине электрическую мощность Pэл и температуру T пластины, а затем построить график зависимости Pэл от (T4). В случае справедливости закона Стефана-Больцмана эта зависимость должна быть линейной ЗАДАЧИ К ЛАБОРАТОРНОЙ РАБОТЕ 1.1 Раскаленная металлическая поверхность площадью 10 см2 излучает в 1 мин 105 Дж. Температура поверхности 2500 К. Найдите: 1) Излучение этой поверхности, если бы она была абсолютно черной. 2) Отношение энергетической светимости этой поверхности и абсолютно черного тела при данной температуре. Дано: S = 10см2 = 10-3м2 ΔW = 105 Дж Δt = 1 мин = 60 с Т = 2500 К Найти: 1. Rповачт - ? 2. Rпов / Rачт - ?
1.2. При нагревании абсолютно черного тела длина волны, на которую приходится максимум спектральной плотности энергетической светимости, изменилась от 690 нм до 500 нм. Во сколько раз увеличилась при этом энергетическая светимость тела? Дано: λ1 = 690 *10-9 м λ2 = 500 *10-9 м Найти: R1 / R2 - ?
1.3. Какую мощность надо подводить к зачерненному шарику радиусом 1 см, чтобы поддерживать его температуру на 27 градусов выше температуры окружающей среды? Температура окружающей среды равна 20оС. Дано: r = 1 см = 0,01 м Δt = 27 оС = 300 K tокр = 20 оС = 293 Найти: P - ?
1.4. Найдите, насколько уменьшится масса Солнца за год вследствие излучения. Температуру поверхности Солнца принять равной 5800 К и считать Солнце абсолютно черным телом Дано: Т = 5800 К Rc = 696000000 м t = 31 536 000 с Найти: Δm - ?
Дано: λ = 400 *10-9 м Найти: 1. Т - ? 2. R - ? 4. ОПИСАНИЕ УСТАНОВКИ Схема установки показана на рис.1.1. Установка состоит из тумблера (1), регулируемого трансформатора (2), амперметра (3), вольтметра (4), источника электромагнитных излучений (лампы) (5) и оптического пирометра (6). Рабочим телом является вольфрамовая пластина, установленная в лампе (5). 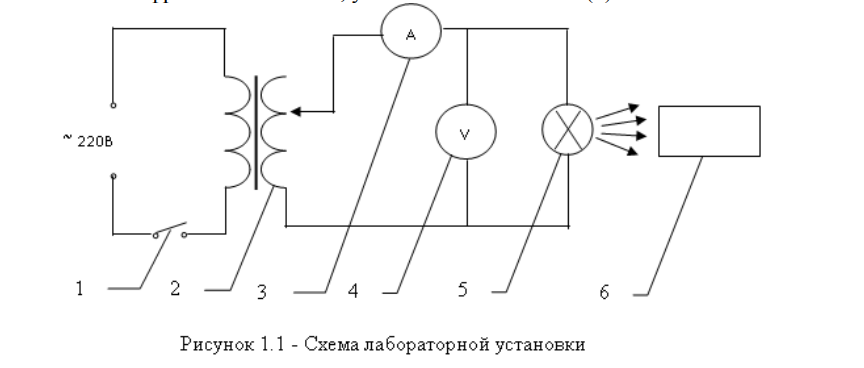 При помощи трансформатора подводится электрическая энергия к рабочему При помощи трансформатора подводится электрическая энергия к рабочемутелу. Амперметр позволяет измерять силу тока лампы, а вольтметром измеряется 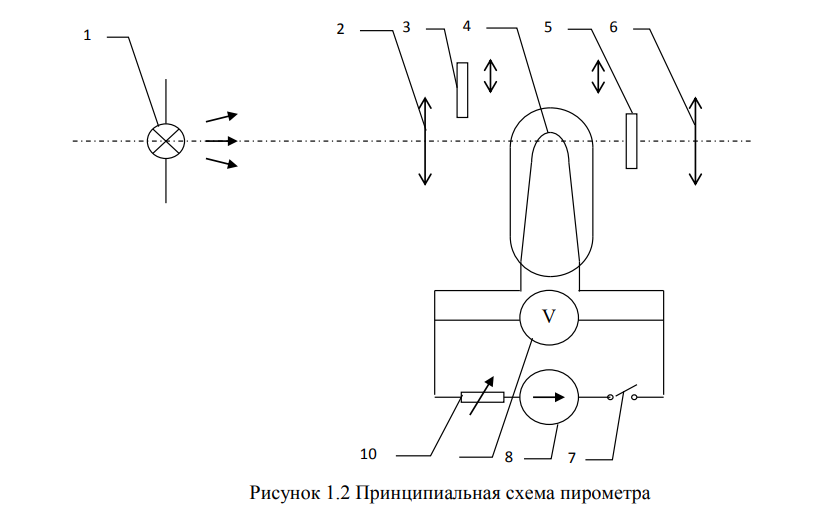 напряжение на зажимах лампы (рабочего тела). Пирометр предназначен для дистанционного измерения температуры рабочего тела. Принципиальная схема пирометра приведена на рис.1.2. Внешний вид пирометра представлена на рис 1.3. 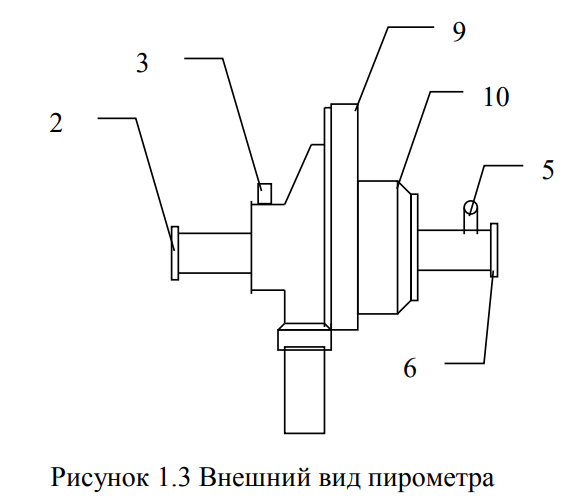 Здесь: 1 – рабочее тело; 2 – объектив пирометра; 3 – нейтральный ослабляющий светофильтр; 4 – измерительная лампа накаливания с нитью; 5 – красный светофильтр; 6 – окуляр пирометра; 7 – ключ для запитывания электрической цепи пирометра; 8 – источник питания пирометра; 9 – вольтметр, шкала которого проградуирована в единицах температуры по шкале Цельсия; 10 – реостат, для регулировки тока в цепи нити накала лампы. Электромагнитные волны, излучаемые нагретым рабочим телом (1), (рис.1.2) попадают в объектив (2) пирометра. В фокусе объектива находится измерительная лампа накаливания с нитью (4), изогнутой в форме дуги. Окуляр (6) позволяет одновременно видеть нить измерительной лампы и изображение накаленного тела, через красный светофильтр (5). Светофильтр вырезает участок спектра излучения в окрестности длины волны 660 нм. Измерение температуры с помощью пирометра основано на сравнении яркостей светящегося рабочего тела и нити измерительной лампы пирометра. В соответствии с формулой Планка (8), излучение нагретого рабочего тела в каком-либо спектральном интервале, в нашем случае на длине волны 660 нм, зависит от температуры рабочего тела. С увеличением температуры тела растет и его излучательная способность. В пирометре при помощи реостата (10) (рис.1.2 и 1.3) регулируется ток в цепи нити накала лампы так, чтобы яркость свечения нити (4) накала измерительной лампы сравнялась с яркостью изображения светящегося тела. При этом изображение нити исчезает на фоне изображения светящегося тела. Поэтому данный пирометр часто называют пирометром с исчезающей нитью. При равных яркостях светящегося тела (1) и нити (4) пирометра, их температуры связаны однозначной зависимостью. Поэтому шкалу вольтметра (9), рис.1.2 и 1.3, можно проградуировать в единицах температуры светящегося тела. Такая градуировка производится при изготовлении пирометра по излучению черного тела на длине волны 660 нм. Пирометры, используемые в наших лабораторных установках, проградуированы в шкале Цельсия. Следовательно, полученные при измерениях значения температур необходимо преобразовать в шкалу Кельвина. Температура, измеренная при помощи пирометра с исчезающей нитью, называется яркостной температурой ( 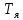 ). Для абсолютно черных тел яркостная температура является истинной температурой тела. Излучение обычных тел отличается от излучения абсолютно черного тела, поэтому для обычных тел яркостная температура отличается от реальной температуры Т тела. Для получения истинной температуры рабочего тела необходимо ввести поправку по формуле: ). Для абсолютно черных тел яркостная температура является истинной температурой тела. Излучение обычных тел отличается от излучения абсолютно черного тела, поэтому для обычных тел яркостная температура отличается от реальной температуры Т тела. Для получения истинной температуры рабочего тела необходимо ввести поправку по формуле: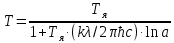 где 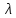 = 660 нм – длина волны, на которой выполняется измерение; k – постоянная Больцмана; = 660 нм – длина волны, на которой выполняется измерение; k – постоянная Больцмана; 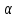 = 0,46 – коэффициент, зависящий от материала нагретого тела; = 0,46 – коэффициент, зависящий от материала нагретого тела; 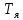 – яркостная температура по шкале Кельвина, которая связана с температурой – яркостная температура по шкале Кельвина, которая связана с температурой 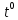 , измеренной по шкале Цельсия соотношением , измеренной по шкале Цельсия соотношением 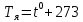 , К; измеренной по шкале Цельсия соотношением , К; измеренной по шкале Цельсия соотношением 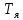 = 𝑡 = 𝑡0 + 273, К; ℏ – постоянная Планка (редуцированная); с – скорость света в вакууме. Оптический пирометр имеет два предела измерений. При использовании шкалы высоких температур перед нитью вводится нейтральный ослабляющий светофильтр (3), рис.1.2 и 1.3. Таблица 1
Измерения t0, C (в таблицу внесено среднее значение данных измерений, чтобы снизить погрешность, (t0, C, где n от 1 до 10): 1) 1018, 1017, 1018, 1018, 1019, 1018, 1018, 1018, 1018, 1018 2) 1040, 1040, 1042, 1041, 1042, 1042, 1041, 1041, 1040, 1041 3) 1059, 1059, 1059, 1058, 1059, 1060, 1059, 1059, 1060, 1059 4) 1098, 1098, 1100, 1098, 1098, 1098, 1099, 1098, 1098, 1098 5) 1140, 1140, 1140, 1141, 1141, 1142, 1141, 1141, 1141, 1141 6) 1180, 1183, 1182, 1181, 1183, 1183, 1183, 1182, 1183, 1183 7) 1251, 1252, 1252, 1251, 1253, 1254, 1252, 1252, 1252, 1252 8) 1284, 1284, 1283, 1284, 1284, 1283, 1284, 1284, 1283, 1284 9) 1359, 1359, 1359, 1359, 1359, 1360, 1359, 1359, 1360, 1360 10) 1400, 1400, 1401, 1402, 1402, 1402, 1402, 1402, 1402, 1402 Используемые формулы:
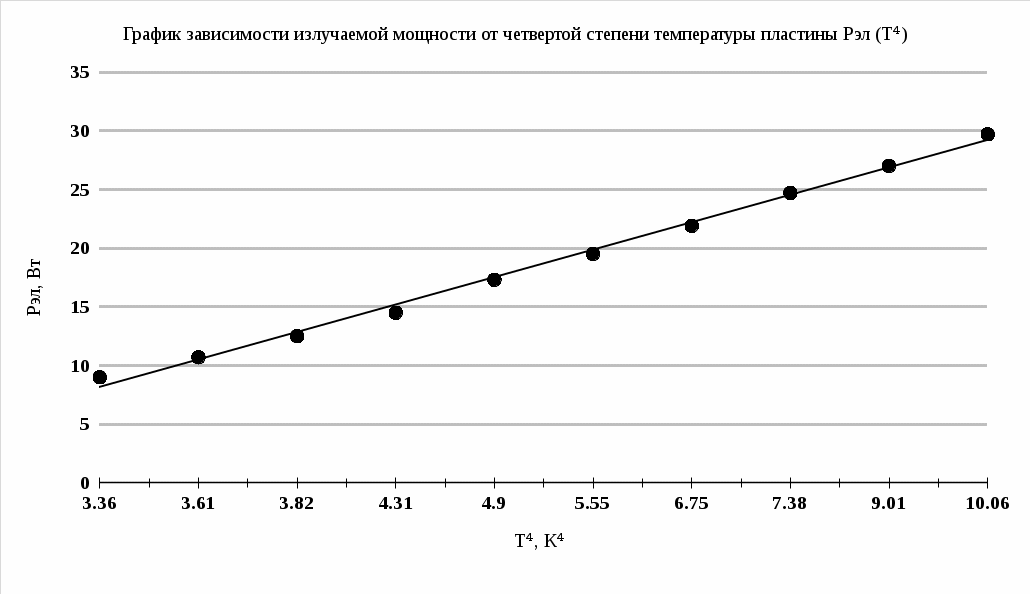 Таблица 2
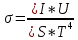 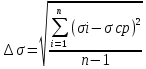 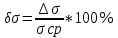 σ = 6,56 ±0,56 δσср = 8,53 n = 10 Вывод: в ходе работы был выведен закон Стефана-Больцмана с помощью формулы Планка, а также постоянная Стефана-Больцмана: 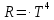 При построении зависимости и апроксимации излучаемой мощности от четвертой степени температуры пластины Pэл (T⁴) была выявлена линейная зависимость вышеупомянутой функции. |

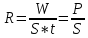
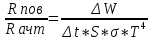
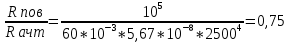
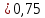
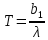
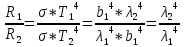
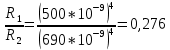
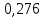
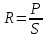

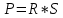
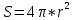
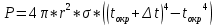
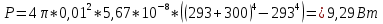
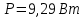
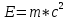
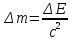
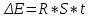
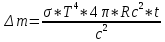
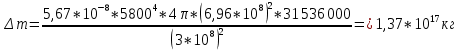
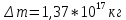
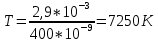
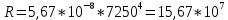
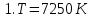 ,
,