Контрольная работа. Лабораторная работа 6,1. Лабораторная работа 6. 1 Поверхностные явления
 Скачать 0.51 Mb.
|
|
Лабораторная работа №6.1 ПОВЕРХНОСТНЫЕ ЯВЛЕНИЯ Цель работы. Определение поверхностного натяжения растворов, изучение зависимости поверхностного натяжения от концентрации раствора, вычисление величины адсорбции и построение изотермы адсорбции. Оборудование. Прибор для определения поверхностного натяжения растворов (рис.1). Мерная колба емкостью 50 мл. Пипетка. Бюретка. Стакан емкостью 200 мл. Колбы, 8 шт. Реактивы. Дистиллированная вода. Изобутиловый спирт. Суть работы. Для измерения поверхностного натяжения существует большое число экспериментальных методов. В данной работе используется метод Ребиндера – метод наибольшего давления пузырьков. Сущность этого метода заключается в определении давления, которое необходимо для отрыва пузырька воздуха от капилляра, погруженного в жидкость. Это давление пропорционально поверхностному натяжению: 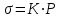 (1)Коэффициент пропорциональности К является постоянной прибора и определяется по стандартной жидкости с известным поверхностным натяжением. Определение поверхностного натяжения методом наибольшего давления пузырьков производится с помощью прибора, изображенного на рис.1. Рат  Рис.1. Схема установки: 1 – трубка с капиллярным кончиком; 2 – пробирка с исследуемой жидкостью; 3 – манометр; 4 – аспиратор; 5 – кран; 6 – исследуемая жидкость. С помощью аспиратора в пробирке над жидкостью создается разрежение. Под действием атмосферного давления (Рат) на конце капилляра постепенно формируется пузырек воздуха, и, при каком-то критическом разрежении в системе, пузырек проскакивает через жидкость. При этом давление газа в пузырьке определяется первым законом Лапласа 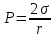 ,где r – радиус капилляра. Максимальное давление газа в пузырьке достигается при максимальном значении его радиуса, который соответствует радиусу капилляра. В растворах изменение σ происходит при адсорбции так называемых поверхностно-активных веществ. Это обычно органические соединения, молекулы которых состоят из углеводородной цепочки и функциональной группы (-СООН, -ОН, -СОН и др.). Такие молекулы имеют сродство к полярной и неполярной фазам и на границе раздела фаз соответственно ориентируются. Поскольку поверхностно-активные вещества понижают поверхностное натяжение, они выталкиваются из раствора на поверхность – адсорбируются на поверхности. Следовательно, способность вещества понижать поверхностное натяжение является причиной адсорбции. Между концентрацией адсорбированного вещества в поверхностном слое Г и концентрацией его в растворе С существует зависимость, которая описывается уравнением адсорбции Гиббса: 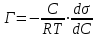 ,где 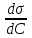 - поверхностная активность. Для ее нахождения используют изотерму σ = f(С) (рис.2.)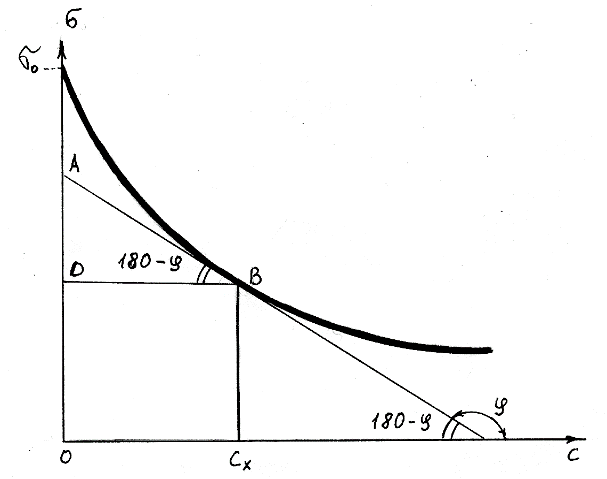 Рис.2. Зависимость поверхностного натяжения от концентрации раствора. σ0 – поверхностное натяжение чистого растворителя. Графически 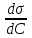представляет собой тангенс угла наклона касательной, проведенной в точке В, соответствующей данной концентрации Сх.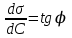 (3)Перейдя к смежному острому углу СхFB, затем параллельному ABD, легко видеть, что ABD=180o-φ. Рассмотрим треугольник ABD. 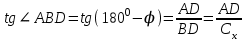 (4) С другой стороны, 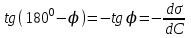 (5) Сравнивая уравнения (4) и (5), получим, что  (6)Подставим найденное выражение (6) для поверхностной активности в уравнение (2), получим 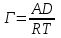 , (7)где R – универсальная газовая постоянная, равная 8,315 Дж/моль град; Т – температура, К. Таким образом, из уравнения (7) следует, что для расчета адсорбции необходимо графически найти величину отрезка AD. Рассчитав Г, легко построить изотерму адсорбции Г=f(с) (рис.3).  Г  СРис.3. Изотерма адсорбции Гиббса Изотерма адсорбции Гиббса проходит через максимум, соответствующий полному насыщению поверхности. Это объясняется тем, что адсорбцией Гиббс называет избыточную концентрацию в поверхности по отношению к раствору, т.е. разность СS- CP где СS – концентрация вещества на поверхности; СР – концентрация этого вещества в глубине раствора. Поэтому, когда достигается насыщение поверхностного слоя и CS становится постоянной, разность (СS- CP) при дальнейшем увеличении концентрации раствора начинает падать. При адсорбции на твердой поверхности (уравнение Фрейндлиха, уравнение Ленгмюра) под адсорбцией подразумевают всю концентрацию вещества на поверхности, т.е. CS. Поэтому при достижении насыщения поверхностного слоя адсорбция становится постоянной. Выполнение работы. Основной частью используемого прибора (рис.1) является капилляр 1, конец которого касается поверхности исследуемой жидкости (рис.4), находящейся в сосуде 2. В этом сосуде создается разрежение за счет вытекания воды из аспиратора 4. Скорость вытекания воды регулируется краном 5. При определенном разрежении через жидкость из капилляра проскакивает пузырек воздуха. Скорость проскакивания пузырьков необходимо регулировать так, чтобы время образования пузырьков составило 10–20 с. При такой скорости образования пузырька в жидкости на поверхности пузырька успевает установиться адсорбционное равновесие. Давление воздуха в капилляре измеряют с помощью манометра 3. Давление фиксируют в момент отрыва пузырька. Измерения повторяют 4-5 раз с точностью до одного мм. Перед началом опыта необходимо аспиратор 4 заполнить водой. Определить постоянную прибора К. Налить в пробирку 2 дистиллированной воды и опустить в воду капилляр так, чтобы погружение его было минимальным (рис.4).  Рис.4 Наполнить аспиратор водой, а затем, постепенно открывая кран 5 (рис.1), отрегулировать равномерный проскок пузырьков. Замерить максимальный перепад уровней (h0) в манометре при проскоке пузырька (рис.1). Результат записать. h0= 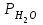 Приготовить 8 растворов изобутилового спирта указанных преподавателем концентраций. Концентрация исходного раствора 1н, объем приготавливаемого раствора 50мл. Для расчета необходимого объема исходного спирта пользуются формулой: С0V0=СV где С0V0 – нормальность и объем исходного 1н раствора спирта; СV – нормальность и объем приготавливаемого раствора спирта. Определить максимальный перепад уровней (h) в манометре при проскоке пузырька через приготовленные растворы, начиная измерения с раствора меньшей концентрации и переходя к растворам с большей концентрацией. Очень важно при переходе от одного раствора к следующему вначале ополаскивать пробирку исследуемым раствором, а затем наливать свежую порцию для определения h. Не менее важно следить, чтобы раствор не попал в отросток пробирки и соединительную резину. Для проведения опыта необходимый объем приготовленного раствора перенести из колбы в сосуд 2 и измерить по манометру максимальное давление Р, при котором отрывается пузырек. Давление Р будет равно h – максимальному перепаду уровней: h=Рспирта. Полученные данные записать в табл.2. 2. По формуле =КР рассчитать поверхностное натяжение каждого из восьми приготовленных растворов спирта. Полученные данные записать в табл.2. Таблица 2
 |