|
|
лабораторная работа №6. Лабораторная работа 6 электромагнитные колебания в параллельном lcконтуре
Министерство образования и науки РФ
Федеральное государственное бюджетное образовательное
учреждение высшего профессионального образования
«Ульяновский государственный университет»
Факультет математики, информационных и авиационных технологий
Отчёт
по дисциплине: «Физика»
Лабораторная работа №6
ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ В ПАРАЛЛЕЛЬНОМ LC-КОНТУРЕ
Выполнили: студенты группы ИТСС-О-20/1 Боровик Д.Д Карташов Д.С
Кулаков И.C
_______ «___» _______ 2020 г.
(подпись) (дата)
Проверил: руководитель работы, старший преподаватель Богданова Д.А.
_______ «___» _______ 2020 г.
(подпись) (дата)
Ульяновск, 2020 г.
Цель работы: исследование параллельного LC-контура в режиме вынужденных колебаний; измерение и вычисление резонансной частоты, полосы пропускания, добротности.
Оборудование: лабораторная установка, генератор сигналов синусоидальной и прямоугольной формы, осциллограф, соединительные провода.
Краткая теория.
Простейшим типом колебаний являются гармонические колебания – колебания, при которых колеблющаяся величина изменяется со временем по закону синуса или косинуса. Гармонические колебания величины s описываются выражениями вида
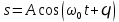 (1) (1)
Время, за которое фаза колебания получает приращение 2π, называется периодом колебания. 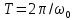 (2) (2)
Величина, равная числу полных колебаний в единицу времени, называется частотой. Пусть ν– частота. Тогда из определения она связана с периодом следующим образом: 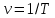 (3) (3)
Сравнивая (2) и (3),получаем: 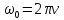 (4) (4)
Коэффициент затухания 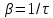 (6) (6)
При рассмотрении вынужденных колебаний также часто применяет-ся величина добротности. В данном случае добротность характеризует остроту резонансных кривых. Рассмотрим ширину кривой (рис.6.4), взятую на высоте 0,7. Величину Δν называют полосой пропускания контура. Относительная ширина полосы пропускания контура оказывается обратно пропорциональной величине его добротности:
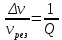 (14) (14)
Экспериментальная установка
Электрическая схема экспериментальной установки представлена на рис.6.5. Для наблюдения резонанса схема подключается к гармоническому выходу генератора, отмеченному символом "". Для наблюдения затухающих колебаний или переходных процессов схема подключается к импульсному выходу генератора/ Для определения параметров контура к нему подключают осциллограф или вольтметр. При резонансе напряжение на контуре максимально, т.к. сопротивление контура в этом случае наибольшее.RCLОсциллограф или вольтметр Генератор НЧРис. 6.5.Электрическая схема для наблюдения резонанса в параллельном LC-контуре Проведение эксперимента1. С гармонического выхода генератора колебаний подать на колебательный контур напряжение около 1В и, изменяя частоту, следить за изменением амплитуды колебаний на контуре с помощью осциллографа или вольтметра. При обнаружении резонансной частоты установить такие пре-делы измерения вольтметра или осциллографа, чтобы было задействовано 0,8–0,9 от максимального значения на этом диапазоне. Установив с помощью изменения частоты генератора в области низких частот амплитуду колебаний на уровне 0,1–0,2 от максимального значения, снять резонансную кривую колебательного контура (U=f(ν)), постепенно увеличивая частоту генератора (с шагом не более 100 Гц). Значения частот определять по шкале генератора.2. Для исследования затухающих колебаний или переходных процессов необходимо с импульсного выхода генератора колебаний подать на колебательный контур напряжение около 1В и наблюдать картину на осциллографе. Частота сигнала должна быть примерно в 10 раз меньше резонансной частоты контура. Воспользовавшись масштабной сеткой на экране осциллографа, определить период затухающих колебаний T. Снять зависимость амплитуды затухающих колебаний от времени UCm=f(t).
Обработка результатов
1. Построить резонансную кривую U/Uрез=f(ν) (Uрез–амплитудное значение напряжения при ν=νрез) и определить по ней полосу пропускания Δν и резонансную частоту νрез. По формуле (14) вычислить добротность контура Q.
2. Воспользовавшись зависимостью UCm=f(t) для затухающих колебаний, определить период T и постоянную времени затухания τ. Вычислить коэффициент затухания β.
3.Рассчитать добротность Q по формуле (11) Q=πτ/T.
4. Сравнить значения добротностей, вычисленных в п.1 и п.3
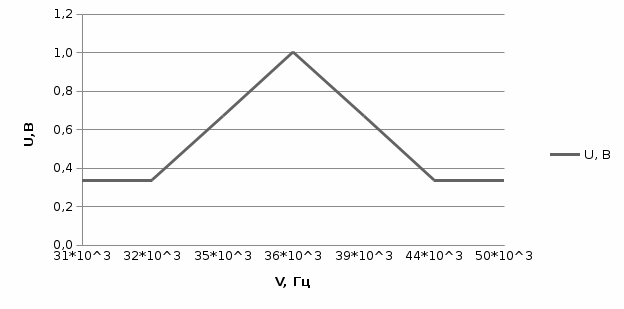
V, Гц
|
31*10^3
|
32*10^3
|
35*10^3
|
36*10^3
|
39*10^3
|
44*10^3
|
50*10^3
|
U, В
|
0,33
|
0,33
|
0,67
|
1,00
|
0,67
|
0,33
|
0,33
|
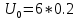 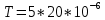
Q=13.3
N=19 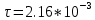
β=1/τ=462.9
Q=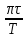 =67.9 =67.9
Вывод: Построив резонансную кривую U/Uрез=f(ν) мы определили по ней добротность контура с помощью формулы (14). Воспользовавшись зависимостью UCm=f(t) для затухающих колебаний мы определили период T и постоянную времени затухания τ, и рассчитали добротность Q по формуле (11) Q=πτ/T. Сравнив значения добротностей, вычисленных в п.1 и п.3 можно сказать |
|
|
 Скачать 30.24 Kb.
Скачать 30.24 Kb.
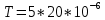
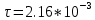
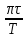 =67.9
=67.9
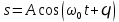 (1)
(1)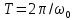 (2)
(2)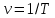 (3)
(3)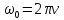 (4)
(4)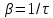 (6)
(6)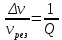 (14)
(14)