теория телетрафика. Работа-6. Лабораторная работа 6 Исследование свойств преобразования Фурье Методические указания и задания
 Скачать 1.58 Mb. Скачать 1.58 Mb.
|
 Федеральное агентство связи Ордена Трудового Красного Знамени федерального государственного бюджетного образовательного учреждения высшего образования «Московский технический университет связи и информатики» Волго-Вятский филиал Кафедра инфокоммуникационных и общепрофессиональных дисциплин (ИКиОПД) Общая теория связи Лабораторная работа № 6 «Исследование свойств преобразования Фурье» Методические указания и задания Выполнил: Проверил: Чернявский А.Д. Нижний Новгород 2021 Цель работы – получение экспериментального подтверждения основных свойств преобразования Фурье. Теоретическая часть Напомним десять основных математических свойств преобразования Фурье, не останавливаясь на их доказательствах: Главное математическое свойство преобразования Фурье состоит в том, что оно однозначно, т. е. каждому сигналу s(t) соответствует только ему присущая спектральная функция S(f), по которой можно однозначно восстановить этот сигнал. Отсюда следует, что преобразование Фурье, примененное к одному и тому же сигналу дважды (сначала к самому сигналу, а затем к его спектральной функции), дает в результате исходный сигнал. Следовательно, если прямое преобразование Фурье сигнала s(t) определено посредством формулы  то сигнал s(t) может быть представлен с помощью интеграла Фурье (или обратного преобразования Фурье)  где S(f) df представляет собой «вклад» от комплексной экспоненты 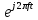 , ,«содержащийся» в s(t) (вследствие этого S(f) также называют спектральной плотностью для s(t)). Или, другими словами, можно сказать, что выражение (4.1) анализирует сигнал s(t) на основе использования ее спектральных составляющих, а (4.2) восстанавливает или синтезирует s(t) из этих составляющих. Теорема Фурье утверждает, что этот процесс анализа-синтеза может выполняться без каких-либо потерь – восстановленный сигнал, согласно теореме, по своей форме идентичен исходному сигналу. Примечание– Теорема Фурье реализована в математических специальных программах, в частности в Mathcad, позволяющих выполнять преобразование Фурье на основе численных методов. С помощью принятой символики математически указанное свойство преобразования Фурье может быть записано следующим образом: Важнейшее свойство преобразования Фурье – это его линейность или аддитивность. Преобразование Фурье от суммы двух сигналов равно сумме преобразований Фурье от каждого из них в отдельности, или Таким образом, когда складываются сигналы, то суммируются и их спектральной функции (частотные спектры). Это свойство легко обобщается на любое число слагаемых. Свойство задержки сигнала во времени. Данное свойство математи-чески записывается следующим образом. Если выполняется равенство то справедливо соотношение Результат (4.7) показывает, что спектральная функция сигнала задержанного во времени на τ отличается от спектральной функции исходного сигнала множителем в виде комплексной экспоненты 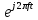 . .Таким образом, амплитудный спектр сигнала задержанного во времени на τ не меняется (ведь модуль такой комплексной экспоненты равен 1), а фазовый спектр приобретает дополнительное слагаемое 2f , линейно зависящее от частоты. Свойство изменения масштаба оси времени. Если выполняется равенство 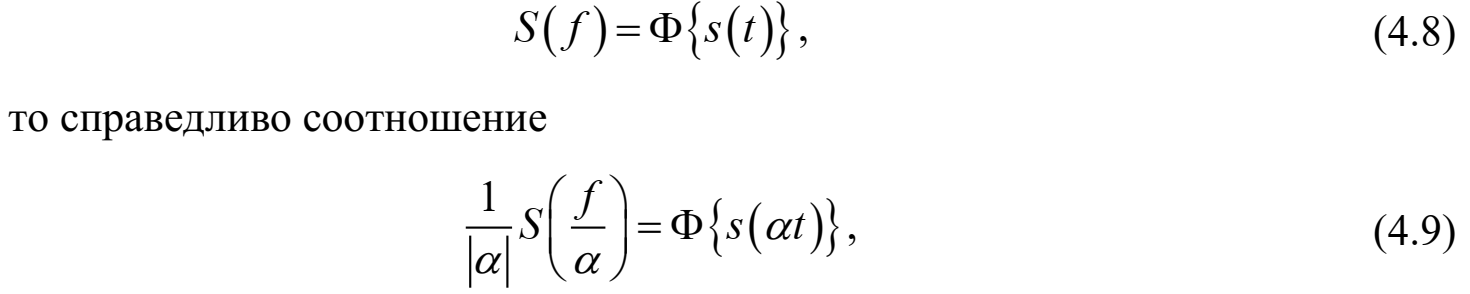 где α – коэффициент изменения масштаба оси времени. Отметим, что при 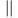 1 сигнал сжимается, при 1 сигнал сжимается, при 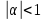 – растягивается. – растягивается.Если 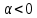 , дополнительно происходит зеркальное отражение сигнала относительно вертикальной оси. Итак, изменение длительности сигнала приводит к изменению ширины его спектра в противоположную сторону (аргумент t на α умножается, а f делится) в сочетании с увеличением (при растяжении, , дополнительно происходит зеркальное отражение сигнала относительно вертикальной оси. Итак, изменение длительности сигнала приводит к изменению ширины его спектра в противоположную сторону (аргумент t на α умножается, а f делится) в сочетании с увеличением (при растяжении, 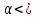 1) или уменьшением (при сжатии, 1) или уменьшением (при сжатии, 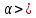 1) уровня спектральных составляющих. В частном случае при 1) уровня спектральных составляющих. В частном случае при 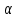 = -1 формула (4.9) дает следующий результат: = -1 формула (4.9) дает следующий результат:Из (4.10) следует, что зеркальное отражение сигнала s(t) относительно начала отсчета времени приводит к зеркальному отражению его спектра относительно нулевой частоты. Для вещественного сигнала это соответствует комплексному сопряжению спектра. Свойство дифференцирование сигнала во временной области. Если выполняется равенство то справедливо соотношение  Спектр производной от сигнала по времени получается путем умножения спектра исходного сигнала на 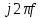 . Таким образом, при дифференцировании низкие частоты спектра сигнала ослабляются, а высокие усиливаются. Фазовый спектр сигнала сдвигается на 90° для положительных частот и на –90° для отрицательных. Множитель . Таким образом, при дифференцировании низкие частоты спектра сигнала ослабляются, а высокие усиливаются. Фазовый спектр сигнала сдвигается на 90° для положительных частот и на –90° для отрицательных. Множитель 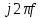 называют оператором дифференцирования сигнала в частотной области. называют оператором дифференцирования сигнала в частотной области.Свойство интегрирования сигнала во временной области. Интегрирование, как известно, является операцией, обратной дифференцированию. Поэтому, исходя из результатов, полученных в предыдущем разделе, казалось бы, можно ожидать следующий результат: если выполняется равенство 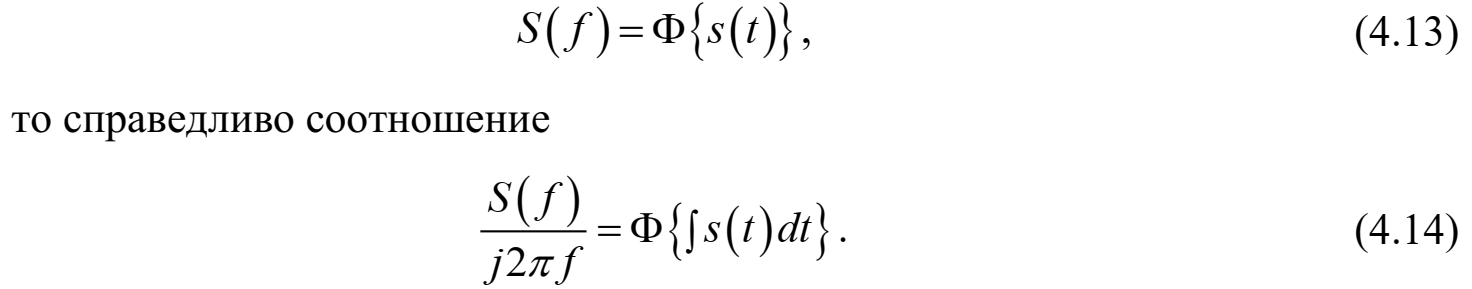 Спектр интеграла получается путем деления спектра исходного сигнала на 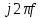 . Однако все не так просто. Детальный анализ показывает, что эта формула справедлива лишь для сигналов, не содержащих постоянной составляющей, у которых . Однако все не так просто. Детальный анализ показывает, что эта формула справедлива лишь для сигналов, не содержащих постоянной составляющей, у которых В общем же случае, результат должен содержать дополнительное слагаемое в виде дельта-функции на нулевой частоте. Множитель перед дельта-функцией пропорционален постоянной составляющей сигнала: 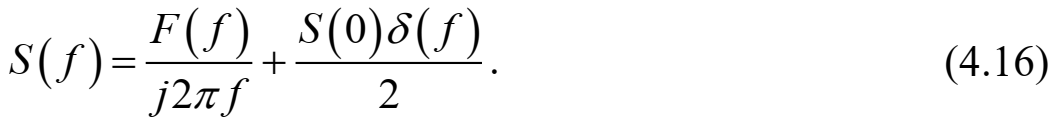 Итак, при интегрировании исходного сигнала высокие частоты ослабляются, а низкие усиливаются. Фазовый спектр сигнала смещается на –90° для положительных частот и на 90° для отрицательных. Множитель 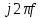 называют оператором интегрирования в частотной области. называют оператором интегрирования в частотной области.Свойство спектра свертки сигналов. Если выполняются равенства: 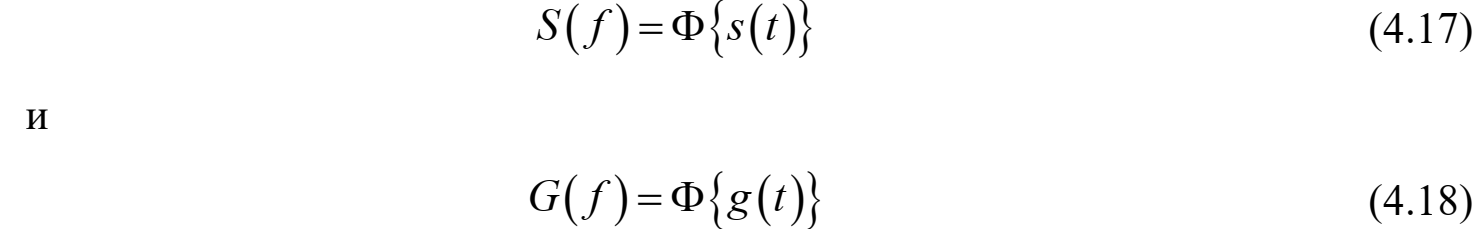 то справедливо соотношение (теорема Планшераля)  Полученный результат очень важен, он часто используется на практике: спектр свертки сигналов равен произведению их спектров. Свойство спектра произведения сигналов. Если выполняются равенства:  Как и следовало ожидать, спектр произведения сигналов представляет собой свертку их спектров. Свойство умножения сигнала на множитель  . Если выполняется равенство . Если выполняется равенството справедливо соотношение Таким образом, при умножения сигнала на множитель  спектр результата смещается вправо по оси частот на спектр результата смещается вправо по оси частот на 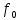 . .Свойство умножения сигнала на множитель t. Если выполняется равенство 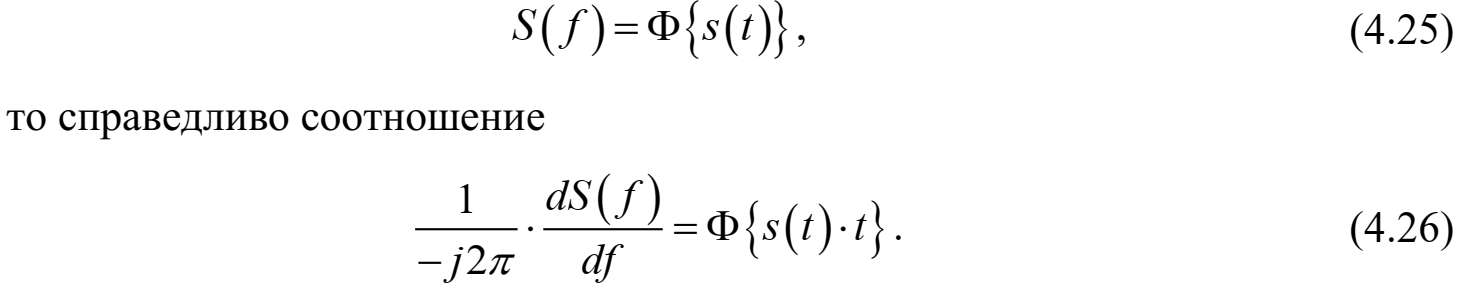 Таким образом, при умножения сигнала на множитель t спектр результата подвергается дифференцированию по частоте и умножению на множитель 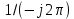 . .В лабораторной работе необходимо получить экспериментальное подтверждения основных свойств преобразования Фурье. Оборудование и материалы Аппаратура. Для выполнения лабораторной работы необходим персональный компьютер. Программное обеспечение. Для выполнения лабораторной работы необходима операционная система WINDOWS, программа Mathcad 10 и выше. Указания по технике безопасности При выполнении лабораторной работы запрещается: - самостоятельно производить ремонт персонального компьютера, а также установку и удаление имеющегося программного обеспечения; - нарушать общепринятые правила техники безопасности при работе с электрооборудованием, в частности, касаться электрических розеток металлическими предметами и т.д.; - принимать пищу, напитки и сорить на рабочем месте пользователя персонального компьютера. В случае неисправности персонального компьютера необходимо немедленно сообщить об этом обслуживающему персоналу лаборатории (системному администратору, оператору). Указания по порядку выполнения работы Методику выполнения работы рассмотрим на следующем примере. Заданы два сигнала  (t) и (t) и  (t). Сигнал (t). Сигнал  (t), представляющий собой отрезок синусоиды с амплитудой U = 2 В, обращающейся в нуль на концах отрезка времени [0, τ], где τ = 1 мс = (t), представляющий собой отрезок синусоиды с амплитудой U = 2 В, обращающейся в нуль на концах отрезка времени [0, τ], где τ = 1 мс = 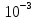 с. Аналитическое описание сигнала представлено формулой с. Аналитическое описание сигнала представлено формулой Сигнал  (t) представляет собой прямоугольный импульс высотой A = 1,5 В и длительностью τ = 1 мс. (t) представляет собой прямоугольный импульс высотой A = 1,5 В и длительностью τ = 1 мс.Требуется для сигналов  (t) и (t) и  (t) подтвердить: (t) подтвердить:- линейность преобразования Фурье; - свойство задержки сигнала во времени; - свойство изменения масштаба оси времени; - свойство дифференцирования и интегрирования сигнала вовременной области; - свойства спектра свертки сигналов (теоремы Планшераля). Рассмотрим решение поставленной задачи в математическом пакете Mathcad: Запускаем Mathcad. Согласно (4.15) и заданным параметрам вводим математическое определение сигнала  (t) и строим его график (рисунок 4.1). (t) и строим его график (рисунок 4.1). Рисунок 4.1 – Определение и график сигнала s1(t) 2. Согласно заданным параметрам, вводим определение второго сигнала  (t) (t)  и строим его график (рисунок 4.2). и строим его график (рисунок 4.2). Рисунок 4.2 – Определение и график сигнала  (t) (t) 3. Подтвердим линейность преобразования Фурье. Определяем спектральные функции сигналов  (t) и (t) и  (t) (рисунок 4.3). (t) (рисунок 4.3). Рисунок 4.2 – Определение спектральных функций сигналов  (t) и (t) и  (t) (t) 4. Суммируем спектральные функции сигналов  (t) и (t) и  (t), находим модуль и аргумент суммы спектральных функций сигналов (t), находим модуль и аргумент суммы спектральных функций сигналов  (t) и (t) и  (t), строим графики амплитудного и фазового спектров суммы спектральных функций сигналов (t), строим графики амплитудного и фазового спектров суммы спектральных функций сигналов  (t) и (t) и  (t) (рисунки 4.3 и 4.4). (t) (рисунки 4.3 и 4.4).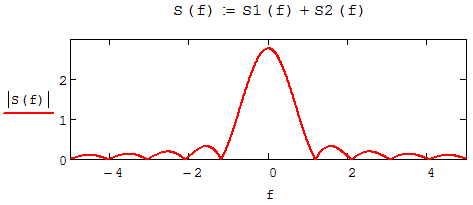 Рисунок 4.3 – Амплитудный спектр суммы спектральных функций сигналов  (t) и (t) и  (t) (t) 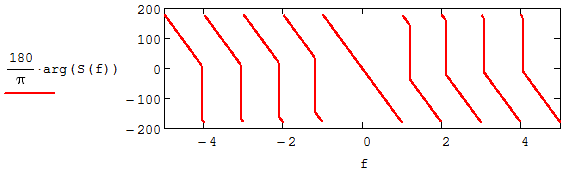 Рисунок 4.4 – Фазовый спектр суммы спектральных функций сигналов  (t) и (t) и  (t) (t)5. Вычисляем суммарный сигнал sΣ(t) =  (t) + (t) + (t) и строим его график (t) и строим его график(рисунок 4.5). 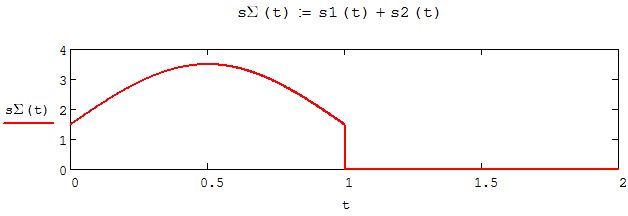 Рисунок 4.5 – Определение и график сигнала sΣ(t) =  (t) + (t) + (t) (t) 6. Определяем спектральную функцию суммарного сигнала sΣ(t) =  (t) + (t) + (t) (рисунок 4.6). (t) (рисунок 4.6). Рисунок 4.6 – Определение спектральной функции суммарного сигнала sΣ(t) =  (t) + (t) + (t) (t) 7. Находим модуль и аргумент спектральной функции суммарного сигнала sΣ(t) =  (t) + (t) + (t) и строим графики его амплитудного и фазового спектров (рисунки 4.7 и 4.8). (t) и строим графики его амплитудного и фазового спектров (рисунки 4.7 и 4.8). Рисунок 4.6 – Амплитудный спектр суммарного сигнала sΣ(t) =  (t) + (t) + (t) (t)  Рисунок 4.7 – Фазовый спектр суммарного сигнала sΣ(t) = s1(t) + s2(t) Сравнивая между собой амплитудный спектр суммы спектральных функций (рисунок 4.3) и амплитудный спектр суммарного сигнала sΣ(t)=  (t) + (t) + (t) (рисунок 4.6), а также фазовый спектр суммы спектральных функций сигналов (t) (рисунок 4.6), а также фазовый спектр суммы спектральных функций сигналов  (t) + (t) + (t) (рисунок 4.4) и фазовый спектр суммарного сигнала sΣ(t) = (t) (рисунок 4.4) и фазовый спектр суммарного сигнала sΣ(t) =  (t) + (t) + (t) (рисунок 4.7) убеждаемся в том, что они совпадают. (t) (рисунок 4.7) убеждаемся в том, что они совпадают.Следовательно, справедливость линейности преобразования Фурье на основе эксперимента доказана. 8. Подтвердим свойство задержки сигнала во времени, например, для сигнала  (t). Будем считать, что задержка сигнала составляет одну пятую его длительности, т. е. (t). Будем считать, что задержка сигнала составляет одну пятую его длительности, т. е.  . Введем в рассмотрение новый сигнал . Введем в рассмотрение новый сигнал  . Задаем математическое определение сигнала x(t) и строим его график (рисунок 4.8). . Задаем математическое определение сигнала x(t) и строим его график (рисунок 4.8). Рисунок 4.8 – Определение и график сигнала x(t) 9. Определяем спектральную функцию сигнала x(t) (рисунок 4.9).  Рисунок 4.9 – Определение спектральной функции сигнала x(t) Находим модуль и аргумент спектральной функции сигнала x(t) и строим графики его амплитудного и фазового спектров (рисунки 4.10 и 4.11).  Рисунок 4.10 – Амплитудный спектр сигнала x(t)  Рисунок 4.11 – Фазовый спектр сигнала x(t) Согласно (4.7) умножаем спектральную функцию 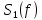 сигнала сигнала 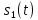 на множитель на множитель 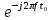 и получившийся результат обозначаем, как и получившийся результат обозначаем, как  (рисунок 4.12). (рисунок 4.12).Рисунок 4.12 – Умножаем спектральную функцию  сигнала сигнала 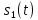 на намножитель 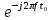 12. Находим модуль и аргумент спектральной функции  и строим их графики (рисунки 4.13 и 4.14). и строим их графики (рисунки 4.13 и 4.14).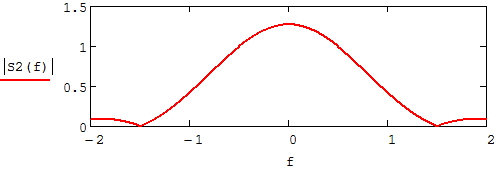 Рисунок 4.13 – Модуль спектральной функции   Рисунок 4.14 – Аргумент спектральной функции  Сравнивая между собой амплитудный спектр сигнала x(t) (рисунок 4.10) и модуль спектральной функции  (рисунок 4.13), а также фазовый спектр сигнала x(t) (рисунок 4.11) и аргумент спектральной функции (рисунок 4.13), а также фазовый спектр сигнала x(t) (рисунок 4.11) и аргумент спектральной функции  (рисунок 4.14) убеждаемся в том, что они совпадают. Следовательно, справедливость свойства задержки сигнала во времени для преобразования Фурье на основе эксперимента доказана. (рисунок 4.14) убеждаемся в том, что они совпадают. Следовательно, справедливость свойства задержки сигнала во времени для преобразования Фурье на основе эксперимента доказана.Подтвердим свойство изменения масштаба оси времени, например, для сигнала  . Будем считать, что коэффициент изменения масштаба оси времени составляет два, т. е. α = 2. Введем в рассмотрение новый сигнал x(t) = . Будем считать, что коэффициент изменения масштаба оси времени составляет два, т. е. α = 2. Введем в рассмотрение новый сигнал x(t) =  . Задаем математическое определение сигнала x(t) и строим его график (рисунок 4.15). . Задаем математическое определение сигнала x(t) и строим его график (рисунок 4.15). Рисунок 4.15 – Определение и график сигнала x(t) Определяем спектральную функцию сигнала x(t) (рисунок 4.16).  Рисунок 4.16 – Определение спектральной функции сигнала x(t) Находим модуль и аргумент спектральной функции сигнала x(t) и строим графики его амплитудного и фазового спектров (рисунки 4.17 и 4.18).  Согласно (4.9) умножаем спектральную функцию  сигнала сигнала  на множитель на множитель  , изменяем масштаб оси частот, путем деления частоты на коэффициент изменения масштаба оси времени α и получившийся результат обозначаем, как , изменяем масштаб оси частот, путем деления частоты на коэффициент изменения масштаба оси времени α и получившийся результат обозначаем, как  (рисунок 4.19). (рисунок 4.19).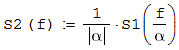 Рисунок 4.19 – Умножаем спектральную функцию 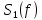 сигнала сигнала 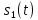 на множитель на множитель  и изменяем масштаб оси частот и изменяем масштаб оси частотНаходим модуль и аргумент спектральной функции  и строим их графики (рисунки 4.20 и 4.21). и строим их графики (рисунки 4.20 и 4.21). Сравнивая между собой амплитудный спектр сигнала x(t) (рисунок 4.17) и модуль спектральной функции  (рисунок 4.20), а также фазовый спектр сигнала x(t) (рисунок 4.18) и аргумент спектральной функции (рисунок 4.20), а также фазовый спектр сигнала x(t) (рисунок 4.18) и аргумент спектральной функции  (рисунок 4.21) убеждаемся в том, что они совпадают. Следовательно, справедливость свойства изменения масштаба оси времени для преобразования Фурье на основе эксперимента доказана. (рисунок 4.21) убеждаемся в том, что они совпадают. Следовательно, справедливость свойства изменения масштаба оси времени для преобразования Фурье на основе эксперимента доказана.Подтвердим свойство дифференцирования сигнала во временной области, например, для сигнала  . Выполним дифференцирование сигнала . Выполним дифференцирование сигнала  во временной области и введем в рассмотрение новый сигнал во временной области и введем в рассмотрение новый сигнал  . Задаем математическое определение сигнала x(t) и строим его график (рисунок 4.22). . Задаем математическое определение сигнала x(t) и строим его график (рисунок 4.22).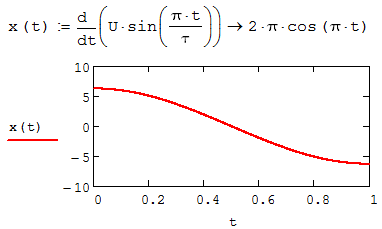 Рисунок 4.22 – Определение и график сигнала x(t) Определяем спектральную функцию сигнала x(t) (рисунок 4.23). 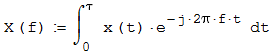 Рисунок 4.23 – Определение спектральной функции сигнала x(t) Находим модуль и аргумент спектральной функции сигнала x(t) и строим графики его амплитудного и фазового спектров (рисунки 4.24 и 4.25). 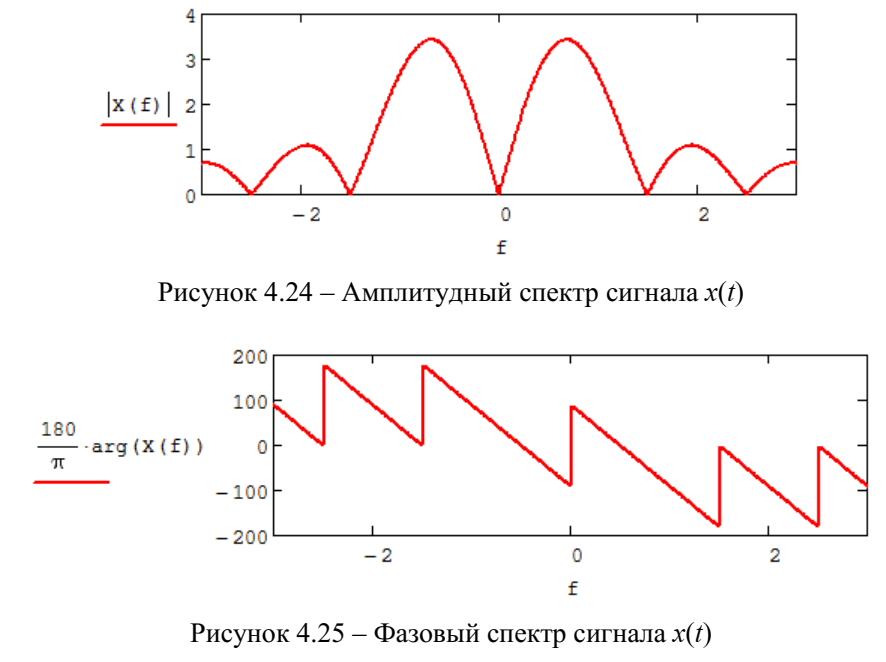 Согласно (4.12) умножаем спектральную функцию  сигнала сигнала  на множитель на множитель  и получившийся результат обозначаем, как и получившийся результат обозначаем, как  (рисунок 4.26). (рисунок 4.26).Рисунок 4.26 – Умножаем спектральную функцию  сигнала сигнала  на намножитель  22. Находим модуль и аргумент спектральной функции  и строим их графики (рисунки 4.27 и 4.28) и строим их графики (рисунки 4.27 и 4.28) Сравнивая между собой амплитудный спектр сигнала x(t) (рисунок 4.24) и модуль спектральной функции  (рисунок 4.27), а также фазовый спектр сигнала x(t) (рисунок 4.25) и аргумент спектральной функции (рисунок 4.27), а также фазовый спектр сигнала x(t) (рисунок 4.25) и аргумент спектральной функции  (рисунок 4.28) убеждаемся в том, что они совпадают. Следовательно, справедливость свойства дифференцирования сигнала во временной области для преобразования Фурье на основе эксперимента доказана. (рисунок 4.28) убеждаемся в том, что они совпадают. Следовательно, справедливость свойства дифференцирования сигнала во временной области для преобразования Фурье на основе эксперимента доказана.Подтвердим свойство интегрирования сигнала во временной области. При этом следует учитывать, что для интегрированного сигнала преобразование Фурье может и не существовать, если интеграл Фурье расходится (соответственно в частотной области для нулевой частоты мы будем иметь деление бесконечно большого числа на 0). Для исключения этого воспользуемся сигналом, интеграл которого имеет нулевую постоянную составляющую. Для этого в формуле (4.27) для сигнала  заменим функцию синуса косинусом, того же аргумента: заменим функцию синуса косинусом, того же аргумента: Согласно формуле (4.28) и заданным параметрам вводим математическое определение сигнала 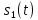 и строим его график (рисунок 4.29). и строим его график (рисунок 4.29).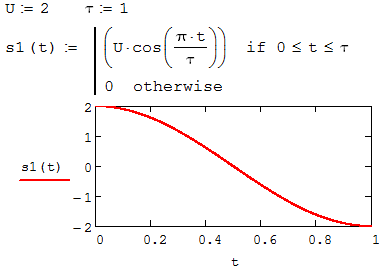 Рисунок 4.29 – Определение и график сигнала s1(t) согласно формуле (4.28) Выполним интегрирования сигнала 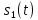 , заданного соотношением (4.28) во временной области и введем в рассмотрение новый сигнал x(t) = , заданного соотношением (4.28) во временной области и введем в рассмотрение новый сигнал x(t) =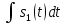 . Задаем математическое определение сигнала x(t) и строим его график (рисунок 4.30). . Задаем математическое определение сигнала x(t) и строим его график (рисунок 4.30). Рисунок 4.30 – Определение и график сигнала x(t) Определяем спектральную функцию сигнала x(t) (рисунок 4.31).  Рисунок 4.31 – Определение спектральной функции сигнала x(t) Находим модуль и аргумент спектральной функции сигнала x(t) и строим графики его амплитудного и фазового спектров (рисунки 4.32 и 4.33).  27. Согласно (4.14) делим спектральную функцию  сигнала сигнала  на на  и получившийся результат обозначаем, как и получившийся результат обозначаем, как  (рисунок 4.34). (рисунок 4.34).Рисунок 4.34 – Делим спектральную функцию  сигнала сигнала  на на  28. Находим модуль и аргумент спектральной функции  и строим их графики (рисунки 4.35 и 4.36). и строим их графики (рисунки 4.35 и 4.36). Сравнивая между собой амплитудный спектр сигнала x(t) (рисунок 4.32) и модуль спектральной функции  (рисунок 4.35), а также фазовый спектр сигнала x(t) (рисунок 4.33) и аргумент спектральной функции (рисунок 4.35), а также фазовый спектр сигнала x(t) (рисунок 4.33) и аргумент спектральной функции  (рисунок 4.36) убеждаемся в том, что они совпадают. Следовательно, справедливость свойства интегрирования сигнала во временной области для преобразования Фурье на основе эксперимента доказана. (рисунок 4.36) убеждаемся в том, что они совпадают. Следовательно, справедливость свойства интегрирования сигнала во временной области для преобразования Фурье на основе эксперимента доказана.29. Подтвердим свойство спектра свертки сигналов (теорема Планшераля): спектр свертки сигналов равен произведению их спектров. Согласно формуле (4.19) находим сигнала x(t) как свертку сигналов  и и  и строим его график (рисунок 4.37). и строим его график (рисунок 4.37). Рисунок 4.37 – Определение и график сигнала x(t) 30. Определяем вещественную и мнимую часть, а также модуль и аргумент спектральной функции сигнала x(t) (рисунок 4.38).  Рисунок 4.38 – Определение вещественной и мнимой части, а также модуля и аргумента спектральной функции сигнала x(t) 31. Строим графики амплитудного и фазового спектров сигнала x(t) (рисунки 4.39 и 4.40).  Рисунок 4.39 – Амплитудный спектр сигнала x(t)  Рисунок 4.40 – Фазовый спектр сигнала x(t) 32. Согласно (4.19) умножаем спектральную функцию  сигнала сигнала  на спектральную функцию на спектральную функцию  сигнала сигнала  и получившийся результат обозначаем, как и получившийся результат обозначаем, как  (рисунок 4.41). (рисунок 4.41).Рисунок 4.41 – умножаем спектральную функцию  сигнала сигнала  на спектральную функцию на спектральную функцию  сигнала сигнала  33. Находим модуль и аргумент спектральной функции S3(f) и строим их графики (рисунки 4.42 и 4.43).  Сравнивая между собой амплитудный спектр сигнала x(t) (рисунок 4.39) и модуль спектральной функции  (рисунок 4.42), а также фазовый спектр сигнала x(t) (рисунок 4.40) и аргумент спектральной функции (рисунок 4.42), а также фазовый спектр сигнала x(t) (рисунок 4.40) и аргумент спектральной функции  (рисунок 4.43) убеждаемся в том, что они совпадают. Следовательно, справедливость свойства спектра свертки сигналов (теоремы Планшераля) для преобразования Фурье на основе эксперимента доказана. (рисунок 4.43) убеждаемся в том, что они совпадают. Следовательно, справедливость свойства спектра свертки сигналов (теоремы Планшераля) для преобразования Фурье на основе эксперимента доказана.Порядок выполнения работы: 54. Запустить Mathcad. 55. Экспериментально подтвердить в программе Mathcad для заданных сигналов  и и  в соответствии с вариантом индивидуального задания (таблица 4.1): в соответствии с вариантом индивидуального задания (таблица 4.1):- линейность преобразования Фурье; - свойство задержки сигнала во времени (только для сигнала  ); );- свойство изменения масштаба оси времени (только для сигнала  ); );- свойство дифференцирования и интегрирования сигнала во временной области (только для сигнала  ); );- свойства спектра свертки сигналов (теоремы Планшераля). 56. Сохранить результаты выполнения индивидуального задания. 57. Сформулировать выводы и оформить отчет по лабораторной работе. 58. Защитить работу. Варианты заданий Номер варианта (таблица 4.1) соответствует номеру фамилии студента в списке учебной группы (подгруппы). Таблица 4.1 – Варианты индивидуальных заданий   Примечание – Графическое и аналитическое определение параметров исследуемых сигналов приведено в таблице 1.1. Содержание отчета Отчет по лабораторной работе оформляется в виде документа Mathcad или Word и должен включать: 59. Названия лабораторной работы. 60. Цель лабораторной работы. 61. Формулировку индивидуального задания и результат его выполнения. 62. Краткие выводы по результатам выполнения лабораторной работы. Контрольные вопросы   |
