Лабораторная работа. ЛБ 6. Лабораторная работа 6 Измерение жёсткости пружины

• Название: Лабораторная работа 6 Измерение жёсткости пружины
• Анкор: Лабораторная работа
• Дата: 26.01.2023
• Размер: 1.83 Mb.
• Имя файла: ЛБ 6.docx
• Тип: Лабораторная работа; #905919

Лабораторная работа № 6

Измерение жёсткости пружины
Цель работы: найти жесткость пружины из измерений удлинения пружины при различных значениях силы тяжести.

Оборудование: штатив с муфтой и лапкой, пружинный динамометр, набор грузов (по 100 г), линейка.
Теоретическая часть

Сила упругости

Любое тело, когда его деформируют и оказывают внешнее воздействие, сопротивляется и стремиться восстановить прежние форму и размеры. Это происходит по причине электромагнитного взаимодействия в теле на молекулярном уровне.

Деформация - изменение положения частиц тела друг относительно друга. Результат деформации - изменение межатомных расстояний и перегруппировка блоков атомов.

Сила упругости - сила, возникающая при деформации в теле и стремящаяся вернуть тело в начальное состояние. 

Рассмотрим простейшие деформации - растяжение и сжатие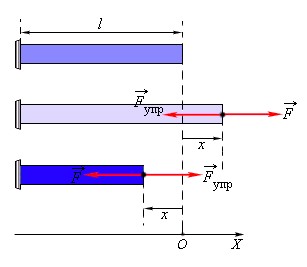 



На рисунке показано, как действует сила упругости, когда мы сжимаем или растягиваем стержень.

Закон Гука

Для малых деформаций  справедлив закон Гука. 

Закон Гука

Деформация, возникающая в упругом теле, пропорциональна приложенной к телу силе. 

F_упр=−kx

Здесь k - коэффициент пропорциональности, называемый жесткостью. Единица измерения жесткости системе СИ Ньютон на метр. Жесткость зависит от материала тела, его формы и размеров.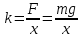



Знак минус показывает, что сила упругости противодействует внешней силе и стремится вернуть тело в первоначальное состояние. 

Следует иметь в виду, что закон Гука выполняется только при малых деформациях. При превышении предела пропорциональности связь между напряжениями и деформациями становится нелинейной. Для многих сред закон Гука неприменим даже при малых деформациях.
Практическая часть

1. 
   Закрепите на штативе конец спиральной пружины (другой конец пружины снабжен стрелкой-указателем и крючком — рис. 176).
   
2. 
   Рядом с пружиной или за ней установите и закрепите линейку с миллиметровыми делениями.
   
3. 
   Отметьте и запишите то деление линейки, против которого приходится стрелка-указатель пружины.
   

4. 
   Подвесьте к пружине груз известной массы и измерьте вызванное им удлинение пружины.
   
5. 
   К первому грузу добавьте второй, третий и т. д. грузы, записывая каждый раз удлинение |х| пружины. По результатам измерений заполните таблицу:
   

№	m,кг	F=mg, Н	, м	k,Н/м
1
2
3
4

6. 
   Вычислите коэффициент жесткости k.(до сотых)
   
7. 
   Вычислите среднее значение k: _{(округлить до целого числа)}
   
8. 
   Вычислите погрешность измерения первого груза ɛ_k:
   

Приняв за ∆m=0,002 кг, ∆g=0,02 м/с², ∆х=0,0005 м.

9. 
   Найдите ∆k:
   

(округлить до тысячных)

10. 
    Ответ запишите виде: ∆k₁=(k_средн.±ɛ_k) Н/м
    
11. 
    Сделайте вывод по цели работы.
    

Письменно ответьте на вопросы:

1. 
   Груз массой m, подвешенный на пружине жесткостью k, растягивает пружину на Δl. Как изменится жесткость пружины, удлинение, сила упругости, если массу груза увеличить в 2 раза? К каждой позиции левого столбца подберите соответствующую позицию правого и запишите ответ в виде буква-цифра
   

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ ИХ ИЗМЕНЕНИЕ

А) жесткость 1) не изменяется

Б) удлинение 2) увеличивается

В) сила упругости 3) уменьшается

2.