ОПРЕДЕЛЕНИЕ МОДУЛЯ УПРУГОСТИ (МОДУЛЯ ЮНГА) ПО ДЕФОРМАЦИИ ИЗГИБА. Физон 10. Определение модуля упругости (модуля юнга) по деформации изгиба
 Скачать 0.69 Mb. Скачать 0.69 Mb.
|
|
ПЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ РОССИИ
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное бюджетное образовательное учреждение высшего образования «САНКТ-ПЕТЕРБУРГСКИЙ ГОРНЫЙ УНИВЕРСИТЕТ» Кафедра общей и технической физики МЕХАНИКА ЛАБОРАТОРНАЯ РАБОТА № 10 «ОПРЕДЕЛЕНИЕ МОДУЛЯ УПРУГОСТИ (МОДУЛЯ ЮНГА) ПО ДЕФОРМАЦИИ ИЗГИБА»Выполнил: студент группы ПГС-21-2 __________ /Лиева И.К./ (подпись) (Ф.И.О.) Проверил : _______________ __________ /______________/ (подпись) (Ф.И.О.) Санкт-Петербург 2021 год Цель работы: определить модуль Юнга материала путем измерения прогиба стержня при механической нагрузке. Краткое теоретическое содержание:Явление, изучаемое в работе: деформация твердых тел, упругость твердых тел Определение основных физических понятий процессов, величин: деформация - это изменение взаимного положения частиц тела, связанное с их перемещением друг относительно друга за счет приложения усилия (тело искажает форму) модуль упругости - способность твердого тела упруго деформироваться при приложении к нему силы Законы и соотношения: Закон Гука - деформация, возникающая в упругом теле (пружине, стержне, консоли, балке и т. д.), пропорциональна приложенной к этому телу силе Модуль Юнга - измерение прогиба стержней (балок) под действием различных по величине нагрузок F, приложенных в центре стержней (балок), лежащих на опорах A и B, которые расположены на фиксированном расстоянии L друг от друга 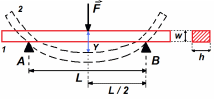 Схематическое изображение деформации балки методом изгиба. 1 - недеформированная балка, 2 - деформированная балка, A и B - точки опоры, F - нагрузка Основные расчетные формулы: Модуль Юнга 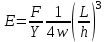 Е - модуль Юнга, величина, определяющая упругие свойства материала, из которого изготовлен образец[H/м2] F - приложенная в центре стержня сил [H] w и h - размеры поперечного сечения стержня [м] γ - стрела прогиба стержня под нагрузкой [м] L - расстояние между опорами балки [мм] Закон Гука F = kl k – постоянная величина для данного образца [H/м] l – величина абсолютной деформации [м] F - сила упругости [H] При упругой деформации пропорционально силе, приходящейся на единицу площади поперечного сечения стержня. Закон Гука в этом случае можно записать в виде: 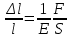 или или 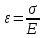 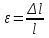 - деформация или относительное изменение длины стержня - деформация или относительное изменение длины стержня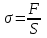 - нормальное механическое напряжение - нормальное механическое напряжение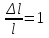 . .l - длина стержня [м] l – величина абсолютной деформации [м] ε - относительное удлинение [--] σ - нормальное механическое напряжение [Па] F - сила действующая на единицу площади [H] S - единица площади поперечного сечения стержня [м] E – коэффициент пропорциональности, который называется модулем упругости (модулем Юнга) Приборы:
Исходные данные: m1= 0,2 кг m2= 0,2 кг m3= 0,3 кг m4= 0,51кг m5= 0,251кг l = 0,4 м Погрешность прямых измерений: h= 0,05мм w=0,05мм l=1мм m= 0,5г γ = 0,01мм Схема установки:    Стержень из исследуемого материала Две призмы, обращенные рабочими концами вверх Серьга Платформа Индикатор Груз Погрешность: 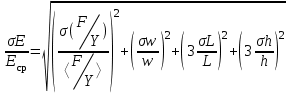 Расчетная часть: Таблица 1
Таблица 2
Увеличение и уменьшение нагрузки стержня: 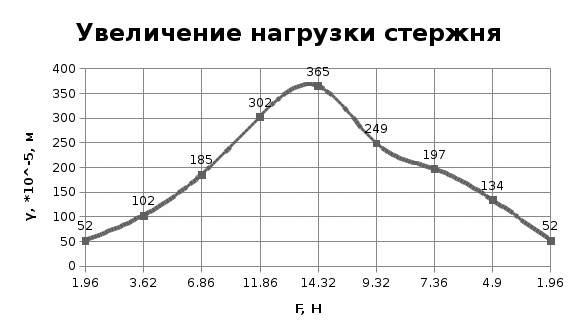 Примеры вычислений: 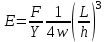 = = 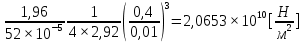 Еср= 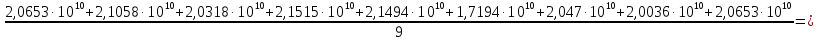 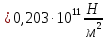 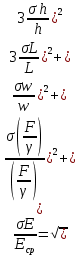 = 0,076 = 0,076σE=Eср·0,076=0,02·1011 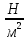 Е= 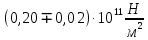 Вывод: Исходя из полученной величины модуля Юнга, определим, что исследуемый материал – сталь |

