жж. Лабораторная работа 6 Изучение вращательного движения твердого тела вокруг неподвижной оси на примере маятника Обербека
 Скачать 377 Kb. Скачать 377 Kb.
|
|
Министерство Общего и Специального Образования Обнинский Государственный Технический Университет Атомной ЭнергетикиЛабораторная работа №6 «Изучение вращательного движения твердого тела вокруг неподвижной оси на примере маятника Обербека» Выполнил: Прокофьев А. С. Проверил: Вишератин К. Н. Обнинск 2002 Цель работы: изучение вращательного движения на примере маятника Обербека. Задание 1. Экспериментальная проверка основного уравнения вращательного движения, определение момента инерции системы и оценка влияния момента силы трения. Время падения груза, массой m Таблица1
I. По формуле II. По формуле Sn= 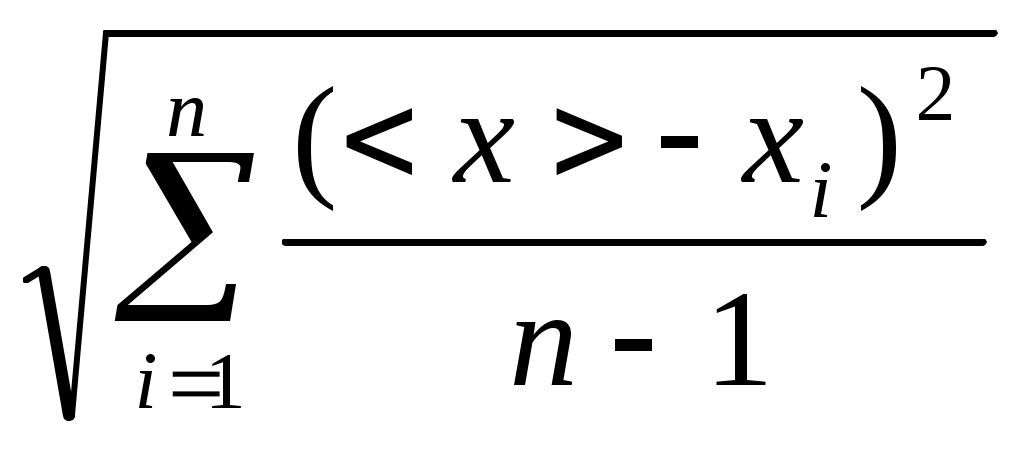 и S= и S=III. По формуле  ( (IV. По формуле 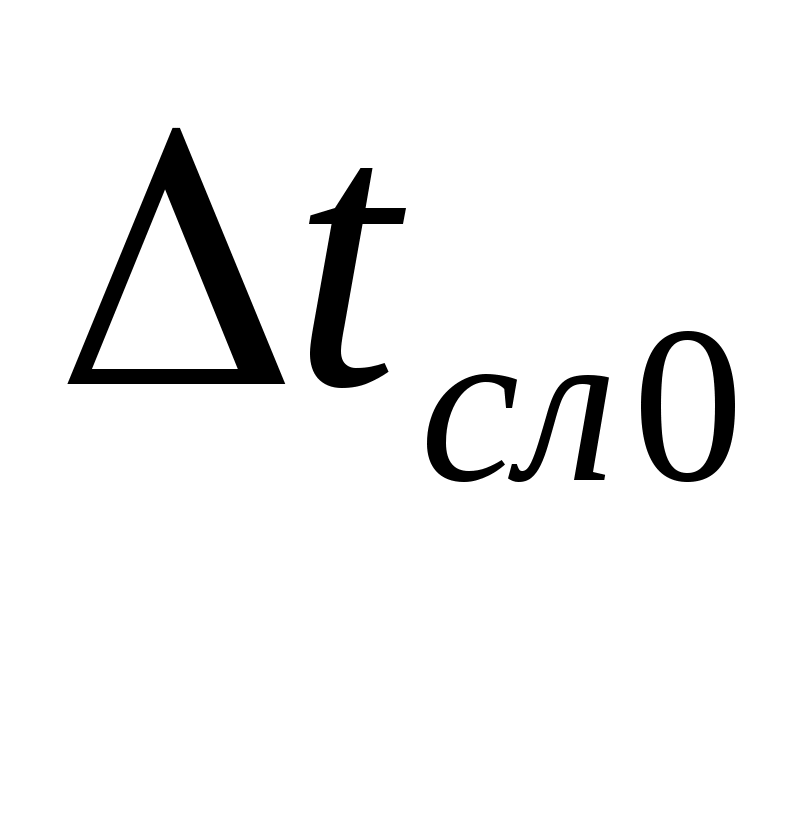 =4,3*0,007=0,030(c) => =4,3*0,007=0,030(c) => 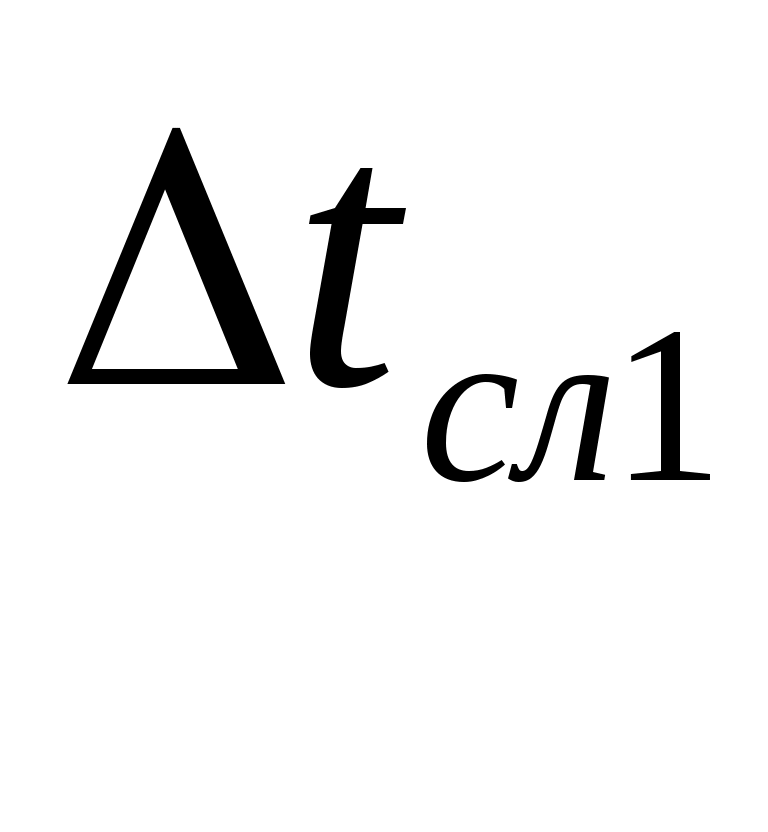 =4,3*0,006=0,026(c) => =4,3*0,006=0,026(c) => 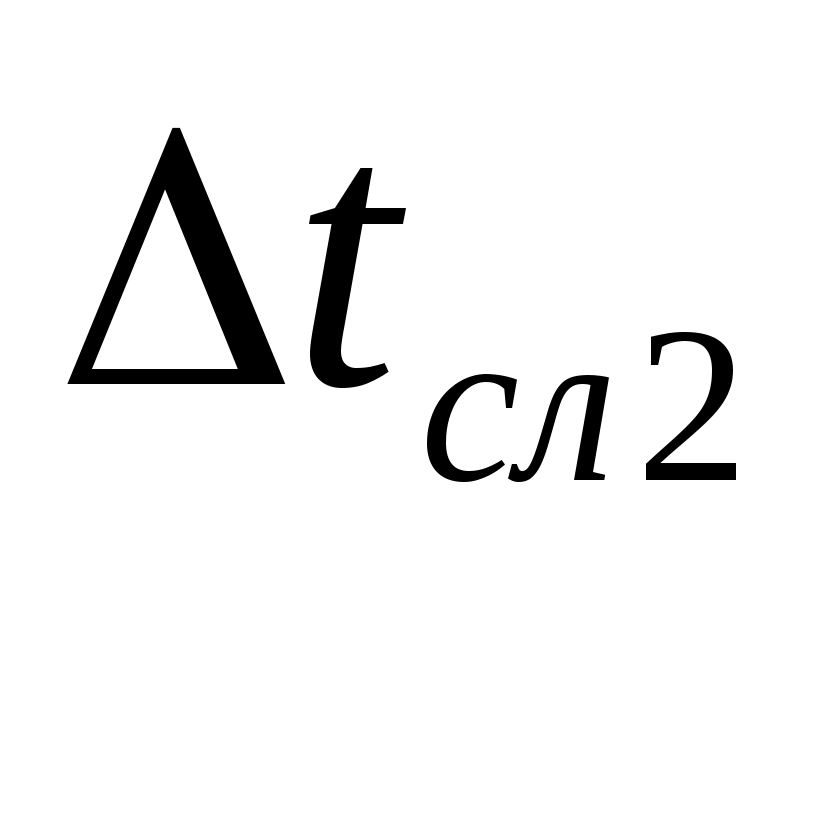 =4,3*0,021=0,090 (c) => =4,3*0,021=0,090 (c) => V. По формуле < VI. По формуле 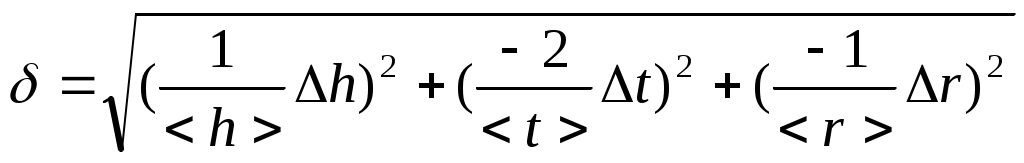 = =r=2(мм) т.е.: VII. По формуле VIII. По формуле <N0>=58,3 <N1>=58,3 <N2>=58,3 IX. По формуле 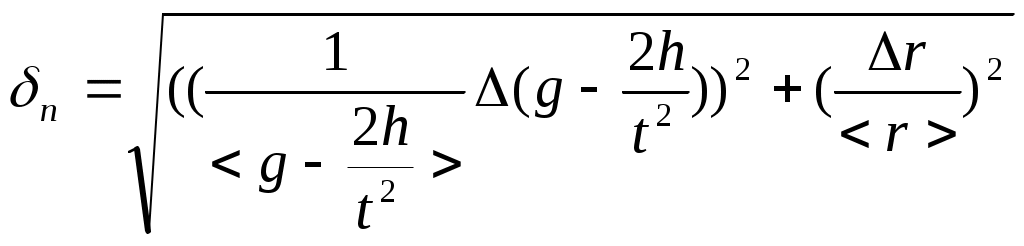 = =(g- N0=(25 N1=(24 N2=(23 Как видно из графика №1 Nтр J=ctg 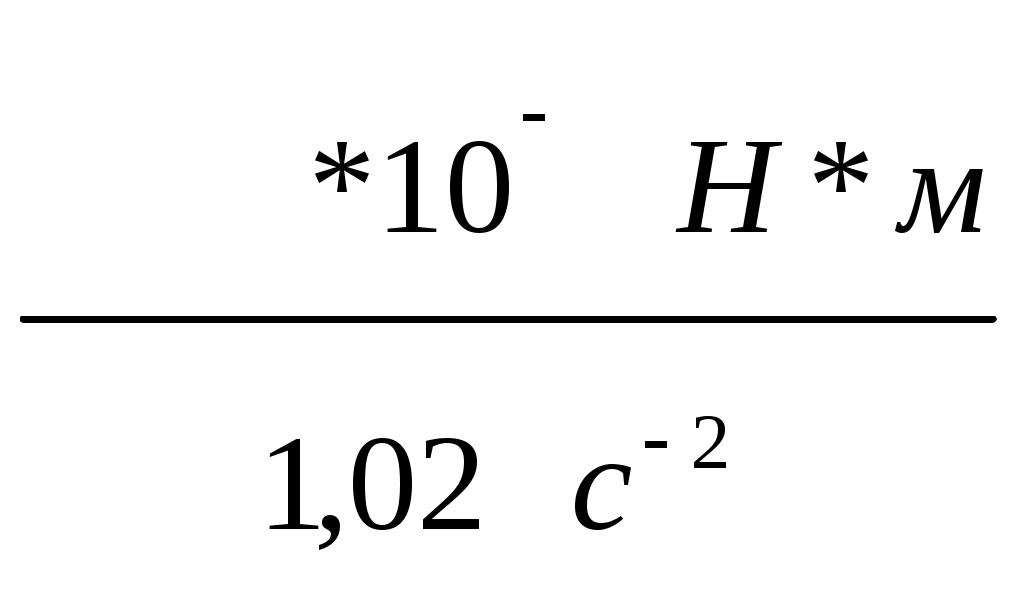 = Н = НЗадание 2. Проверка теоремы Штейнера. Таблица2: Время движения платформы (без грузов)
По формуле J=Mr2( I. Для этого определяем среднее время и его погрешности: h=(400 II. Определяем моменты инерции. <J1>=58,3 <J2>=58,3 III. По формуле 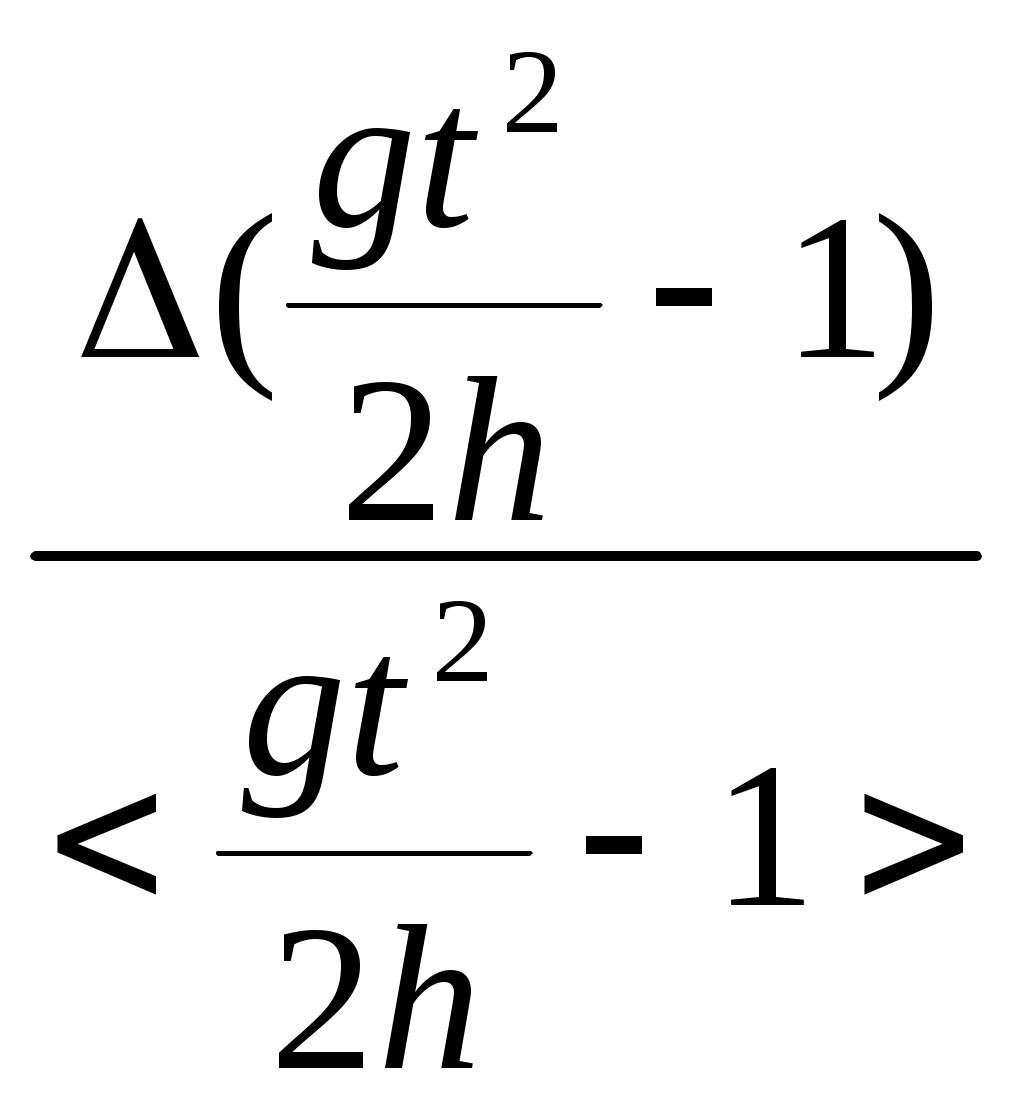 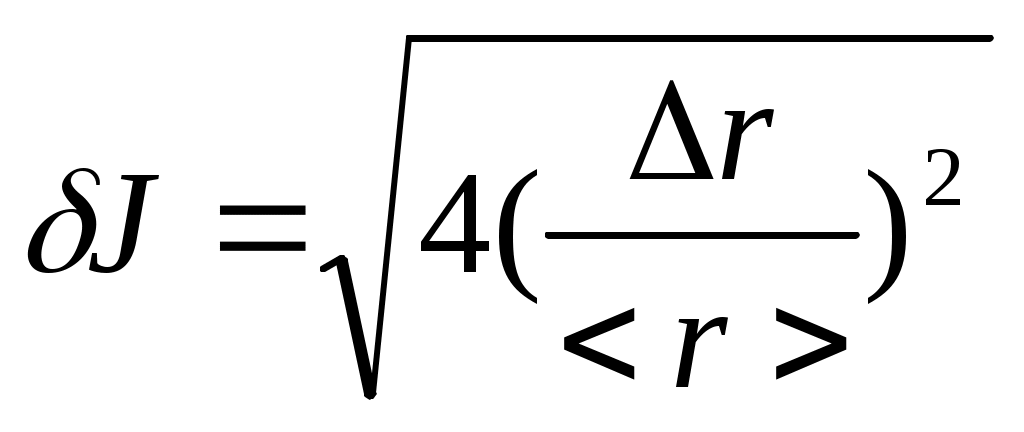 =2 =2т.е. Итак моменты инерции равны: J1=0,05 J2=0,04 IV. Как видно из графика №2 J(0) = Н*м*с2 Таблица3:Время движения платформы при снятых грузах m:
V. Определяю среднее время и его пегрешность: VI. Определим момент инерции Jкр маятника без грузов m: <Jкр>=58,3 т.е. Jкр=0,007 Т.к. по теореме Штейнера J=J(0)+4mR2 J(0)=Jкр+4J0 J(0)=0,7 VII. По формуле найдем J0 – момент инерции груза массой m относительно оси, проходящей через его центр масс и параллельной оси, вокруг которой вращается маятик. J0= Н ВЫВОД: В первом задании при построении графика экспериментальной точки, в пределах точности измерений, “легли” на прямую. Это подтверждает зависимость Из графика было найдено J= Н Во втором задании были определены моменты инерции тела J1и J2. Был построен график зависимости J(R), причем как в первом задании, график-прямая, т.е. подтверждается зависимость J=J(0)+4mR2. А также из графика было найдено J(0) График к заданию №1. 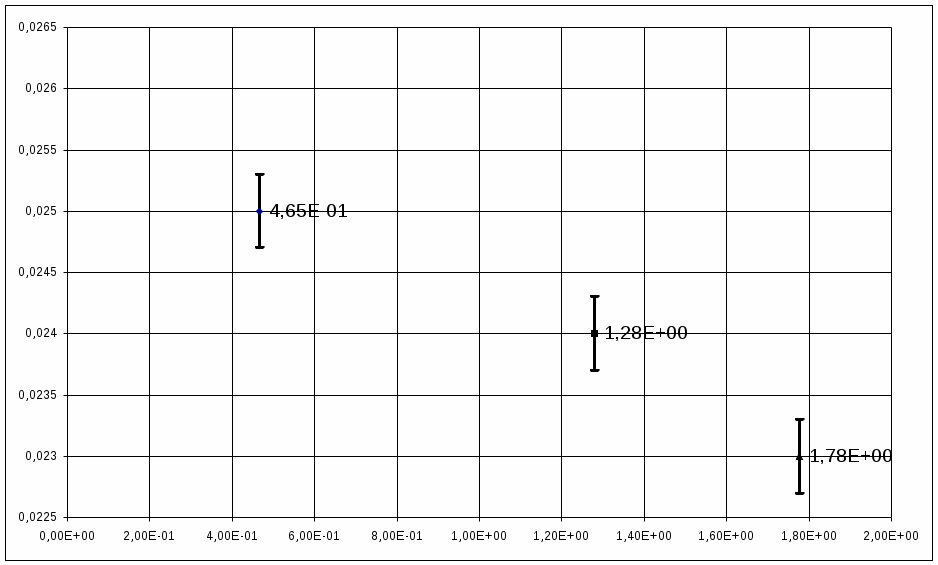 График зависимости I = 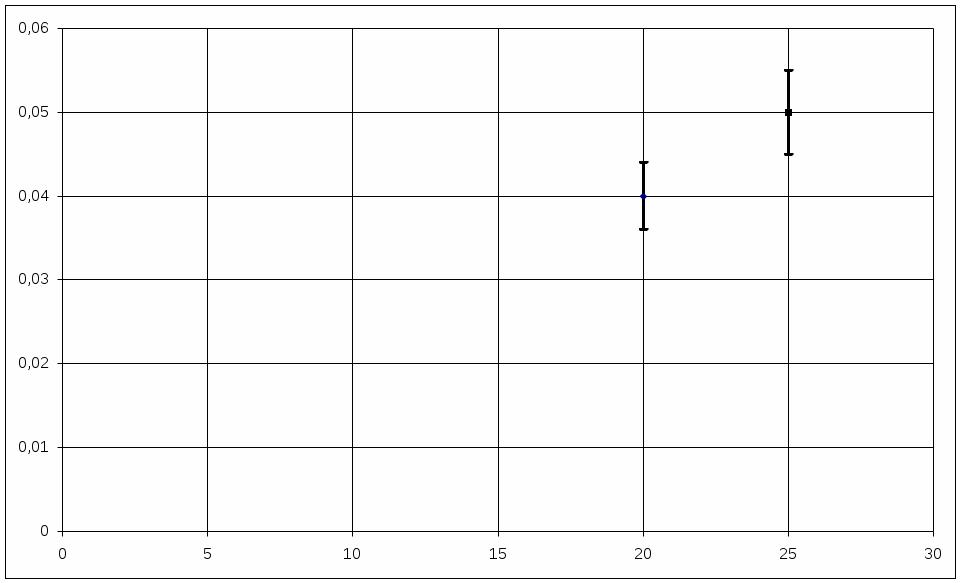 |

 ,c
,c