Лабораторная работа 6 Обербек. Лабораторная работа 6 Определение момента инерции с помощью маятника Обербека студент группы
 Скачать 238.93 Kb. Скачать 238.93 Kb.
|
|
ПЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДНИЕ РОССИИ  МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное бюджетное образовательное учреждение высшего образования «САНКТ-ПЕТЕРБУРГСКИЙ ГОРНЫЙ УНИВЕРСИТЕТ» Кафедра общей и технической физики Лабораторная работа №6 Определение момента инерции с помощью маятника Обербека Выполнил:
Дата: Проверил:
Санкт-Петербург 2022 Цель работы Исследовать зависимость момента инерции крестовины с надетыми на нее грузиками от распределения массы относительно оси вращения, проходящей через центр масс. Явление, изучаемое в работе: вращательное движение твердого тела. Краткое теоретическое содержание В основе эксперимента лежит основное уравнение динамики вращательного движения твердого тела 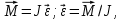 где М - суммарный момент внешних сил, приложенных к телу относительно оси вращения; J - момент инерции тела относительно той же оси; e - угловое ускорение. В динамике вращательного движения различают два понятия: момент силы относительно точки и момент силы относительно оси вращения. где М - суммарный момент внешних сил, приложенных к телу относительно оси вращения; J - момент инерции тела относительно той же оси; e - угловое ускорение. В динамике вращательного движения различают два понятия: момент силы относительно точки и момент силы относительно оси вращения.Вращательное движение твердого тела - явление, при котором во время вращения твердого тела все его точки движутся по окружностям, центры которых лежат на одной прямой, называемой осью вращения. Момент инерции — скалярная физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Момент силы - векторная физическая величина, равная векторному произведению радиус-вектора, проведенного от оси вращения к точке приложения силы, на вектор этой силы. Момент силы относительно оси вращения – проекция вектора момента силы относительно точки M на произвольную ось z, которая проходит через точку О. Основные физические законы и соотношения Второй закон Ньютона для поступательного движения тела (m=const). Сумма внешних сил, приложенных к телу: 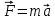 Где m- масса тела, 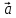 – линейное ускорение тела. – линейное ускорение тела.Основное уравнение динамики вращательного движения твердого тела. Суммарный момент внешних сил, приложенных к телу относительно оси вращения: 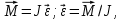 где J - момент инерции тела относительно той же оси; 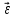 - угловое ускорение. [M]=н*м, [J]=кг*м2, [ - угловое ускорение. [M]=н*м, [J]=кг*м2, [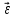 ]=рад/с2 ]=рад/с2Схема установки 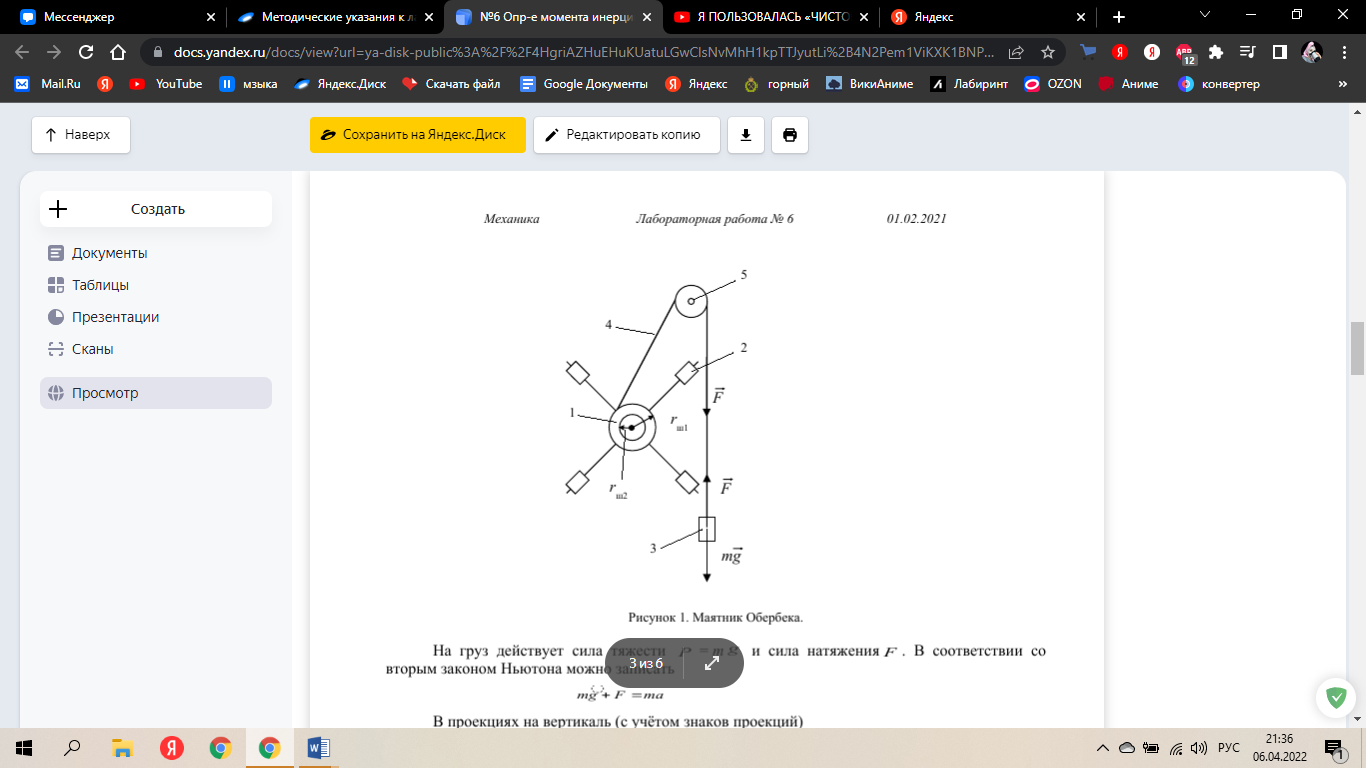 1-крестовина; 2-грузы; 3-груз, массой m; 4-нить; 5-блок. Основные расчётные формулы Момент инерции тела: 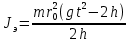 , ,где h - путь, пройденный грузом за время t, м; g- ускорение свободного падения, 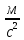 ; ;r0 - радиус шкива, м; m- масса груза, кг. Теоретическое значение момента инерции крестовины: 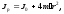 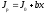 , ,где J0 – момент инерции крестовины без грузов, 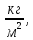 r2 = х и 4m’=b r2 = х и 4m’=b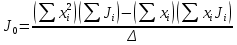  где 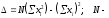 число опытов; число опытов; Ji - экспериментальное значение момента инерции Jэ, 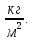 Дисперсия результата измерения момента инерции: 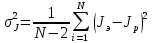 Формула для расчета погрешностей косвенных измерений: 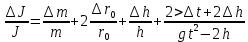 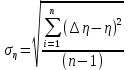 Погрешность прямых измерений: ∆t=0,001 (c); ∆h=1 (мм); ∆d=0,05 (мм); ∆r=1 (мм); ∆m= 0.5 (г). Исходные данные: m=105 г; h=46 см; d0=8,39 см; g=9,8 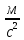 . .Таблица №1.
Таблица 2.
I.Вычисления: 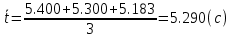 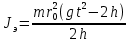 Jэ1= 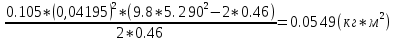 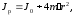 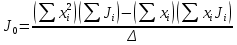 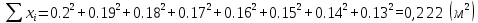 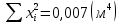 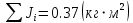 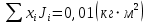 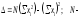 4m' = b 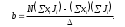 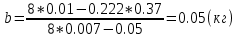 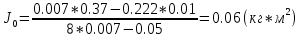 Jp1=0.06+0.05*0.2^2=0.062 (кг*м2) II. График зависимости экспериментального и теоретического значений моментов инерций Jэ и Jр от x. 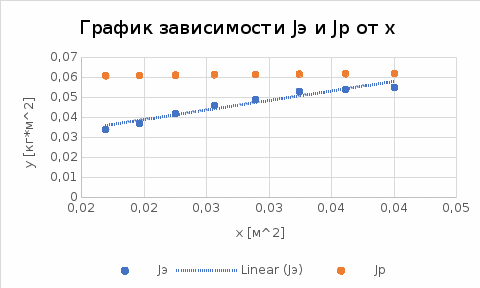 III. Дисперсия результата измерения момента инерции. 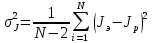 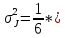 0.0015=0.00025 0.0015=0.00025 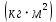 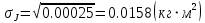 IV. Доверительный интервал. 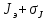 = 0.04625+0.0158=0.06205 = 0.04625+0.0158=0.06205 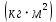 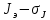 =0.04625-0.0158=0.03045 =0.04625-0.0158=0.03045 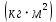 V.Расчет погрешности косвенных измерений. 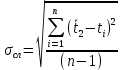 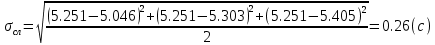 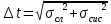 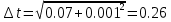 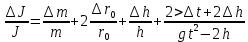 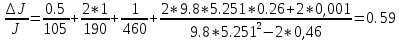 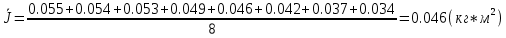 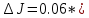 0.046=0.02 0.046=0.02
Вывод В ходе выполнения лабораторной работы были получены значения момента инерции с помощью маятника Обербека. Было установлено, что при уменьшении квадрата расстояния от центра грузов до центра масс крестовины момент инерции уменьшается прямо пропорционально времени движения. Значения момента инерции были получены двумя способами: экспериментальным и рассчитанным теоретически. Сравнение, в ходе которого было подтверждено значение среднего квадратичного отклонения, равняющееся 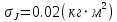 ,показало, что вычисления в рамках данных двух способов имеют значительные различия. ,показало, что вычисления в рамках данных двух способов имеют значительные различия. |