Лек5К(презКЭЛ-Ф20). Лекция 5 Сферическое движение твердого тела
 Скачать 0.81 Mb. Скачать 0.81 Mb.
|
|
ЛЕКЦИЯ 5 Сферическое движение твердого тела. Общий случай движения твердого тела. Сложное движение твердого тела Уравнения сферического движения твердого тела. Углы Эйлера. Мгновенная ось вращения. Аксоиды. Угловая скорость и угловое ускорение при сферическом движении твердого тела. Гироскоп. Общий случай движения твердого тела. Уравнения движения, число степеней свободы. Сложное движение твердого тела. Сложение вращений вокруг параллельных осей. Сложение вращений вокруг пересекающихся осей. Уравнения сферического движения твердого тела. Углы Эйлера. Мгновенная ось вращения. Аксоиды. Сферическим называется такое движение твердого тела, при котором во все время движения одна точка остается неподвижной, а остальные точки тела движутся по сферическим поверхностям, центры которых совпадают с неподвижной точкой.
Пример сферического движения твердого тела  Теорема Эйлера-Д'Аламбера: всякое элементарное движение тела, имеющего неподвижную точку, представляет собой элементарный поворот вокруг некоторой мгновенной оси вращения, проходящей через эту точку.
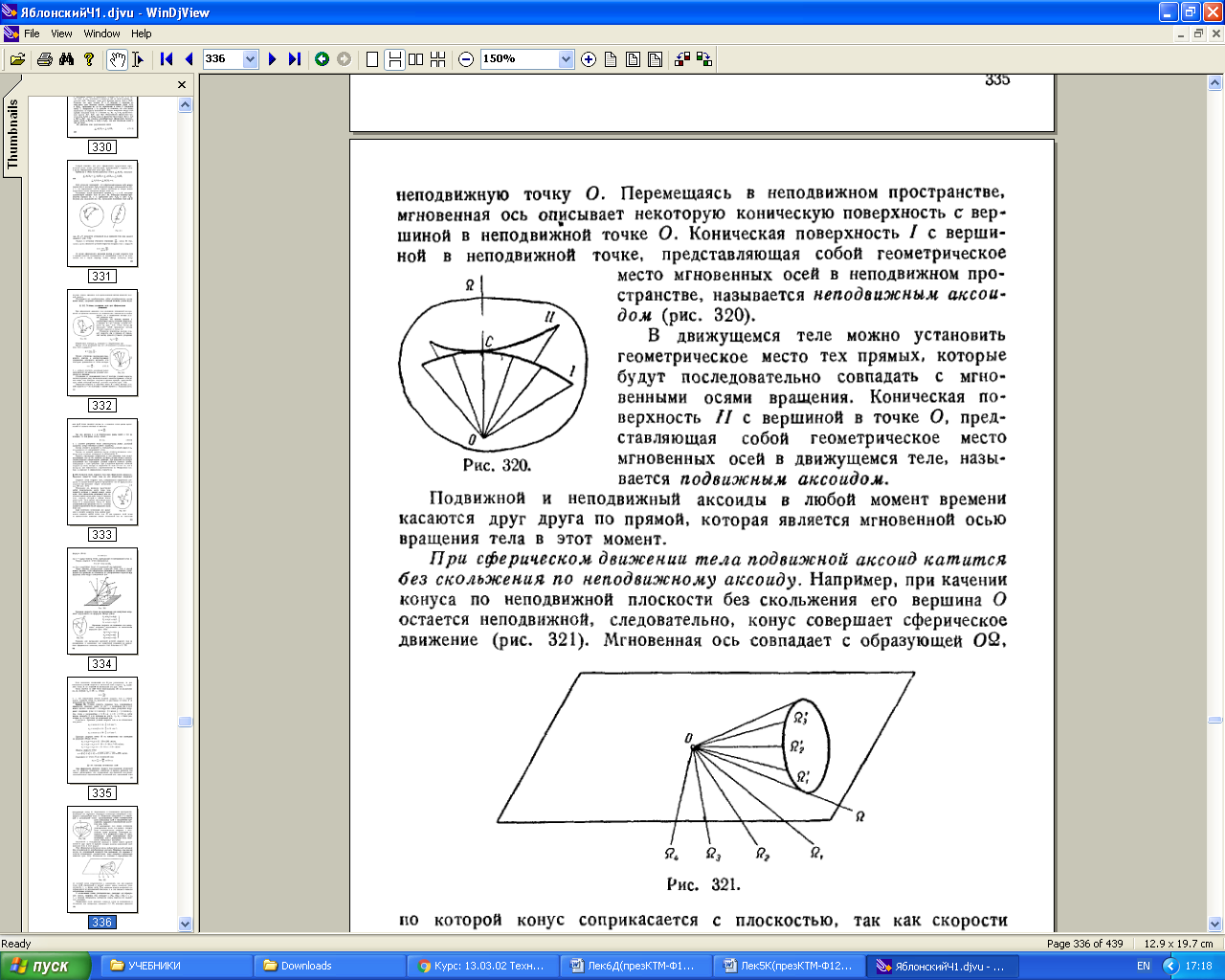
Аксоиды Положение мгновенной оси вращения не остаётся неизменным в различные моменты времени. Она занимает различные положения как в неподвижной системе отсчёта Ox1y1z1, так и в подвижной системе Оxyz неизменно связанной с телом. Коническая поверхность I с вершиной в неподвижной точке, представляющая собой геометрическое место положений мгновенных осей вращения относительно неподвижной системы отсчёта, называется неподвижным аксоидом. Коническая поверхность II с вершиной в неподвижной точке, представляющая собой геометрическое место положений мгновенных осей вращения относительно подвижной системы отсчёта называется подвижным аксоидом. При сферическом движении тела подвижный аксоид катится по неподвижному аксоиду. А линия, по которой они соприкасаются, является мгновенной осью вращения.
2. Угловая скорость и угловое ускорение при сферическом движении твердого тела.
Если обозначить через или где скорости по направлению. 3. Гироскоп — быстро вращающееся твердое тело, ось вращения которого может изменять свое направление в пространстве. По назначению гироскопические устройства подразделяются на следующие группы: Гироскопические устройства для определения угловых отклонений объекта (углы рыскания корабля или летательного аппарата, углы килевой и бортовой качки корабля, углы тангажа и крена летательного аппарата). Гироскопические устройства для определения угловых скоростей и угловых ускорений объекта. Гироскопические устройства для определения интегралов от входных величин (угловой скорости и линейных ускорений, следовательно, линейной скорости центра тяжести; угол скорости поворота). Гироскопические устройства для стабилизации объекта или прибора. Гироскопические устройства для решения навигационных задач. Модель гироскопа – карданный подвес  Первое свойство уравновешенного гироскопа с тремя степенями свободы - его ось АВ стремится устойчиво сохранять в мировом пространстве приданное ей первоначальное направление. Второе свойство гироскопа. Под действием силы F конец A оси AB будет отклоняться не в сторону действия силы, а в направлении, перпендикулярном этой силе (так как ротор вращается), следовательно, гироскоп начнет вращаться вокруг оси DE (угол ψ — прецессии). 4. Общий случай движения твердого тела. Уравнения движения. Число степеней свободы.
Движение свободного твёрдого тела рассматривается как сумма двух движений: поступательного вместе с полюсом А относительно трёх координатных осей и сферического движения относительно полюса А. Общее количество уравнений в системе (5.11) - 6 – отражает число степеней свободы свободного (не ограниченного связями) тела. Примеры свободного движения твердого тела
Сложное движение твердого тела. Сложение вращений вокруг параллельных осей. Вращения направлены в одну сторону 
Вращения направлены в разные стороны 
Пара вращений
Пара вращений эквивалентна мгновенному поступательному движению со скоростью Пример  Сложение вращений вокруг пересекающихся осей. 
|


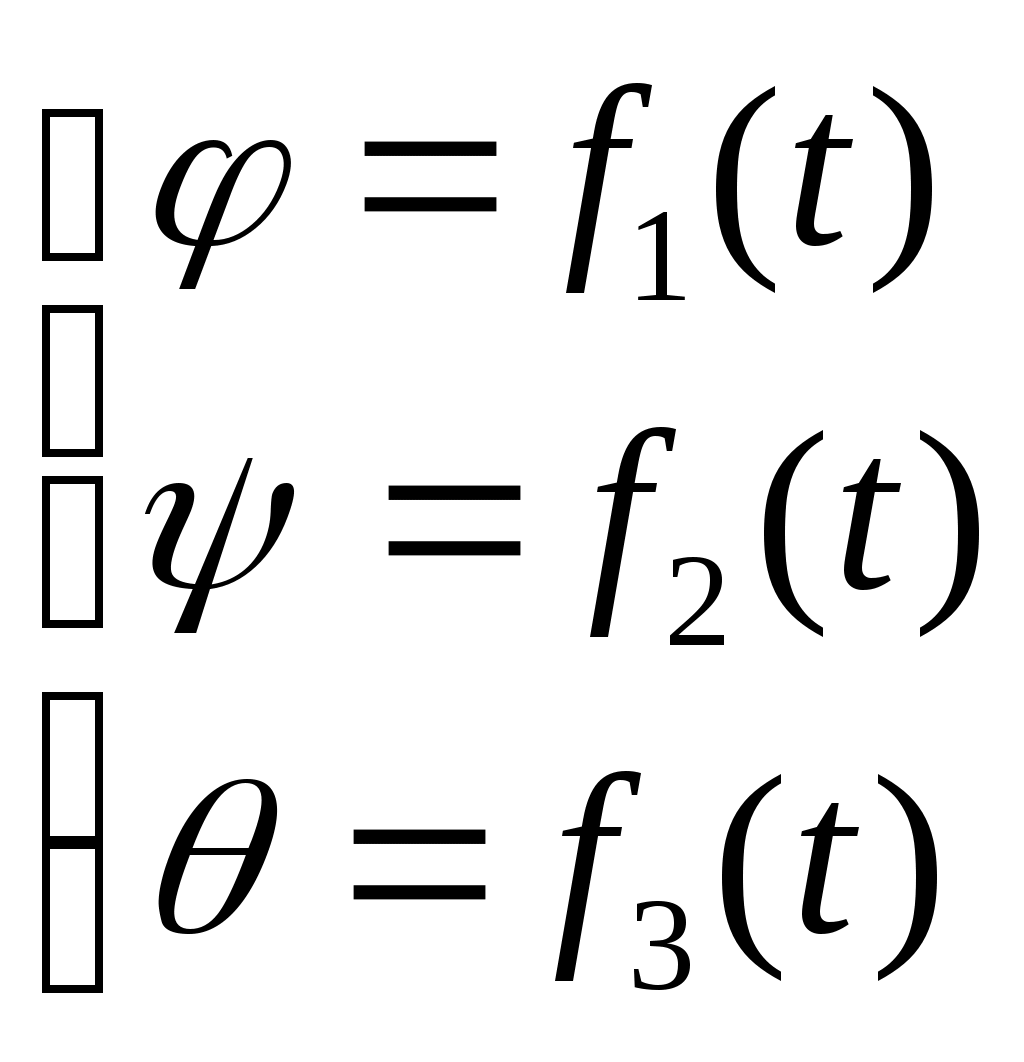


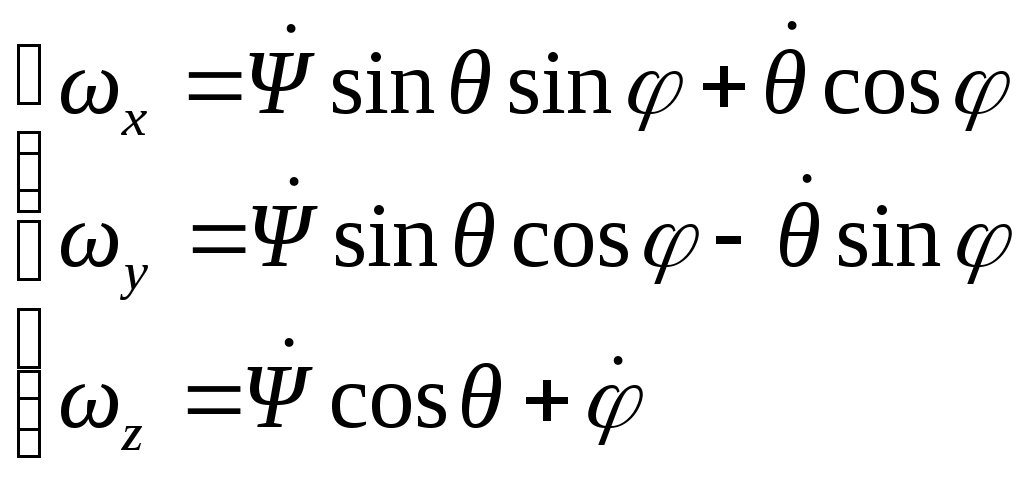 (5.2)
(5.2)
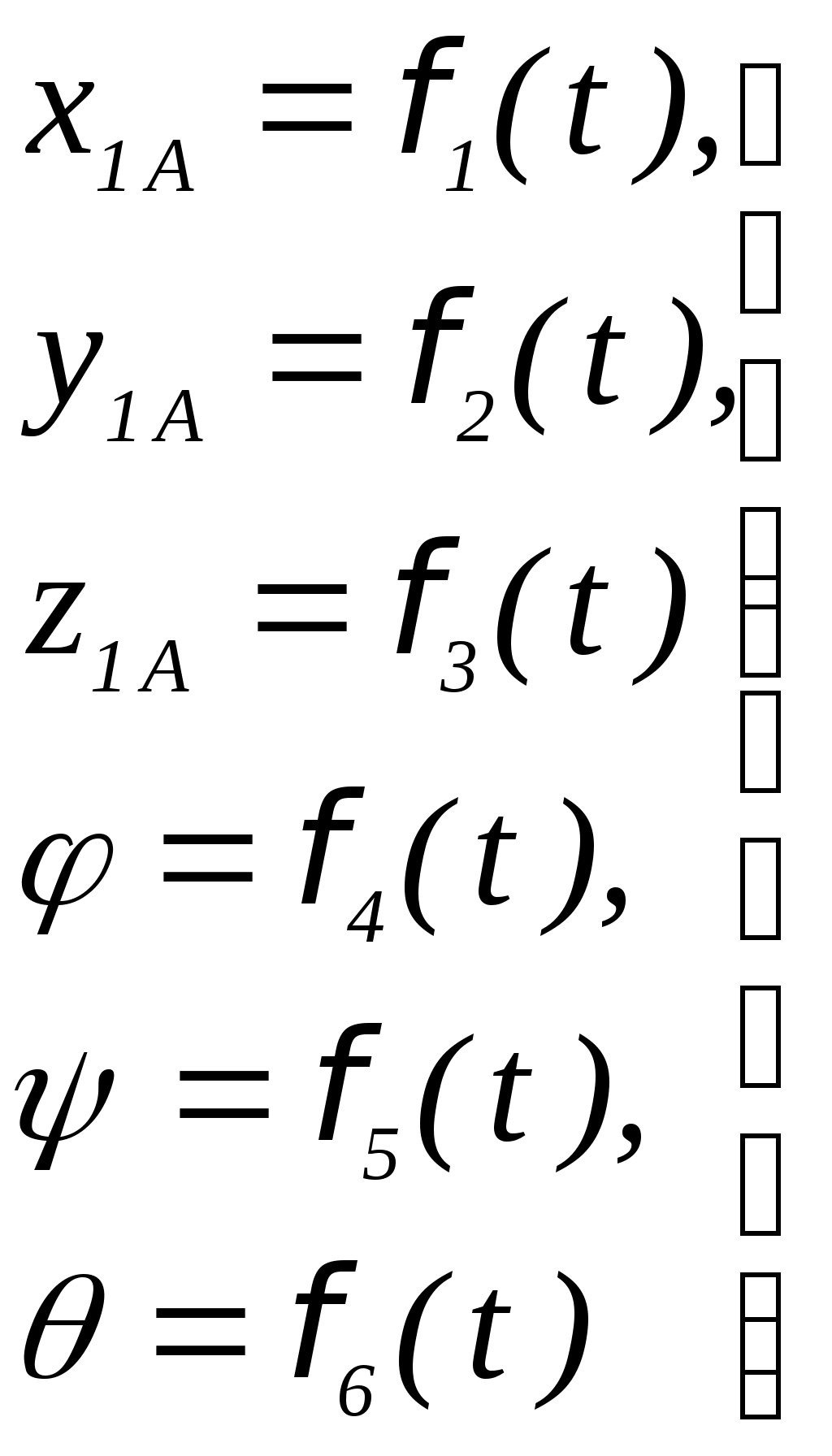 (5.11)
(5.11)

