Прикладная механика задача №1. Задача №1 прикладная механика. Решение Выполним вспомогательные действия (Рисунок 2) выберем направления осей х и у

• Название: Решение Выполним вспомогательные действия (Рисунок 2) выберем направления осей х и у
• Анкор: Прикладная механика задача №1
• Дата: 31.05.2022
• Размер: 141.03 Kb.
• Имя файла: Задача №1 прикладная механика.docx
• Тип: Решение; #560071

Задача 1

Жёсткая рама (схема1,6) закреплена в точке А с помощью шарнирно-неподвижной опоры, а в точке В с помощью шарнирно-подвижной опоры. На раму действуют равномерно распределённая нагрузка интенсивностью q, сосредоточенная сила F и пара сил с моментом М. Определить реакции опор.

Дано:

q= 60Н/м

F = 50Н

М = 40Н^.м

ℓ = 0,4м

Найти: R_А, Х_А, У_А.

.

Рисунок 1. Расчетная схема

Решение:

Выполним вспомогательные действия (Рисунок 2)

- выберем направления осей х и у;

- для вектора силы F покажем его углы наклона не только от вертикальной линии, но и от горизонтали (90⁰-60⁰=30⁰);

-равномерно распределённую нагрузку интенсивности q заменим равнодействующей Q (равнодействующая равномерно распределённой нагрузки приложена посередине её участка и равна произведению её интенсивности на длину участка; в данном случае Q= q2L, или Q=60кН/м^.2 ^.0,4м=48кН );

шарнирно-неподвижную опору А заменим двумя составляющими реакции Х_А и У_А ), которые параллельны осям х и у и направлены в те же стороны, что и оси;

- шарнирно-подвижную опору В заменим реакцией R_B: она перпендикулярна плоскости, по которой катается опора и направлена от рамы.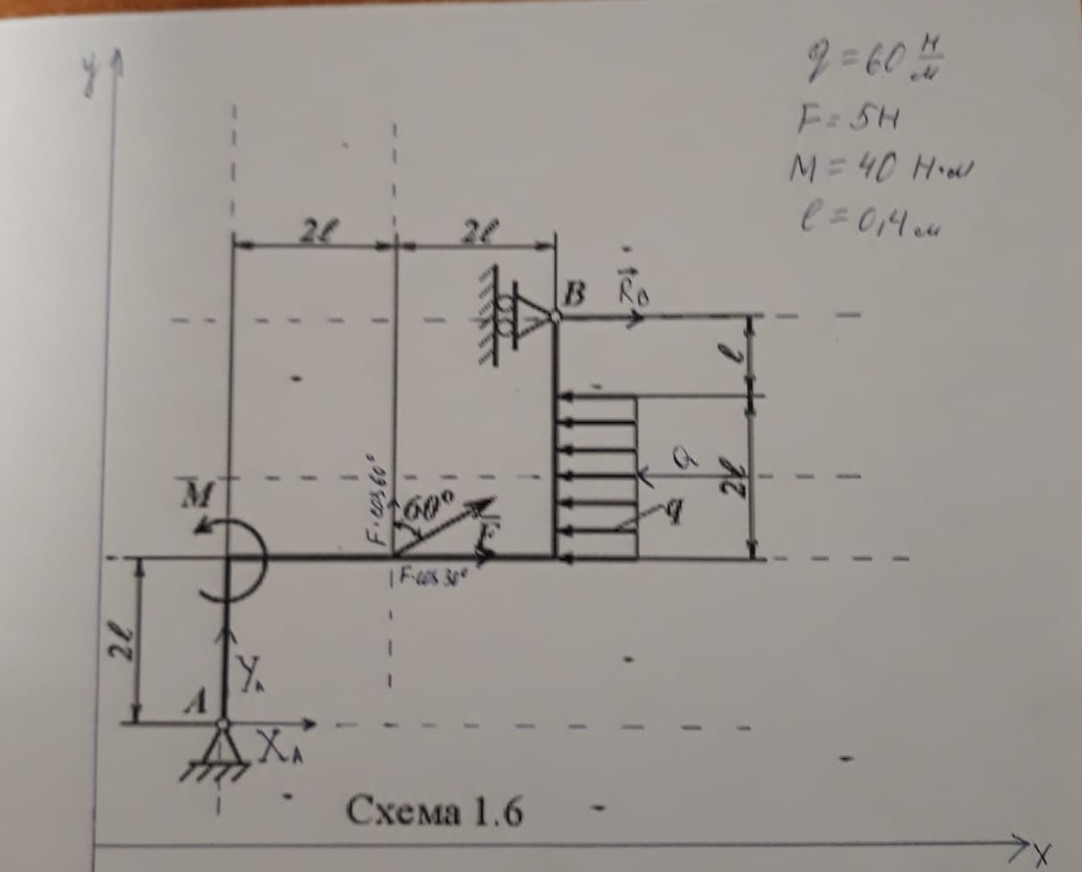



Рисунок 2. Схема нагружения рамы, эквивалентная заданной

Для полученной плоской системы сил (рисунок 2) составляем уравнения равновесия. ( Правила их составления :

Проекция силы на ось равна произведению величины силы на косинус угла между этой силой и этой осью.

Правило знака: проекция силы на ось считается положительной, если направление составляющей силы (параллельной оси) совпадает с направлением этой оси;

проекция силы на ось будет отрицательной, если направление составляющей силы (параллельной оси) противоположно направлению этой оси)
Сумма проекций на ось х всех действующих сил равна нулю

т. е. У_А + F ^. cos 60⁰ = 0; (1)

У_А = - F ^. cos 60⁰;

У_А = -5 ^.0,5 = -2,5(кН).

Сумма проекций на ось у всех действующих сил равна нулю

т. е. Х_А - Q + F ^. cos30⁰ + R_В = 0; (2)

отсюда Х_А = Q - F ^. cos30⁰ - R_В

Поскольку в уравнении (2) имеются две неизвестны величины (Х_А и R_В), оставляем его пока нерешённым.

Сумма моментов относительно точки А от всей действующей нагрузки равна нулю;

Применяя правила вычисления моментов, а для нахождения момента силы теорему Вариньона

(Момент сил относительно какой –либо точки О вычисляется по формуле M=F· h, где h плечо силы F относительно точки О.

Плечо силы относительно точки О это кратчайшее расстояние (т.е. длина перпендикуляра) от то О до линии действия силы;

знак «плюс» берут, если сила F стремится вращать тело вокруг

заданной точки О против хода часовой стрелки;

знак «минус» берут, если сила F стремится вращать тело

вокруг заданной точки О по ходу часовой стрелки.

Момент силы относительно точки равен нулю в единственном случае, когда плечо силы равно нулю, т. е. когда линия действия силы проходит через эту точку)

получаем:

+Q ^. 3ℓ + M + Fcos60^{0 .} 2ℓ - Fcos30^{0 .} 2ℓ - R_В ^. 5ℓ = 0; (3)

R_В ^. 5ℓ = Q ^. 3ℓ + M + Fcos60^{0 .} 2ℓ - Fcos30^{0 .} 2ℓ ;

R_В =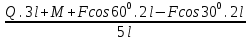

В результате R_B = 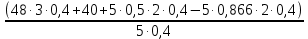= = = 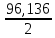48,068 (кН)

R_B =48,068 кН

Теперь в уравнении (2) осталась только одна неизвестная,

Х_А = Q - F ^. cos30⁰ - R_В, подставив значение R_B получим:

Х_А = 48 - 5·0,866 - 48,068 = 48 - 4,33 - 48,068 = - 4,396 (кН)

Ответ X_А = - 4,398 кН ; Y_А = - 2,5кН; R_В = 48,068 кН.

Знак «минус» указывает на то, что действительное направление силы Х_А и У_А противоположно указанному на рисунке 2.

Задача решена.

Выполним проверку правильности нахождения опорных реакций. Для этого нужно проверить равенство нулю суммы моментов всей нагрузки относительно точки В: 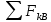=0

Применяя правила вычисления моментов , определив плечи как длины перпендикуляров, опущенных из точки В на линии действия сил (рисунок 2) получаем

-Q·2ℓ + Fcos30⁰·3ℓ- Fcos60⁰ ·2ℓ + M -Y_A·4ℓ + Х_A·5ℓ = 0;

Подставив значения получим

-48 ·0,8 +5·0,866·3·0,4 – 5·0,5·2·0,4 + 2,5·4·0,4 – 4,398·5·0,4= -38,4 + 5,169 – 2 + 40 + 4 -8,796 = -49,196 +49,166 = 0 .

Получили что сумма моментов всей нагрузки относительно точки В=0, следовательно опорные реакции найдены верно.