Лаба. Простейшие движения твердого тела
 Скачать 260.35 Kb. Скачать 260.35 Kb.
|
|
ЛЕКЦИЯ 2 ПРОСТЕЙШИЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА Поступательное движение Поступательным называется такое движение твёрдого тела, при котором любая прямая, проведённая в этом теле, перемещается, оставаясь параллельной самой себе. При поступательном движении тела траектории его точек могут быть любыми кривыми линями. Теорема. При поступательном движении все точки тела описывают одинаковые (при наложении совпадающие) траектории и имеют в каждый момент времени одинаковые по модулю и направлению скорости и ускорения.  Рассмотрим твёрдое тело, совершающее поступательное движение относительно системы осей Оxyz. Возьмём в теле две произвольные точки А и В, положение которых в момент времени t определяется радиус-векторами Рассмотрим твёрдое тело, совершающее поступательное движение относительно системы осей Оxyz. Возьмём в теле две произвольные точки А и В, положение которых в момент времени t определяется радиус-векторами 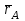 и и 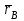 . Проведём вектор . Проведём вектор  соединяющий эти точки, тогда соединяющий эти точки, тогда  . При этом длинна . При этом длинна  , как расстояние между точками твёрдого тела, а направление остаётся неизменным, так как тело движется поступательно. Вектор , как расстояние между точками твёрдого тела, а направление остаётся неизменным, так как тело движется поступательно. Вектор  во всё время движения остаётся постоянным по величине и направлению. Вследствие этого, траектории точки В (вектор во всё время движения остаётся постоянным по величине и направлению. Вследствие этого, траектории точки В (вектор 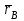 ) получается из траектории точки А (конец вектора ) получается из траектории точки А (конец вектора 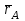 ) параллельным смещением всех её точек на постоянный вектор ) параллельным смещением всех её точек на постоянный вектор  . Следственно, траектории всех точек А и В будут действительно одинаковыми (при наложении совпадающие) кривыми. . Следственно, траектории всех точек А и В будут действительно одинаковыми (при наложении совпадающие) кривыми. Для нахождения скоростей точек А и В продифференцируем обе части равенства по t 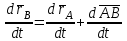 , , но  , так как , так как  ; ; 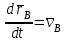 , ,  ; ;отсюда 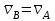 , ,т.е. скорости точек А и В тела любой момент времени одинаковы по величине и направлению. Беря от обеих частей полученного равенства производные по времени, найдём  , , 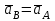 , ,следственно, ускорение точек А и В тела в любой момент времени тоже одинаковы по модулю и направлению. Так как точки А и В были выбраны произвольно, то из полученных результатов следует, что у всех точек тела их траектории, а так же скорости и ускорения в любой момент времени будут одинаковы. Из теоремы следует, что поступательное движение твёрдого тела вполне определяется движением какой-нибудь одной его точки (как правило, за такую точку принимают центр тяжести тела). Следственно, изучение поступательного движения тела сводится к задаче «кинематики точки», уже изученной. При поступательном движении общую для всех точек тела скорость  называют скоростью поступательного движения тела, а ускорение называют скоростью поступательного движения тела, а ускорение  — ускорением поступательного движения. Векторы — ускорением поступательного движения. Векторы  и и  можно изображать приложенными в любой точке тела. можно изображать приложенными в любой точке тела. Понятие о скорости и ускорении тела имеют смысл только при поступательном движении. Вращательное движение твёрдого телаВращательным называется такое движение твёрдого тела, при котором какие-нибудь две точки, принадлежащие телу (или неизменно с ним связанные), остаются во всё время движения неподвижными. 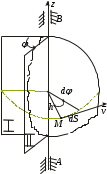 Проходящая через неподвижные точки А и В прямая АВ называется осью вращения. Так как рассматривается твёрдое тело, то все точки принадлежащие оси вращения будут неподвижны, а остальные будут описывать окружности, центры которых лежат на этой оси. Проходящая через неподвижные точки А и В прямая АВ называется осью вращения. Так как рассматривается твёрдое тело, то все точки принадлежащие оси вращения будут неподвижны, а остальные будут описывать окружности, центры которых лежат на этой оси. Для определения положения тела проведём через ось вращения АВ две полуплоскости: I — неподвижную, II — вращающуюся вместе с телом. Тогда положение тела в любой момент времени будет однозначно определяться углом 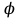 между этими плоскостями, который называется углом поворота тела. между этими плоскостями, который называется углом поворота тела. Считаем 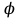 >0, если он отложен от плоскости I против часовой; >0, если он отложен от плоскости I против часовой; 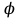 <0, если – по часовой (для наблюдателя, смотрящего с положительного конца оси z). <0, если – по часовой (для наблюдателя, смотрящего с положительного конца оси z). Что бы знать положение тела в любой момент времени, надо знать зависимость 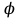 от времени, т.е. от времени, т.е.  , ,закон вращательного движения твёрдого тела. Основными кинематическими характеристиками вращательного движения является его угловая скорость  и угловое ускорение и угловое ускорение  . . Если за промежуток времени 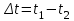 тело совершает поворот на угол тело совершает поворот на угол  , то средняя угловая скорость тела за этот промежуток времени будет численно равна , то средняя угловая скорость тела за этот промежуток времени будет численно равна  , при , при  , , 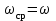 ; ;  ; ;угловая скорость в данный момент времени численно равна первой производной от угла поворота по времени. Угловую скорость можно выразить в виде вектора  , который направлен вдоль оси вращения тела в ту сторону, откуда вращение видно происходящим против хода часовой стрелки. , который направлен вдоль оси вращения тела в ту сторону, откуда вращение видно происходящим против хода часовой стрелки. Угловое ускорение характеризует изменение угловой скорости тела с течением времени. Если за промежуток времени 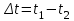 угловая скорость тела изменяется на величину угловая скорость тела изменяется на величину  , то среднее угловое ускорение тела за этот промежуток времени будет численно равна: , то среднее угловое ускорение тела за этот промежуток времени будет численно равна:  , при , при  , , 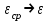 ; ; ; ;угловое ускорение тела в данный момент времени численно равна первой производной от угловой скорости или второй производной от угла поворота по времени. Если модуль угловой скорости со временем возрастает, вращение называется ускоренным, а если убывает — замедленным. Угловое ускорение тела так же можно выразить в виде вектора  , направленного вдоль оси вращения. , направленного вдоль оси вращения. Когда тело вращается ускоренно, векторы  и и  по направлению совпадают, когда замедленно — по направлению совпадают, когда замедленно —  и и  направлены противоположно. направлены противоположно.Равномерное и равнопеременное вращение твёрдого тела1. Если угловая скорость тела остаётся во всё время движения постоянной ( 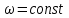 ), то вращение тела называется равномерным. ), то вращение тела называется равномерным. Так как 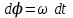 , ,  ; ;но – const, и полагая, что при 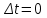 , , 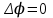 , начало движения, то тогда , начало движения, то тогда  , или , или 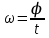 . .В технике скорость равномерного вращения часто определяют числом оборотов в минуту, обозначая эту величину n об/мин. При одном обороте тело поворачивается на угол  , а при n оборотах на , а при n оборотах на  , этот поворот делается за время t = 1 мин = 60 c, тогда , этот поворот делается за время t = 1 мин = 60 c, тогда  . .2. Если угловое ускорение тела во всё время движения остаётся постоянным ( 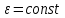 ), то вращение называется равнопеременным. ), то вращение называется равнопеременным. Считая, что в начальный момент при 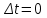 , угол , угол 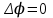 , а угловая скорость , а угловая скорость  ( ( — начальная угловая скорость), зная что — начальная угловая скорость), зная что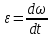 , ,  , ,  ; ;  , ,далее 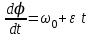 , ,  ; ;проинтегрировав, найдём закон равнопеременного вращения 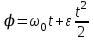 . .Если  и и  имеют одинаковые знаки, то вращение будет равноускоренным, разные — равнозамедленным. имеют одинаковые знаки, то вращение будет равноускоренным, разные — равнозамедленным.Скорости и ускорения точек вращающегося телаРассмотрим какую-нибудь точку М твёрдого тела, находящегося на расстоянии h от оси вращения АВ. При вращении тела точка М будет описывать окружность радиуса h, плоскость которой перпендикулярна к оси вращения, а центр С лежит на самой оси. Если за время dtпроисходит элементарный поворот тела на угол  , то точка М при этом совершает вдоль своей траектории элементарное перемещение , то точка М при этом совершает вдоль своей траектории элементарное перемещение 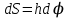 . Тогда скорость точки будет равна отношению dS к dt, т.е. . Тогда скорость точки будет равна отношению dS к dt, т.е. 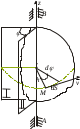  , ,  ; ;скорость  называется линейной или окружной скоростью точки М. называется линейной или окружной скоростью точки М. Линейная скорость точки вращающегося твёрдого тела численно равна произведению угловой скорости тела на расстояние от этой точки до оси вращения. Направлена линейная скорость по касательной к описываемой точкой М окружности. Так как для всех точек тела  имеет в данный момент одно и тоже значение, то линейные скорости точек вращающегося тела пропорциональны их расстояниям от оси вращения. имеет в данный момент одно и тоже значение, то линейные скорости точек вращающегося тела пропорциональны их расстояниям от оси вращения. Ускорение точек вращающегося телаТак как все точки, принадлежащие вращающемуся телу, описывают окружности т.е. имеют криволинейную траекторию, то их ускорения складываются из нормального (центростремительного) и тангенциального (вращательного). Выразим их значения через угловые параметры тела  , но v = h, авр. = а = , но v = h, авр. = а =  ; ;  , где = h, ац= , где = h, ац=  = h2. = h2. Вращательное ускорение а направленно по касательной (в сторону движения, если тело вращается ускоренно, или в обратную сторону, если тело вращается замедленно); центростремительное ускорение ац всегда направленно по радиусу h к оси вращения. Полное ускорение точки М равно 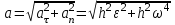 , , 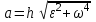 . .Отклонение вектора полного ускорения от радиуса окружности определяется углом 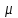 , который определяется по формуле , который определяется по формуле . .Преобразование простейших движенийПод преобразованием простейших движений следует понимать: 1. Преобразование вращательного движения в поступательное (и наоборот); 2. Преобразование вращения вокруг одной неподвижной оси во вращение вокруг другой неподвижной оси; 3.Преобразование одного поступательного движения в другое поступательное движение. При решении задач о движении механизмов, преобразующих простейшие движения, следует пользоваться совместно формулами кинематики точки и кинематики твёрдого тела, вращающегося вокруг неподвижной оси.   Преобразования вращения одного твёрдого тела вокруг неподвижной оси во вращение второго твёрдого тела вокруг другой неподвижной оси осуществляется посредством зубчатого или фрикционного зацепления двух колёс или при помощи ременной передачи. 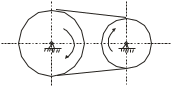  При внутреннем зацеплении и простой ременной передаче направления вращения обоих колёс совпадают. При внешнем зацеплении и скрещивающейся ременной передаче направление вращения колёс противоположны. Передача движения происходит за счёт равенства линейных скоростей в точке контакта (или на ободе шкивов ременной передачи). Основной кинематической характеристикой передачи движения является передаточное отношение u, которое прямо пропорционально отношению угловых скоростей колёс или обратно пропорционально числам зубьев (радиусам) колёс u = 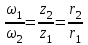 ; ;где 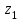 , , 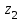 — числа зубьев колёс, — числа зубьев колёс, 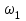 , ,  — модули угловых скоростей. — модули угловых скоростей. Если на одном валу неподвижно закреплено несколько колёс, то их угловые скорости равны. Вопросы для самоконтроля Какое движение твердого тела называется поступательным? Основная теорема поступательного движения твердого тела. Какое движение твердого тела называется вращательным? По каким траекториям двигаются точки твердого тела при вращательном движении? Как определить угловые скорость и ускорение твердого тела? Как определить линейную скорость точки твердого тела при его вращательном движении и как она направлена? Как определить ускорение точки твердого тела, вращающегося вокруг неподвижной оси? Как направлены и чему равны его составляющие? Какие виды передачи движения существуют? Что является характеристикой передачи движения? |
