Лабораторная работа № 6 Моделирование фу. Лабораторная работа 6 Тема работы Моделирование функционирования распознавателя для ll (1) грамматик
 Скачать 0.58 Mb.
|
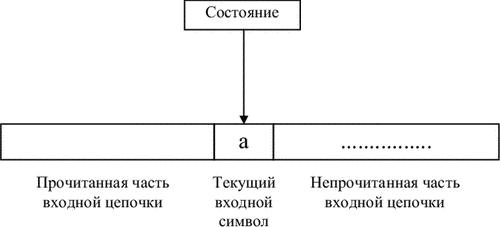
Постановка задачи к лабораторной работе № 6Разработать программное средство, автоматизирующее процесс разбора цепочек для LL(1)-грамматик. Программное средство должно выполнять сле- дующие функции: реализация ввода произвольной КС-грамматики; построение множеств FIRST(1, A) и FOLLOW(1, A) для каждого нетер- минального символа грамматики; проверка необходимого и достаточного условия LL(1) для введенной КС-грамматики; моделирование функционирования распознавателя для LL(1)- грамматик. Составить набор контрольных примеров для случаев: а) введенная КС-грамматика не является LL(1)-грамматикой; б) исходная КС-грамматика является LL(1)-грамматикой, но входная строка не принадлежит языку грамматики; в) заданная КС-грамматика является LL(1)-грамматикой и введенная строка принадлежит языку грамматики. 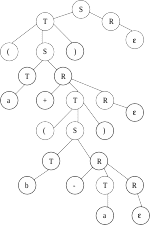 Разбор цепочек показать с помощью таблицы, строки вывода и дерева вывода. Вариантами индивидуальных заданий к лабораторной работе № 6 яв- ляются выходные данные лабораторной работы № 4. Рисунок 6.1 – Дерево вывода для цепочки (a+(b-a)) в грамматике G РЕШЕНИЕ: При выполнении лабораторной работы № 6 - выявим понятие «LL(k) - грамматики», необходимые и достаточные условия LL(k) –грамматики; сформируем умения и навыки построения множеств FIRST(k, ) и FOLLOW(k, ), распознавателя для LL(1)-грамматик. 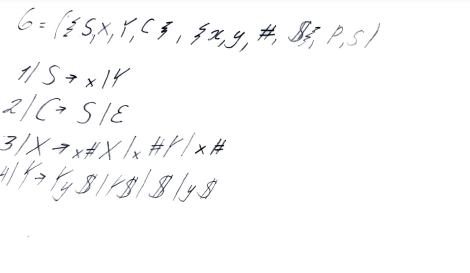 Рис 1.1 Алгоритм работы Получение практических навыков построения моделей конечных распознавателей. Недетерминированный конечный автомат (НКА) - это пятерка M = (Q, T, D, q0, F), где Q - конечное множество состояний; T - конечное множество допустимых входных символов (входной алфавит); D - функция переходов (отображающая множество Q(T  {e}) во множество подмножеств множества Q), определяющая поведение управляющего устройства; q0  Q - начальное состояние управляющего устройства; F  Q - множество заключительных состояний.Работа конечного автомата представляет собой некоторую последовательность шагов, или тактов. Такт определяется текущим состоянием управляющего устройства и входным символом, обозреваемым в данный момент входной головкой. Сам шаг состоит из изменения состояния и, возможно, сдвига входной головки на одну ячейку вправо (рис. 9.2).
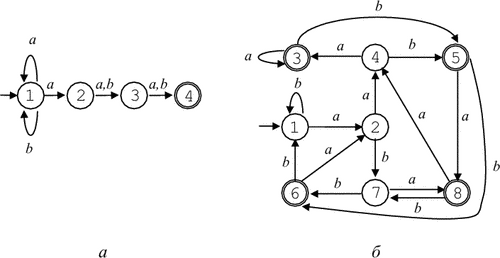
Недетерминизм автомата заключается в том, что, во-первых, находясь в некотором состоянии и обозревая текущий символ, автомат может перейти в одно из, вообще говоря, нескольких возможных состояний, и во-вторых, автомат может делать переходы по e. Пусть M = (Q, T, D, q0, F) - НКА. Конфигурацией автомата M называется пара (q, w) QT*, где q - текущее состояние управляющего устройства, а w - цепочка символов на входной ленте, состоящая из символа под головкой и всех символов справа от него. Конфигурация (q0, w) называется начальной, а конфигурация (q, e), где q F - заключительной (или допускающей). Пусть M = (Q, T, D, q0, F) - НКА. Тактом автомата M называется бинарное отношение  , определенное на конфигурациях M следующим образом: если p D(q, a), где a T {e}, то (q, aw) (p, w) для всех w T*. Будем обозначать символом + ( *) транзитивное (рефлексивно- транзитивное) замыкание отношения . Говорят, что автомат M допускает цепочку w, если (q0, w) *(q, e) для некоторого q F. Языком, допускаемым (распознаваемым, определяемым) автоматом M, (обозначается L(M)), называется множество входных цепочек, допускаемых автоматом M. Т.е.  Важным частным случаем недетерминированного конечного автомата является детерминированный конечный автомат, который на каждом такте работы имеет возможность перейти не более чем в одно состояние и не может делать переходы по e. Пусть M = (Q, T, D, q0, F) - НКА. Будем называть M детерминированным конечным автоматом (ДКА), если выполнены следующие два условия: D(q, e) =  для любого q Q, и D(q, a) содержит не более одного элемента для любых q Q и a T.Так как функция переходов ДКА содержит не более одного элемента для любой пары аргументов, для ДКА мы будем пользоваться записью D(q, a) = p вместо D(q, a) = {p}. Конечный автомат может быть изображен графически в виде диаграммы, представляющей собой ориентированный граф, в котором каждому состоянию соответствует вершина, а дуга, помеченная символом a T {e}, соединяет две вершины p и q, если p D(q, a). На диаграмме выделяются начальное и заключительные состояния (в примерах ниже, соответственно, входящей стрелкой и двойным контуром). Пример 9.1. Пусть L = L(r), где r = (a|b)*a(a|b)(a|b). Недетерминированный конечный автомат M, допускающий язык L:
где функция переходов D определяется так:
Диаграмма автомата приведена на рис. 9.2, а. Детерминированный конечный автомат M, допускающий язык L:
где функция переходов D определяется так:
Диаграмма автомата приведена на рис. 9.2, б.
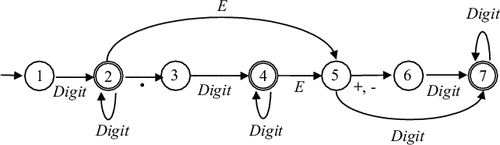
Пример 9.2. Диаграмма ДКА, допускающего множество чисел в десятичной записи, приведена на рис. 9.4.
Пример 9.3. Анализ цепочек. При анализе цепочки w = ababa автомат из примера 9.2, а, может сделать следующую последовательность тактов: (1, ababa)  (1, baba) (1, aba) (2, ba) (3, a) (4, e). Состояние 4 является заключительным, следовательно, цепочка w допускается этим автоматом. При анализе цепочки w = ababab автомат из примера 9.2, б, должен сделать следующую последовательность тактов: (1, ababab) (2, babab) (7, abab) (8, bab) (7, ab) (8, b) (7, e). Так как состояние 7 не является заключительным, цепочка w не допускается этим автоматом. Конечный распознаватель – это модель устройства с конечным числом состояний, которое отличает правильно образованные, или «допустимые» цепочки, от «недопустимых». Примером задачи распознавания может служить проверка нечетности числа единиц в произвольной цепочке, состоящей из нулей и единиц. Соответствующий конечный автомат будет допускать все цепочки, содержащие нечетное число единиц, и отвергать все цепочки с четным их числом. Назовем его «контролером нечетности». На вход конечного автомата подается цепочка символов из конечного множества, называемого входным алфавитом автомата, и представляющего собой совокупность символов, для работы с которыми он предназначен. Как допускаемые, так и отвергаемые автоматом цепочки, состоят только из символов входного алфавита. Символы, не принадлежащие входному алфавиту, нельзя подавать на вход автомата. Входной алфавит контроллера нечетности состоит из двух символов: «0» и «1». В каждый момент времени конечный автомат имеет дело лишь с одним входным символом, а информацию о предыдущих символах входной цепочки сохраняет с помощью конечного множества состояний. Согласно этому представлению, автомат помнит о прочитанных ранее символах только то, что при их обработке он перешел в некоторое состояние, которое и является памятью автомата о прошлом. Контролер нечетности будет построен так, чтобы он умел запоминать, четное или нечетное число единиц ему встретилось при чтении входной цепочки. Исходя из этого, множество состояний конструируемого автомата содержит два состояния: «чет» и «нечет». Одно из этих состояний должно быть выбрано в качестве начального, предполагается, что автомат начнет работу в этом состоянии. Начальным состоянием контролера нечетности будет «чет», так как на первом шаге число прочитанных единиц равно нулю, а нуль – четное число. При чтении очередного символа состояние автомата меняется, причем новое его состояние зависит только от входного символа и текущего состояния. Такое изменение состояния называется переходом. При переходе может оказаться, что новое состояние совпадает со старым. Работу автомата можно описать математически с помощью функции переходов, которая по текущему состоянию  и текущему входному символу  дает новое состояние автомата  . Символически эта зависимость описывается так:  .Учитывая, что состояния «чет» и «нечет» означают соответственно, четное и нечетное количество прочитанных единиц, определим функцию переходов контролера нечетности следующим образом: 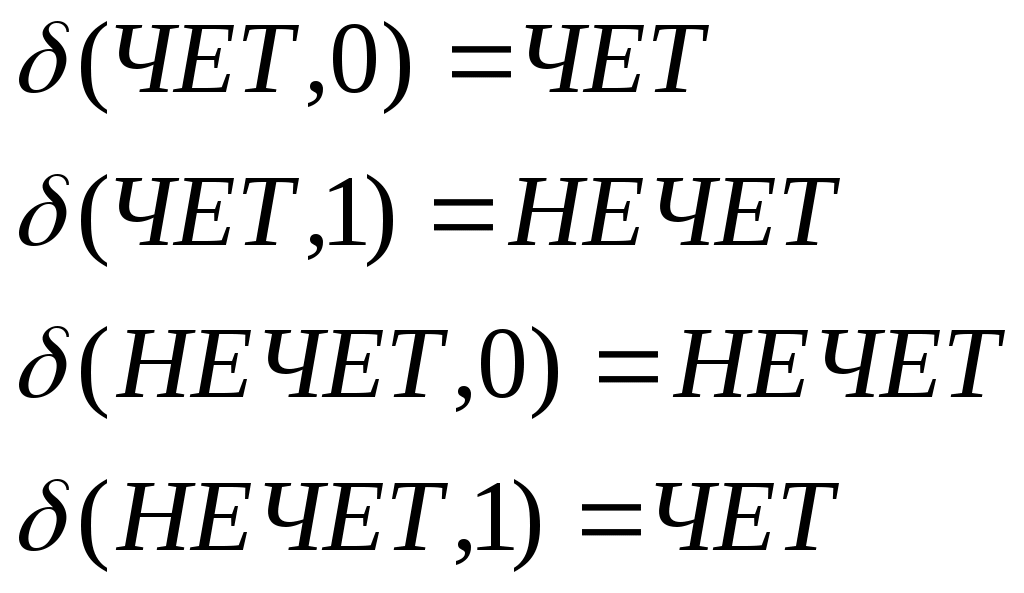 Эта функция переходов отражает тот факт, что четность меняется тогда и только тогда, когда на входе читается единица. Некоторые состояния автомата выбираются в качестве допускающих, или заключительных. Если автомат, начав работу в начальном состоянии, при прочтении всей цепочки переходит в одно из допускающих состояний, то говорят, что эта цепочка допускается автоматом. Если последнее состояние автомата не является допускающим, то говорят, что автомат отвергает цепочку. Контролер нечетности имеет единственное допускающее состояние – «НЕЧЕТ». Переход автомата из состояния в состояние  при чтении входного символа Х будем наглядно изображать так:  . Например, для контролера нечетности можно написать: . Аналогичным образом можно изобразить последовательность переходов: Эта запись показывает, как автомат в состоянии «ЧЕТ» применяется к цепочке «1101». Входную цепочку «101» автомат отвергает, т.к. она переводит его из начального состояния в состояние, не являющееся допускающим. Символически это изображается так:  .Контролер нечетности распознает множество цепочек, состоящих из нулей и единиц, и содержащее нечетное число единиц. Множество всех цепочек, распознаваемых конечным автоматом, называется регулярным множеством. Один из удобных способов представления конечных автоматов – это таблица переходов. Для контролера нечетности такая таблица выглядит следующим образом:
Информация в таблице переходов размещается в соответствии со следующими соглашениями: Столбцы помечены входными символами; Строки помечены символами состояний; Элементами таблицы являются символы новых состояний, соответствующих входным символам столбцов и состояниям строк; Первая строка помечена символом начального состояния; Строки, соответствующие допускающим (заключительным) состояниям, помечены справа единицами, а строки, соответствующие отвергающим состояниям, помечены справа нулями. Таким образом, приведенная таблица переходов задает конечный автомат, у которого: Входное множество ={0,1}; Множество состояний ={ЧЕТ, НЕЧЕТ}; Функции переходов: 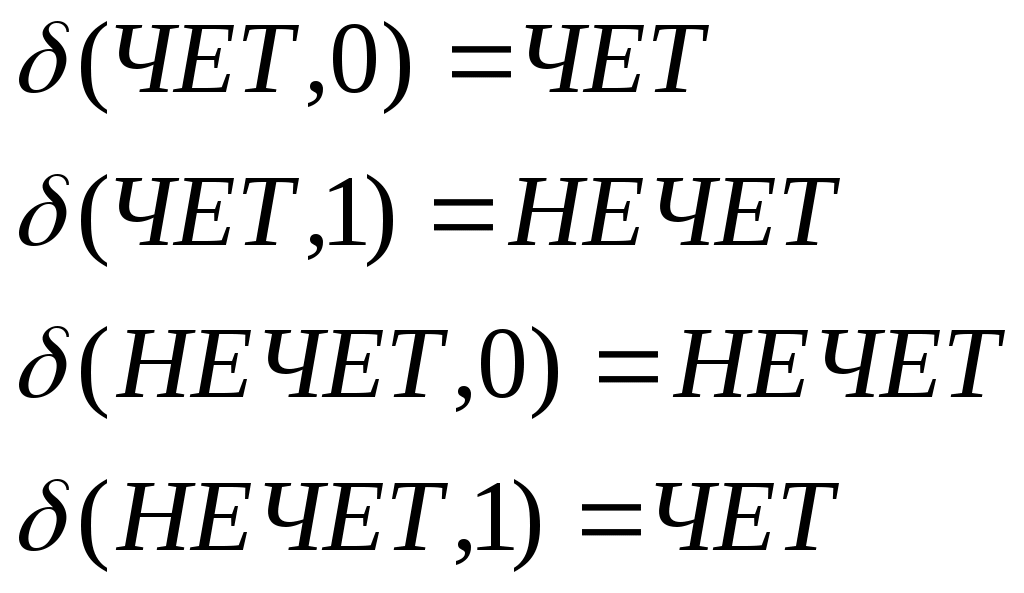Начальное состояние = {ЧЕТ}; Допускающие состояния = {НЕЧЕТ}. Простейшая программная реализация КА – контроллера нечетности: #include "stdafx.h" #include "iostream.h" #include "stdio.h" #include "conio.h" int per (int tsost, char tsymb) {int slsost; switch (tsymb) { case '0': if (tsost==0) slsost=0; else slsost=1; case '1': if (tsost==1) slsost=0; else slsost=1;} return slsost; }; int main() { int i,kol,tsost,slsost; char ch, inpstr[80] ; printf("ENTER STRING "); i=0; while ((ch=getch()) !=13 && i<80) //ïîêà íå íàæàòà êëàâèøà {putch(ch); inpstr[i++]=ch;} inpstr[i]='\0'; kol=i-1; printf("\n input string:"); printf(inpstr); tsost=0; for (i=0;i<=kol;i=i+1) { slsost=per(tsost,inpstr[i]); tsost=slsost; }; switch (slsost) { case 0:cout<<"\n STRING is WRONG "; case 1:cout<<"\n STRING is RIGHT ";}; return 0; |
