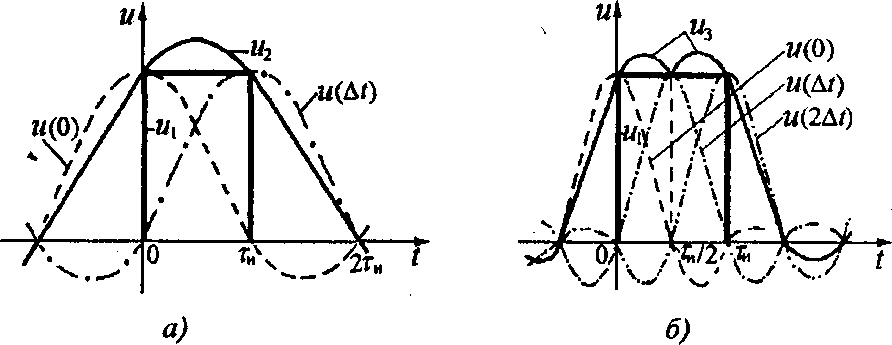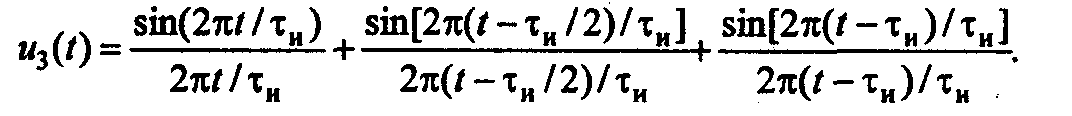ЛАБОРАТОРНАЯ РАБОТА №7
Представление случайного сигнала рядом Котельникова.
ЗАДАНИЕ
Представить рядом Котельникова случайный сигнал X(t) , используя первые 7 значений случайного сигнала (по данным Вашего варианта). С этой целью рассмотреть случаи  =1с и =1с и  =2с. =2с.
В качестве образца воспользуйтесь приведённым ниже примером.
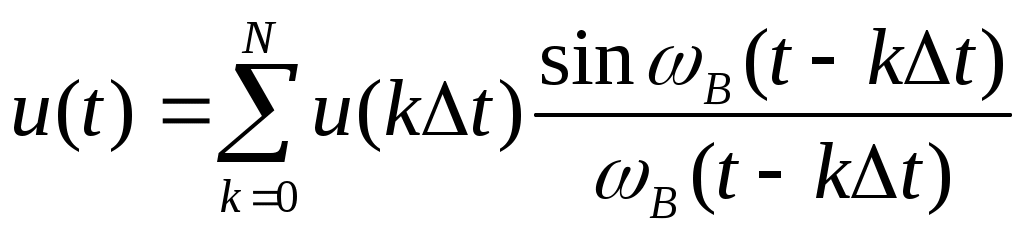 , (3.1) , (3.1)
где k =0, 1, 2, 3. 4, …, N – целые числа,
 B – верхняя граничная частота. B – верхняя граничная частота.
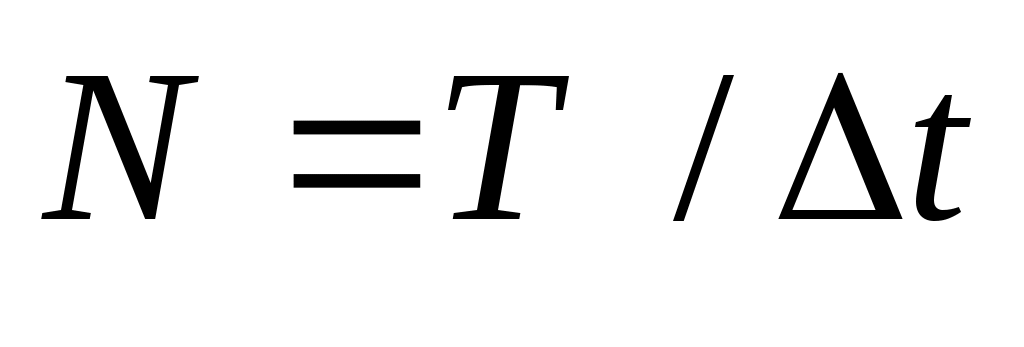 — число отсчетов на интервале длительности сигнала Т. — число отсчетов на интервале длительности сигнала Т.
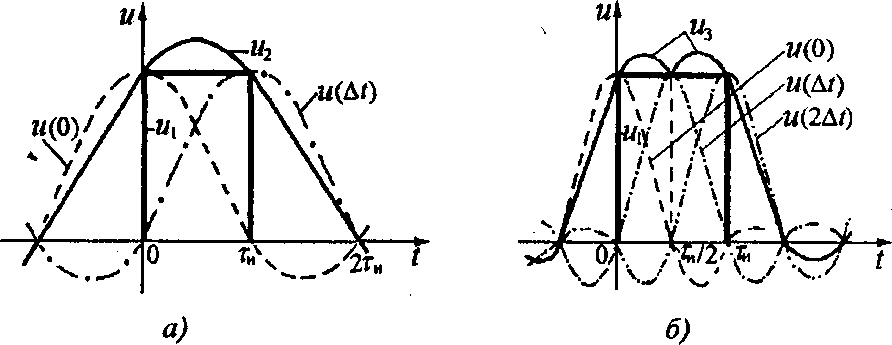
Рис.. Представление прямоугольного импульса отсчетами:
а—двумя; б—тремя.
Пример. Представить аналитически рядом Котельникова прямоугольный импульс напряжения с единичной амплитудой и длительностью 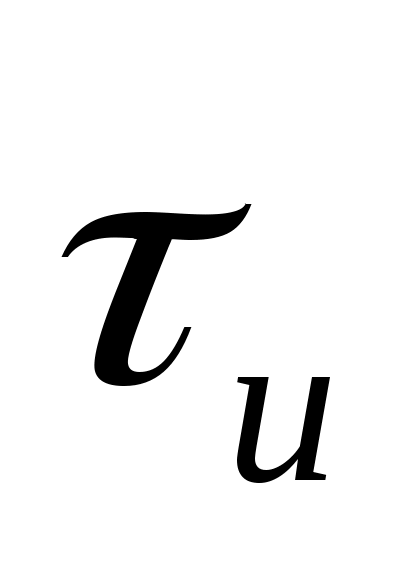 для двух случаев: 1 — спектр аппроксимирующей функции ограничен верхней частотой для двух случаев: 1 — спектр аппроксимирующей функции ограничен верхней частотой 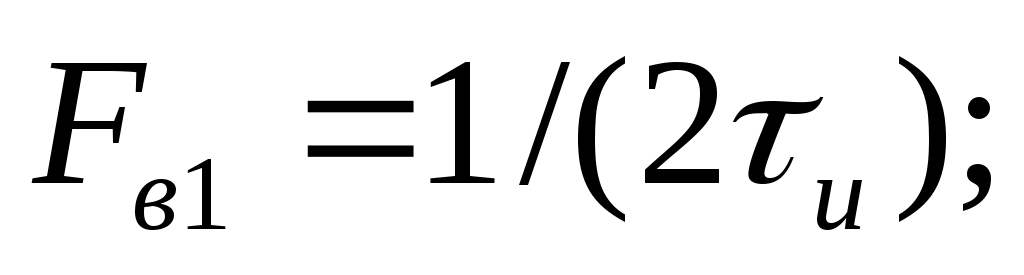 2 — спектр аппроксимирующей функции ограничен верхней частотой 2 — спектр аппроксимирующей функции ограничен верхней частотой 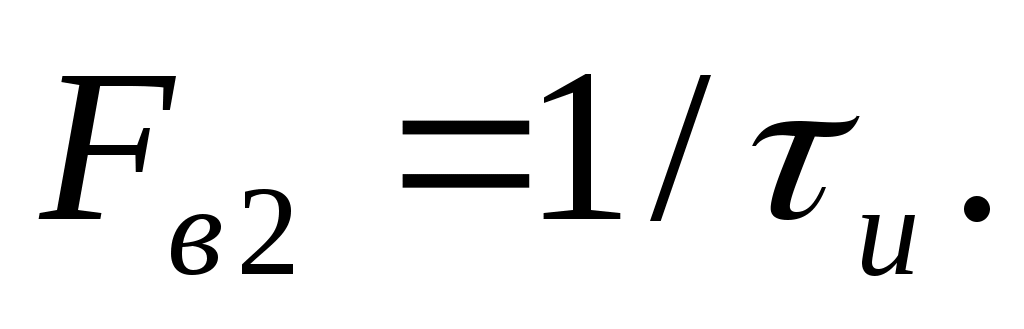
Решение. Для первого из рассматриваемых случаев интервал дискретизации 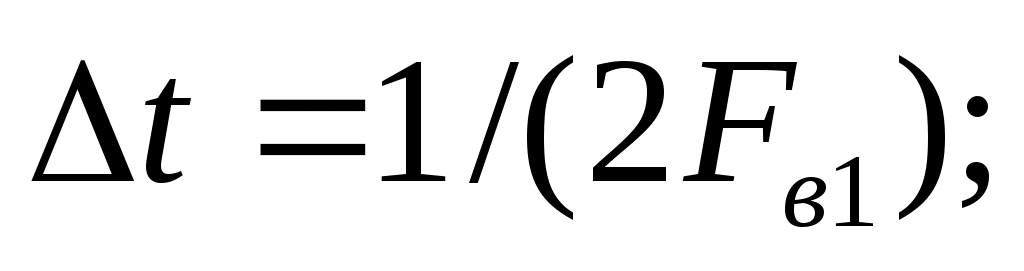 , а значит, импульс будет представлен всего двумя отсчетными значениями — в начале и конце импульса. Подставив в формулу (3.1) требуемые значения амплитуды и длительности импульса, запишем математическую модель аппроксимирующей функции , а значит, импульс будет представлен всего двумя отсчетными значениями — в начале и конце импульса. Подставив в формулу (3.1) требуемые значения амплитуды и длительности импульса, запишем математическую модель аппроксимирующей функции
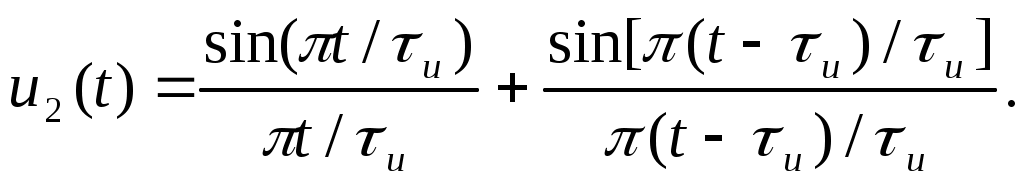
Во втором случае импульс дискретизируется тремя равными отсчетами, производимыми в моменты времени 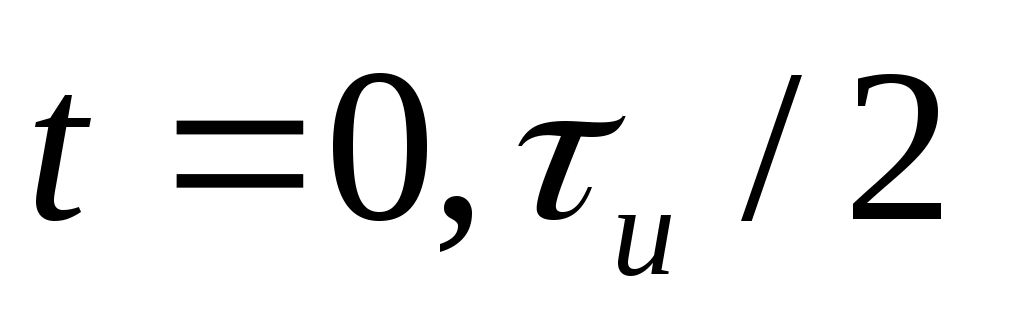 и и 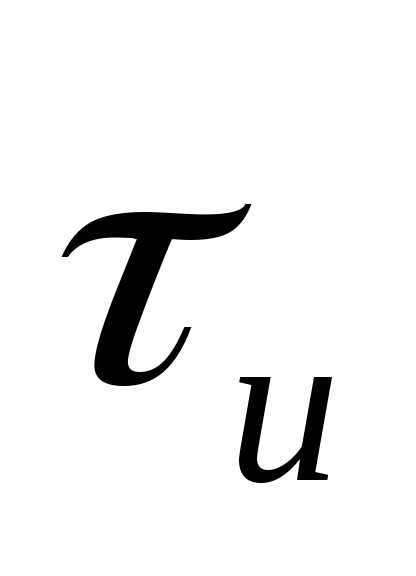 , т.е. в начале, середине и конце импульса. , т.е. в начале, середине и конце импульса.
Тогда
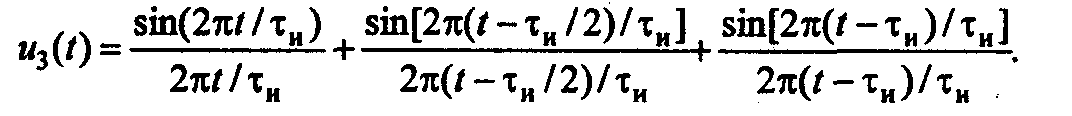
ЭТАПЫ ВЫПОЛНЕНИЯ РАБОТЫ
Для каждого значения  =1с и =1с и  =2с записать значения =2с записать значения 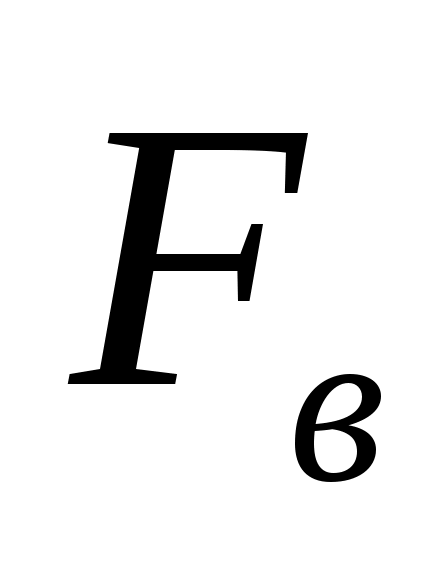
Построить графики базисные функции Котельникова для обоих значений  =1с и =1с и  =2с в одних осях. =2с в одних осях.
Записать аналитические выражения разложения в ряд Котельникова для обоих значений  =1с и =1с и  =2с. =2с.
Построить графики аппроксимаций случайного сигнала рядом Котельникова и сравнить их.
Сделать вывод по результатам работы.
ВАРИАНТЫ
№вар
|
x(t)
|
t,c
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
|
2,2
|
-4,8
|
4,6
|
-1,0
|
1,7
|
0,1
|
1,7
|
2,7
|
-3,3
|
-4,0
|
-0,3
|
|
-3,7
|
-4,1
|
-4,8
|
-1,7
|
1,6
|
-0,3
|
4,9
|
4,8
|
-0,9
|
-2,6
|
3,9
|
|
4,2
|
3,9
|
2,2
|
-2,2
|
-1,0
|
-1,7
|
4,1
|
-1,1
|
-4,0
|
-1,7
|
-1,0
|
|
4,6
|
1,4
|
-3,7
|
-3,1
|
-3,3
|
-4,9
|
-0,4
|
1,1
|
-2,5
|
2,6
|
2,7
|
|
3,2
|
0,2
|
-4,1
|
1,2
|
-0,6
|
-0,3
|
-4,4
|
3,8
|
3,5
|
4,2
|
4,8
|
|
-3,0
|
-3,2
|
1,4
|
3,1
|
-0,3
|
-1,5
|
-0,2
|
3,7
|
4,9
|
3,7
|
-1,7
|
|
3,6
|
2,7
|
2,3
|
-4,6
|
0,0
|
2,8
|
-4,0
|
3,8
|
-0,6
|
2,9
|
1,9
|
|
0,3
|
-0,2
|
2,3
|
-4,0
|
-3,0
|
1,9
|
-1,5
|
-2,7
|
-0,8
|
2,5
|
4,2
|
|
1,3
|
3,4
|
-3,9
|
-3,8
|
3,9
|
-3,5
|
-1,4
|
1,6
|
-4,0
|
1,1
|
1,2
|
|
3,0
|
-2,0
|
2,8
|
4,5
|
2,3
|
0,0
|
3,8
|
-2,6
|
0,5
|
1,0
|
0,1
|
|
-0,4
|
0,2
|
1,5
|
4,5
|
-1,4
|
0,6
|
3,3
|
-0,7
|
1,0
|
2,6
|
0,8
|
|
-0,1
|
-2,7
|
0,8
|
-2,5
|
1,1
|
-4,5
|
3,5
|
0,4
|
-2,8
|
-1,9
|
1,8
|
|
2,5
|
-5,0
|
4,4
|
1,8
|
2,3
|
-1,2
|
-2,3
|
5,0
|
-0,9
|
-1,2
|
0,6
|
|
2,2
|
-1,9
|
3,7
|
-4,7
|
0,2
|
-1,1
|
-1,8
|
0,5
|
3,7
|
-0,2
|
-4,0
|
|
4,9
|
3,4
|
4,2
|
1,4
|
0,2
|
-1,0
|
0,1
|
2,5
|
-2,5
|
2,1
|
-4,4
|
|
0,7
|
-4,6
|
-3,1
|
3,3
|
-0,3
|
-0,6
|
2,6
|
-1,5
|
-2,5
|
-2,9
|
2,9
|
|
1,2
|
-1,2
|
2,9
|
2,6
|
3,3
|
0,2
|
3,3
|
2,8
|
-2,8
|
1,8
|
1,0
|
|
-3,4
|
3,9
|
0,3
|
4,9
|
3,4
|
0,3
|
1,5
|
1,5
|
2,3
|
2,0
|
-4,7
|
|
-0,4
|
4,5
|
-1,4
|
-0,9
|
-0,9
|
-3,3
|
-1,3
|
-2,3
|
2,6
|
4,7
|
1,1
|
|
4,0
|
-2,5
|
-0,5
|
-4,2
|
-2,2
|
-2,1
|
2,6
|
-2,0
|
-0,7
|
-2,2
|
2,3
|
|
4,4
|
4,0
|
0,7
|
1,8
|
1,8
|
-4,0
|
-2,3
|
-1,1
|
-3,8
|
-3,3
|
-3,5
|
|
2,7
|
3,3
|
1,6
|
1,4
|
-3,1
|
0,2
|
-1,7
|
2,8
|
0,6
|
-2,2
|
3,3
|
|
3,0
|
-2,8
|
1,5
|
-3,0
|
3,0
|
3,3
|
-4,0
|
-2,7
|
2,3
|
-4,1
|
-3,7
|
|
-1,3
|
4,3
|
-4,4
|
-1,7
|
3,7
|
-1,9
|
-1,2
|
-1,4
|
0,3
|
3,1
|
-3,6
|
|
1,0
|
-0,7
|
3,0
|
2,2
|
-2,1
|
4,9
|
4,3
|
4,4
|
3,7
|
4,2
|
-0,1
|
|
-2,7
|
1,1
|
-2,5
|
-2,5
|
1,8
|
-3,9
|
-0,9
|
3,1
|
-0,9
|
-3,8
|
-3,0
|
|
3,0
|
-3,7
|
-2,7
|
-3,0
|
4,7
|
4,9
|
-4,5
|
-4,0
|
1,4
|
-4,4
|
2,5
|
|
-1,7
|
4,9
|
4,5
|
4,1
|
0,5
|
0,1
|
3,0
|
-1,1
|
2,2
|
-3,1
|
1,8
|
|
3,7
|
4,2
|
-4,0
|
4,2
|
-3,5
|
-0,9
|
0,1
|
4,2
|
-1,5
|
2,3
|
2,4
|
|
-3,7
|
-3,7
|
-3,4
|
-3,6
|
-1,2
|
2,4
|
-3,6
|
1,5
|
0,2
|
0,6
|
3,0
| 31 | 4,1 | 3,8 | 2,2 | -2,1 | -1,5 | -1,7 | -1 | 0.5 | 1,2 | -4,0 | -1,0 | 32 | -3,2 | 1,4 | 3,1 | -0,3 | -1,3 | -0,2 | 3,7 | 4,9 | 3,7 | 1,3 | -0,7 | 33 | 2,7 | 2,3 | -4,6 | -2,0 | 0,0 | 2,8 | 4,0 | -0,6 | 2,9 | 1,9 | 0,5 | 34 | 0,3 | -0,2 | 0,0 | 2,3 | -4,0 | -3,0 | 1,9 | -1,5 | -2,7 | -0,8 | 2,5 | 35 | -0,1 | -2,7 | 0,8 | -2,3 | 1,5 | -4,7 | 3,6 | 0,4 | -3,1 | -1,9 | 1,8 | 36 | 2,2 | -1,8 | 3,7 | -4,8 | 0,3 | -1,5 | -1,9 | 0,5 | 3,7 | -0,4 | -4,0 | 37 | 3,0 | -2,0 | 2,8 | 4,5 | 2,4 | 0,0 | 3,8 | -2,7 | 0,6 | 1,0 | 0,3 | 38 | 2,0 | 1,6 | 1,1 | 0,0 | -0,4 | -1,3 | -3,1 | 0,0 | 1,6 | 1,8 | 3,1 | 39 | 1,5 | -0,7 | -2,1 | -4,1 | 1,6 | 3,1 | 0,4 | 0,0 | -3,1 | -1,7 | 0,7 | 40 | 1,3 | 3,4 | 3,9 | -3,8 | 3,9 | -3,5 | -1,4 | 1,6 | -4,0 | 1,1 | 1,2 | |
 Скачать 155.5 Kb.
Скачать 155.5 Kb.