Финансовые задачи. ФИНАНСОВЫЕ ЗАДАЧИ. 2. Кредиты 1 Погашение кредита равными долями
 Скачать 1.35 Mb.
|
2. Кредиты2.1 Погашение кредита равными долямиЗадача 1 31 декабря 2017 года Сергей взял в банке 2648000 рублей в кредит под 10% годовых. Схема выплат кредита следующая — 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 10%), затем Сергей переводит в банк x рублей. Какой должна быть сумма x, чтобы Сергей выплатил долг тремя равными платежами (то есть за три года)? Решение 1 января 2018 года Сергей будет должен банку не только 2648000 руб., но и 10% от этой суммы, т.е. 2648000 + 0,1*2648000 = 1,1*2648000 руб. Затем Сергей выплачивает х руб. и остается должен (1,1*2648000 – х) руб. 1 января 2019 года Сергей будет должен банку оставшуюся сумму плюс проценты на нее, то есть (1,1*2648000 – х) + 0,1*(1,1*2648000 – х) = 1,1*(1,1*2648000 – х). Затем выплачивается снова сумма в х руб., и остаток долга будет составлять (1,1*(1,1*2648000 – х) – х) руб. Наконец, 1 января 2020 года банк еще раз начисляет проценты на остаток долга, в результате чего Сергей должен (1,1*(1,1*2648000–х)–х)+0,1*(1,1*(1,1*2648000–х)–х)=1,1*(1,1*(1,1*2648000 – х)-х) руб. В течение года Сергей в последний раз выплачивает х руб., после чего кредит считается погашенным (то есть остаток долга равен 0). Приведенные рассуждения удобно представить в виде таблицы ДОЛГ-ВЫПЛАТА-ОСТАТОК
 В приведенной таблице ОСТАТОК = ДОЛГ - ВЫПЛАТА. Из данных правого столбца составим уравнение: 1,1*(1,1*(1,1*2648000 –х) – х) – х = 01,1* (1,1*1,1*2648000 – 1,1х – х) – х = 0 1,1*1,1*1,1*2648000 – 1,21х – 1,1х – х = 0 1,331*2648000 = 3,31х Х=1064800 Ответ: 1064800 руб. Задача 2 В сентябре Федор взял кредит в 1,5 млн. руб. По условиям договора: - каждый январь долг возрастает на 10% по сравнению с концом предыдущего года; - с февраля по август каждого года Федор выплачивает часть долга. На какое минимальное количество лет может взять кредит Федор, чтобы не выплачивать более 450 тыс. руб. в год? Решение В явном виде нам не указано, что гасить кредит нужно равными долями, однако, это тот же тип задачи. Во-первых, логично, что чем больше мы выплачиваем, тем быстрее погасим кредит, а, во-вторых, у нас есть верхнее ограничение по сумме выплат – 450 тыс. руб. Значит, будем выплачивать по максимуму в 0,45 млн., чтобы расплатиться как можно быстрее. Составим таблицу, как в предыдущей задаче (для удобства все суммы будем считать в млн. руб.):
После n лет Федор расплатится по кредиту, то есть его остаток долга будет равен 0 (при решении может получиться и отрицательное число, это означает, что в последний год Федору необязательно выплачивать 450 тыс. руб., а достаточно меньшей суммы). Из данных правого столбца для n-го года составим уравнение: 1,1n*1,5 – 0,45*1,1n-1 - 0,45*1,12 – 0,45*1,1 – 0,45 = 0 1,1n*1,5 – 0,45*(1+1,1+1,12+….+1,1n-1)=0 В 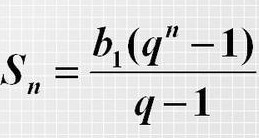 ыражение в скобках – это сумма n членов геометрической прогрессии с первым членом b1=1 и последним членом bn=b1*qn-1. Применяя формулу для вычисления суммы n членов геометрической прогрессии, получим:1,1n*1,5 – 0,45*(1,1n-1)/(1,1-1)=0 1,1n*1,5 – 4,5*1,1n +4,5=0 1,1n = 1,5 4 Значит, Федор погасит кредит за 5 лет. Ответ: 5.  Несмотря на явную простоту такого подхода, имеется «подводный камень»: не всегда учащимся удается доказать свое умение строить математическую модель, есть риск, что при проверке задание могут не зачесть или зачесть не полностью. Поэтому обязательно опишите, откуда взялось число 1,1 и почему мы продолжаем вычисления до появления отрицательного числа.  Иногда подобные задачи можно решить, не выводя формулу для n лет. Достаточно последовательно посчитать остаток долга в цифрах – после 1 года, 2 года и т.д. Как только остаток долга станет 0 или отрицательным, значит, искомый год найден.В нашей задачe получим: после 1 года: 1,1*1,5 – 0,45 = 1,2 после 2 года 1,1*1,2 – 0,45 = 0,87 после 3 года 1,1*0,87 – 0,45 = 0,507 после 4 года 1,1*0,507 – 0,45= 0,1077 после 5 года 1,1*0,1077 – 0,45 = -0,33153 Получив отрицательное число, делаем вывод, что на 5 году кредит будет полностью выплачен. Ознакомьтесь с оформлением подобной задачи в разделе 5. Задачи для самостоятельной работы
|