Финансовые задачи. ФИНАНСОВЫЕ ЗАДАЧИ. 2. Кредиты 1 Погашение кредита равными долями
 Скачать 1.35 Mb.
|
2.2 Равномерное уменьшение долга по сравнению с предыдущим периодомДля данного типа задач существует характерная особенность – при заполнении таблицы мы отталкиваемся от графы «Остаток долга». Поскольку остатки долга за каждый период отличаются друг от друга на равную величину, чтобы найти эту величину достаточно поделить сумму долга на количество таких периодов. Например, если сумма кредита составляет 10 млн руб., а количество лет равно 4, то остатки будут отличаться на 10млн/4 = 2,5 млн. руб., а графа «Остаток долга примет» вид:
 Замечу, что при неизвестной сумме кредита и неизвестном количестве периодов графу «Остаток» можно заполнить последовательностью чисел: S*(n-1)/n, S*(n-2)/n,…..,S*2/n, S/n, 0. Задача 1 В январе планируется взять кредит на 5 месяцев. Условия по договору следующие: - 1-го числа каждого месяца долг возрастает на 15% по сравнению с концом предыдущего месяца; - со 2–го по 14-е число нужно выплатить часть долга; - 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца. Сколько процентов от суммы кредита составит общая сумма выплат за весь срок? Решение Пусть S – сумма кредита. Тогда остатки долга будут отличаться на S/5 руб. Заполним таблицу (сначала графу «Остаток», затем графу «Долг» и только потом «Выплату» как их разность):
Общая сумма выплат (суммируем выплаты 1-5 месяцев): 1,15*S - 4S/5 + 1,15*4S/5 - 3S/5 + 1,15*3S/5 - 2S/5 + 1,15*2S/5 - S/5 + 1,15*S/5 = 1,15*S(1+4/5+3/5+2/5+1/5) – S/5*(4+3+2+1) = 3,45S – 2S = 1,45S. Это означает, что сумма выплат составляет 145% от суммы кредита. Ответ: 145 Задача 2 Взят кредит на 18 месяцев. Условия его возврата таковы: - 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца; - со 2–го по 14-е число нужно выплатить часть долга; - 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца. Какую сумму планируется взять в кредит, если известно, что за первые 9 месяцев нужно выплатить 2048 тыс. руб.? Решение Пусть S – сумма кредита. Тогда остатки долга будут отличаться на S/18 руб. Заполним таблицу на первые 9 месяцев:
В общем виде, для каждого месяца ДОЛГ = 1,02*S*(19-n)/18, ОСТАТОК = (18-n)*S/18, а ВЫПЛАТА = 1,02*S*(19-n)/18 - (18-n)*S/18, где n – номер месяца. Просуммируем выплаты за 9 месяцев и приравняем к данной в условии величине: (1,02*S - 17S/18) + (1,02*17S/18 - 16S/18) + (1,02*16S/18 - 15S/18) +…+ (1,02*11S/18 - 10S/18) + (1,02*10S/18 - 9S/18) = 2048 Сгруппируем отдельно подчеркнутые и неподчеркнутые слагаемые: (1,02*18S/18 + 1,02*17S/18 + 1,02*16S/18 +… + 1,02*11S/18 + 1,02*10S/18) – (17S/18 + 16S/18 + 15S/18 + … +10S/18 + 9S/18) = 2048 1,02*S/18*(18 +17 + … + 10) – S/18*(17 + 16 + … + 9)=1024 Первая скобка – сумма первых 9 членов арифметической прогрессии при a1=10, a9=18. Вторая скобка – тоже сумма первых 9 членов арифметической прогрессии при a1=9, a9=17. П 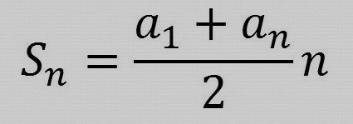 рименяя формулу для суммы n членов арифметической прогрессии, получим:(1,02*S*14*9 – S*13*9)/18 = 2048 S=3200 (тыс. руб.) В ответе, если условие задачи не требует иного, значения лучше указывать в единицах СИ. Ответ: 3 200 000 руб. Задача 3 В июле планируется взять кредит в банке на сумму 7 млн. рублей на некоторый срок (целое число лет). Условия его возврата таковы: 1) каждый январь долг возрастает на 20% по сравнению с концом предыдущего года; 2) с февраля по июнь каждого года необходимо выплатить часть долга; 3) в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года. На сколько лет планируется взять кредит, если известно, что общая сумма выплат после его полного погашения составит 17,5 млн. рублей? Решение Эту задачу можно решить, как ранее, с помощью таблицы ДОЛГ-ВЫПЛАТА-ОСТАТОК, но есть и альтернативный вариант. По моему мнению, он проще для тех, кто хорошо понимает арифметические прогрессии. Обозначим сумму кредита за а0 (это наши 7 млн. руб.) и а1, а2… аn – остатки после 1-го, 2-го, …n-го года. Выплаты же обозначим через х1, х2, … xn. Тогда: а1 = 1,2* а0 - х1 а2 = 1,2* а1 – х2 а3 = 1,2* а2 – х3 … an = 1,2* аn-1 – хn Просуммируем уравнения в системе: а1 + …. + an = 1,2*а0 + 1,2*(а1 +… + аn-1) – (х1 +…+ хn) Сумма х1 +…+ хn = 17,5 по условию задачи, an = 0, так как это - остаток долга в последний год. Числа а1, а2… аn – члены арифметической прогрессии (по условию разность между соседними остатками одинакова). В левой части уравнения получим Sn= (а1+ an)*n/2 В правой части в скобку (а1 +… + аn-1) добавим an. От этого ничего не изменится, так an = 0, но скобка превратится в Sn. Sn = 1,2*7 + 1,2* Sn – 17,5 Sn = 45,5 Значит, 45,5 = (а1+ an)*n/2 => а1=91/n an = 0 = а0 + n*d => d=-7/n С другой стороны, а1 = a0 + d = 7 + d = 7 + (-7/n) Следовательно, справедливо равенство: 91/n = 7 - 7/n n=14 (лет) Ответ: 14 Задачи для самостоятельной работы:
|