БДД. Над ИВК лр 8 (4). Лабораторная работа 8 Логические методы распознавания. Метод сокращённого базиса Цель работы

• Название: Лабораторная работа 8 Логические методы распознавания. Метод сокращённого базиса Цель работы
• Дата: 04.12.2020
• Размер: 50.38 Kb.
• Имя файла: Над ИВК лр 8 (4).docx
• Тип: Лабораторная работа; #156971
• страница: 3 из 6

Аргументы идут в порядке следования, в первой строке имеются перестановки чисел 0 и 1, во второй — перестановки пар чисел, в третьей — четвёрок чисел. Число одинаковых цифр в перестановке равно 2' *, где / — номер строки. Каждую строку базиса можно рассматривать как двоичное число, которое называется изо­бражающим числом аргумента и обозначается знаком #. Каждый столбец базиса также представляет собой двоичное число, равное номеру столбца (от 0 до 7).

Изображающее число переменной Л в базисе (А, В, С):

• 
  А =01010101
  

Для изображающих чисел справедливы операции «И», «ИЛИ» и «НЕ», совер­шаемые поразрядно. Например,

• 
  А л#Я=(01010101)л(00110011) = 00010001;
  
• 
  А v#B = (01010101) v (00110011) = 01110111.
  

Изображающее число булевской функции образуется с помощью соответствую­щих операций над изображающими числами аргументов. Например, если

Е = АуВлС = А + ВС, (17)

то, учитывая (табл. 4), найдём

• 
  £ = 01010101 v(00110011) (00001 111) = 01010101 + 00000011 = 010101 И
  

Операция отрицания («НЕ») для изображающего числа означает замену 0 на 1 и наоборот. Например, если = 01010101, то #А = 10101010.

Использование булевских функций для задач распознавания

Метод сокращённого базиса. Задача распознавания при использовании булевских функций формулируется следующим образом: известны логические связи при­знаков и состояний в виде булевской диагностической функции F(k_t,k₂,...,k_m,D_vD₂,...,D„) = \

Иными словами, по функции признаков следует определить функцию состояний при условии истинности диагностической функции. Ниже приводится пример решения подобной задачи.

Пример 2

Пусть в случае двух признаков и двух состояний логические связи таковы:

1. 
   При состоянии Di появляется признак k_t.
   
2. 
   Обнаружение признака к₂ свидетельствует об отсутствии состояния D_t.
   
3. 
   При состоянии D₂ появляются оба признака.
   

На основании этих сведений булевская диагностическая функция запишется так:

F(A₁,A₂,D₁,D₂) = (D₁ -+A,)a(A₂ ->Ц)л(О₂ лА₂) (18)

Пусть при обследовании обнаружено наличие признака k_t и отсутствие признака к₂. Тогда булевская функция признаков:

G = к_{ лк₂ (19)

Воспользуемся общим методом отыскания булевской функции состояния — ме­тодом сокращенного базиса. Для этого сначала выписываем полный базис:

Таблица 5.

Полный базис булевской диагностической функции четырёх аргументов

Номер столб­ца	0	1	2	э	4	5	6	7	8	9	10	11	12	13	14	15
А/	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1
к2	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1
D,	0	0	0	0	1	1	1	1	0	0	0	0	1	1	1	1
d2	0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1

Далее находим изображающее число для булевской диагностической функции: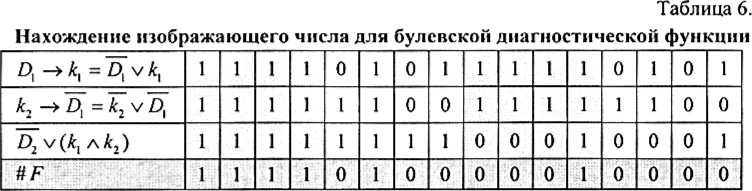


В изображающем числе для функции F, полученном в соответствии с формулой (18), единицы стоят в столбцах, отражающих возможные (не противоречащие F) сочетания признаков и диагнозов. По булевской функции признаков G (19) А, = 1, к₂ = 0. Такое сочетание признаков при F = 1 имеется только в столбцах 1 и 5 (для столбцов 9 и 13 с таким же сочетанием значений А/ и к₂ значение F = 0 , следовательно, эти столбцы противоречат диагностической функции и исключа­ются из рассмотрения). Для столбца 1 D, = 0 и О₂ = 0, а для столбца 5 Z), = 1 и D₂ =0.

Таким образом, булевская функция диагнозов:

/ = (d'₁a'D₂)s_/(D₁a'D₂) = d'₂ (20)

Преобразование равенства (20) можно получить из формул поглощения (16), но его легко найти с помощью изображающих чисел. Так как рассмотрение относит­ся к двум булевским величинам, то базис £>,0101 £>₂001 1

Далее находим:

а£^1000

aD^OIOO

#(£\ a^)v(£), a£Q1100 = #^

В общем случае функциям G и F не противоречат несколько возможных состоя­ний, поэтому имеющихся сведений недостаточно для однозначного решения. В подобной ситуации для выбора решения используются другие методы распозна­вания, например, метод Байеса.

Порядок выполнения работы:

1. 
   Записать булевскую диагностическую функцию