Лабораторная работа 8 Проверка статистической гипотезы о виде распределения. Критерий согласия Пирсона Вариант 7 Задание
 Скачать 148.18 Kb. Скачать 148.18 Kb.
|
|
Лабораторная работа №8 «Проверка статистической гипотезы о виде распределения. Критерий согласия Пирсона» Вариант 7 Задание В следующей выборке представлены данные по цене (X) некоторого товара и количеству (Y) данного товара, приобретаемому домохозяйством ежемесячно в течение года.
1. Построить корреляционное поле (Диаграмма – Точечная). 2. Оценить тесноту связи между переменными с помощью коэффициента корреляции; 3. Найти уравнение регрессии Y по X. 4. Построить линию регрессии на корреляционном поле. 5. Оценить статистическую значимость полученного уравнения регрессии. Решение: Построим корреляционное поле, для этого отметим в системе координат 12 точек, соответствующих данным парам значений этих признаков. 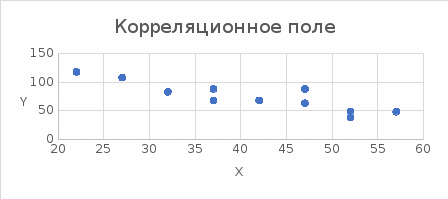 Рис. 1 – Корреляционное поле По расположению точек на корреляционном поле естественно предположить, что зависимость между X и Y близка к линейной. Для построения диаграммы рассеяния в Excel можно воспользоваться командой меню Вставка Точечная диаграмма. На основе анализа поля корреляции видно, что между ценой товара и приобретаемым количеством существует обратная связь, то есть с увеличением цены количество приобретаемых товаров уменьшается. 2. Определим линейный коэффициент корреляции и проверим его на значимость. Составим вспомогательную таблицу:
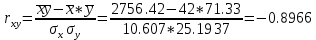 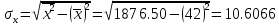 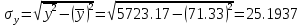 Рассчитаем коэффициент детерминации: 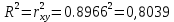 Коэффициент корреляции |r|=0.8966 находится в интервале 0,75-0,95, это указывает на сильную, тесную линейную связь между признаками. Так как r<0, это означает, что связь между ценой и количество приобретаемого обратная, то есть с увеличением цены количество приобретаемых товаров уменьшается. Коэффициент детерминации R2=0,8039 показывает, что 80,39% вариации количества приобретаемого товара (Y) объясняется вариацией фактора X– ценой товара, а на долю прочих факторов приходится лишь 19,61%. Проверим значимость коэффициента парной корреляции rxy при уровне значимости α=0,05. 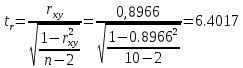 Для определения tкрит может использоваться статистическая функция СТЬЮДРАСПОБР() из MS Excel. При α = 0,05 и степени свободы k = n–2 = 12–2 = 10 tкрит = t1α,n-2 = СТЬЮДРАСПОБР(0,05;10) =2,2281. 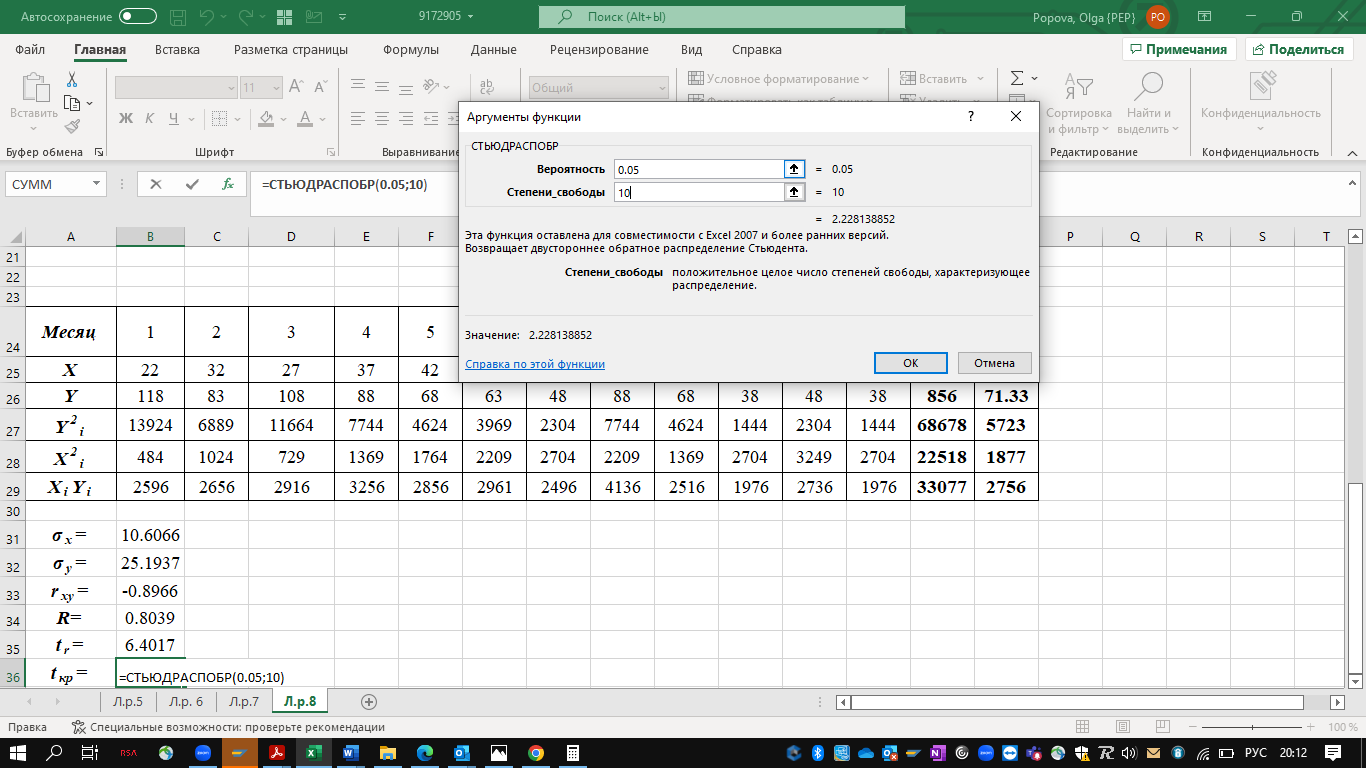 Рисунок 2 - Окно ввода параметров функции СТЬЮДРАСПОБР() MS Excel Так как tr=6,4017>t1α,n-2 =2,2281, то делаем вывод о статистической значимости линейного коэффициента парной корреляции rxy. 3. Определим параметры a и b линейной модели регрессии y=ax+bи наложим ее график на корреляционное поле. Рассчитаем коэффициенты регрессии: 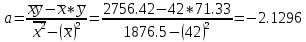 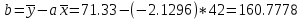 Регрессионное уравнение имеет следующий вид: 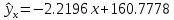 Значение коэффициентов в уравнении регрессии 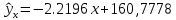 означает, что увеличение цены продукции на 1 усл. ед. приводит в среднем к уменьшению количество приобретаемого товара на 2,2196 ед. означает, что увеличение цены продукции на 1 усл. ед. приводит в среднем к уменьшению количество приобретаемого товара на 2,2196 ед. 4. Изобразим на корреляционном поле график функции 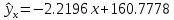 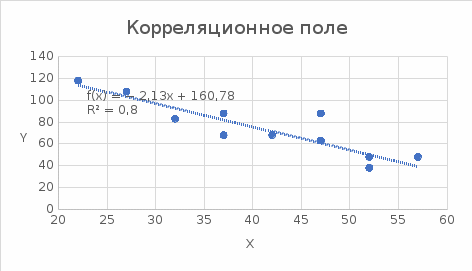 Рис. 3 – График функции 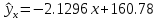 5. Проверяем адекватность полученного уравнения регрессии по критерию Фишера — Снедекора. Находим статистику: 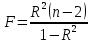 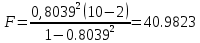 При уровне значимости α=0,05 и числах степеней свободы k1=1, k2=n-2=10-2=10 по таблице критических значений точек распределения Фишера – Снедекора находим: 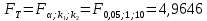 Так как 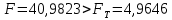 , то модель адекватна. Следовательно, зависимость между ценой X и количеством приобретаемых товаров Y описывается уравнением , то модель адекватна. Следовательно, зависимость между ценой X и количеством приобретаемых товаров Y описывается уравнением 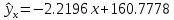 . . |
