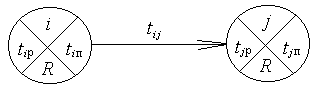|
|
Лабораторная работа 8 задача сетевого планирования
Лабораторная работа № 8
Цель работы: построение и расчет сетевой модели выполнения комплекса работ, определение продолжительности критического пути.
1. Общие сведения
Актуальной задачей производства является определение продолжительности выполнения комплекса операций (работ), которые входят в тот или иной технологический процесс. При этом в качестве известных величин выступают продолжительность каждой операции, а также данные о том, какие работы должны быть в обязательном порядке закончены до начала выполнения операций. Решить данную задачу позволяет построение так называемой сетевой модели – графического изображения последовательности выполнения операций во времени. Сетевая модель также позволяет выявить работы, несвоевременное выполнение которых приводит к срыву графика выполнения комплекса операций в целом, и, напротив, работы, которые могут быть отложены на какое-то время. Таким образом обеспечивается рациональное планирование работы предприятия и его подразделений.
2.1. Постановка задачи
Бригада рабочих выполняет комплекс из m работ, для каждой из работ известна продолжительность, а также то, какие работы должны быть в обязательном порядке выполнены перед началом данной работы. Требуется построить и рассчитать сетевую модель, определить минимальную продолжительность выполнения всего комплекса работ.
2.2. Основные понятия, условные обозначения, правила
построения и расчета сетевой модели
Основными элементами сетевой модели являются события и работы. Различают работы действительные и фиктивные. Под действительными работами понимаются любые действия, реализация которых требует затрат труда, времени и ресурсов других видов. Фиктивныеработы отражают существование зависимостей между работами, не связанными между собой непосредственно. Продолжительность фиктивной работы равна нулю. Событием называют факт завершения или начала работы или нескольких работ.
При построении сетевой модели приняты следующие обозначения:
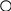 – событие; – событие;
– фиктивная работа;
––––– – действительная работа.
Путь – любая непрерывная последовательность между двумя событиями. Полный путь – путь от исходного до завершающего события. Критический путь – полный путь, который имеет наибольшую продолжительность по времени. Критический путь определяет полную продолжительность выполнения всего комплекса работ.
Говорят, что работа А «опирается» на работу Б, если А не может быть выполнена раньше, чем закончится Б. Например, если работа А – это прессование ДСтП, работа Б – формирование стружечного ковра.
Работами первого ранга называют такие, которые не опирающиеся ни на какие другие работы. Работы второго ранга – это работы, опирающиеся хотя бы на одну из работ первого ранга. Работы третьего ранга – это работы, опирающиеся хотя бы на одну из работ второго ранга. И так далее.
Правила построения сетевой модели:
все стрелки, изображающие работы, ориентируются слева направо;
индекс события соответствует индексу работы, завершением которой является данное событие;
построение модели начинают с построения нулевого события, соответствующего началу выполнения комплекса работ;
на нулевое событие опираются работы первого ранга. Построение работ и событий их завершения проводят в порядке возрастания ранга работ;
работа не может быть построена раньше, чем все работы, на которые она опирается;
если две работы начинаются от одного события, а третья может начаться только по завершении обеих (т. е. по условию опирается на них), то на модели должна быть введена фиктивная работа и еще одно событие, которым завершается одна из двух первых работ.
Например, пусть работа В опирается на работы А и Б. Из работ А и Б следует выбрать ту, которая заканчивается позднее. Это работа Б. Тогда стрелка работы В на сетевой модели будет исходить из события, завершающего работу Б, а события, завершающие работы А и Б, будут соединены фиктивной работой. Стрелка фиктивной работы, как и все стрелки на сетевой модели, направлена в соответствии с направлением оси времени, т. е. от события А к событию Б (рис. 8.1);
 Рис. 8.1. Построение фиктивной работы
на сетевой модели не может быть циклов;
стрелки на сетевой модели по возможности не должны пересекаться.
Для расчета сетевой модели вводятся следующие обозначения (рис. 8.2):
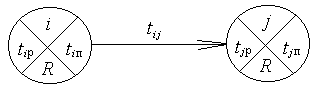 Рис. 8.2. Обозначения, используемые при расчете сетевой модели:
i – индекс события, с которого начинается работа; j – индекс события,
которым заканчивается работа; tij – продолжительность работы; tiр – ранний
срок наступления события; tiп – поздний срок наступления события; R – резерв
Ранний срок наступления события равен наибольшей суммарной продолжительности работ, ведущих к данному событию. Ранний срок наступления исходного (нулевого) события равен нулю. Ранний срок наступления событий первого ранга равен продолжительности соответствующей работы первого ранга. При построении сетевой модели с использованием оси времени ранний срок наступления события равен координате события на временной оси.
Поздний срок наступления завершающего события равен раннему. Для остальных событий поздний срок определяется вычитанием из продолжительности критического пути наибольшего по продолжительности пути, следующего за событием. Другими словами, из возможных поздних сроков наступления события всегда выбирается наименьший.
Резерв события равен разности между поздним и ранним сроком наступления данного события
Критический путь сетевой модели проходит через события, имеющие нулевой резерв.
Подкритическими называют полные пути, длина которых отличается от критических не более чем на 10%.
Для расчета сетевой модели необходимо выполнить следующую последовательность действий:
вычертить сетевую модель комплекса работ;
рассчитать (или записать, если построение сетевой модели осуществлялось с использованием временной оси) ранние сроки наступления событий. При этом нужно продвигаться от исходного к завершающему событию;
проставить поздний срок наступления завершающего события, равный раннему;
рассчитать поздние сроки наступления событий, продвигаясь в обратном порядке – от завершающего события к исходному;
рассчитать резервы событий;
провести критический путь через события с нулевыми
резервами;
принять минимальную продолжительность выполнения всего комплекса работ равной длине критического пути.
|
|
|
 Скачать 229 Kb.
Скачать 229 Kb.
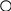 – событие;
– событие;