Лаба 9. Лабораторная работа № 9. Лабораторная работа 9 Оптимизация расчета аналоговых фнч с использованием функции цели и встроенных функций пакета программы Mathcad
 Скачать 89.21 Kb. Скачать 89.21 Kb.
|
|
Лабораторная работа № 9 Оптимизация расчета аналоговых ФНЧ с использованием функции цели и встроенных функций пакета программы «Mathcad». 1. Цель работы Изучить способы оптимизации аналоговых ФНЧ с применением средств программной среды «Mathcad». 2. Подготовка к работе Изучить по литературе [1] содержание страниц 219-238, 397, 398 и материал лекции по данной теме. 3. Литература [1] – В.И.Качанов. Радиотехника плюс компьютер плюс Mathcad. М. 2001. – Конспект лекций по дисциплине ОКП и МРЭС. 4. Пояснения к работе Оптимизация относится к классу задач нелинейного программирования. Сущность процесса оптимизации сводится к поиску наилучшего решения определенной задачи – характеристик устройств или процесса – согласно выбранному критерию Несмотря на все разнообразия критериев их можно свести к единой математической записи – функции цели, которая в концентрированной форме отражает смысл решенной задачи по оптимизации устройства. В качестве функции цели при проектировании ФНЧ можно было бы принять получение минимального значения порядка фильтра при условии, что он удовлетворяет всем остальным требованиям. Поэтому в качестве функции цели примем минимум отклонения группового времени запаздывания от допустимого на двух частотах (0,64 – нормированная частота, на которой допустимая задержка минимальна – 5мс и 1 – нормированная частота среза, где обычно наблюдается увеличение групповой задержки). Принимая: Nb – порядок фильтра Баттерворта; τb(0,64,Nb) – групповое время запаздывания на w= 0,64; τb(1,Nb) – групповое время запаздывания на w=1, записываем функцию цели в виде Y(Nb):=| τb(0,64,Nb) – 5 |+| τb(1,Nb) – 8| Поиск минимума этой функции позволяет определить требуемый порядок Nb для обеспечения допустимого группового запаздывания. Однако, полученное значение Nb может оказаться недостаточным для обеспечения требований по Amin и Amax. В этом случае производится аналогичная процедура для фильтра Чебышева. Допустимые нормы на групповое время запаздывания приведены в таблице1. Таблица1
5. Порядок выполнения работы В данном пункте необходимо для своего варианта значениям Amin, Amax, ώn для ФНЧ определить оптимальное значение порядка аналогового ФНЧ Братерворта (из условий допустимой групповой задержки (таблица 1) и реализуемости на непрезиционных элементах (N< 6-8) Решение задачи провести для данных значений параметров из таблицы 2 и с использованием для оптимизации встроенных функций «f(x)» программной среды Mathcad. В качестве критерия оптимизации следует выбрать минимум отклонения получаемого группового времени запаздывания сигнала на входе фильтра на частотах 6400 Гц (минимальное допустимое время задержки по стандарту на этой частоте) и fpn (частота среза), где фильтр дает наибольшее время запаздывания. Сначала определяется требуемый порядок ФНЧ Баттерворта и производится проверка соответствия получаемого времени запаздывания нормой, а затем определяется порядок фильтра Чебышева и проводится соответствующая проверка для него. По результатам проверки выбирается фильтр, имеющий наименьший порядок и удовлетворяющий требованиям по задержке. Возможны варианты значений параметров, для которых оба исследуемых фильтра не будут удовлетворять требованиям по допустимой групповой задержке сигнала. В таблице 2 даны варианты значений, где Amin- - затухание на граничной частоте полосы непропускания fpn; Amax - неравномерность в полосе пропускания от 0 до fpp; ώn – fpn/fpp. Таблица 2
Продолжение таблицы 2
5.1. Введем обозначение параметров wzcp – нормированная частота среза (frpпн/fв) Nb – порядок аналогового ФНЧ Баттерворта Nc – порядок цифрового ФНЧ Чебышева w- текущая частота Hb(w) – АХЧ ФНЧ Баттерворта Hc(w) – АХЧ ФНЧ Чебышева b(w) – τ групповое время запаздывания ФНЧ Баттерворта τc(w) – групповое время запаздывания ФНЧ Чебышева Amiv1 – требуемое рабочее ослабление на частоте среза для фильтра Баттерворта Amiv2 – требуемое рабочее ослабление на частоте среза для фильтра Чебышева Amax1 и Amax2 – допустимые неравномерности в полосе пропускания фильтров Баттерворта и Чебышева 5.2 Задание начальных значений параметров  Эти значения выбираются из таблицы 2 по номер бригады. Индекс 2 относится к фильтру Чебышева. 5.3 Допустимые значения ГВЗ ФНЧ для аудиосигналов (из норм для трактов звукового вещания).   Рисунок 1 Рисунок 1 построен путем кусочно-линейной интерполяции. 5.4 Расчет параметра Nb с помощью функции цели Запишем выражения, необходимые для определения τb(w). Сначала определяется минимально необходимый порядок фильтра, удовлетворяющий заданным параметрам. 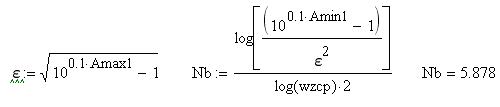 Т.е. требуется ФНЧ Баттерворта 6-го порядка. Далее следует определить наибольший порядок фильтра, удовлетворяющий требованиям по групповой задержке. 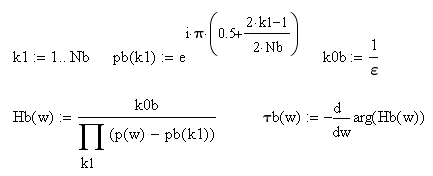  Запишем функцию цели для нахождения максимального порядка ФНЧ, удовлетворяющего требованиям по t. Нормированные частоты выбраны 0.64 (по минимально допустимому значению групповой задержки) и 1 (соответствует Fb). Будем искать минимум функции цели, при котором задержка не превышает допустимые значения. Введем пределы варьируемых параметров с помощью ключевого слова Given. 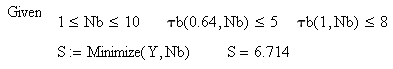 Поскольку N – целое число и N не может быть меньше 6 для удовлетворения требований по затуханию, то принимаем N=7 и производим проверку групповой задержки на требуемых частотах. Таким образом, допустимо использование ФНЧ Баттерворта порядка 7, а требуется Nb=6. Следовательно, для ФНЧ Баттерворта следует принять порядок фильтра равным 6. Определим теперь требуемый порядок ФНЧ Чебышева. 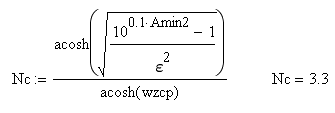 Т.е. требуется ФНЧ Чебышева 4-го порядка. Для него произведем проверку получаемого времени задержки на нормированных частотах 0.64 и 1. Задание начальных параметров    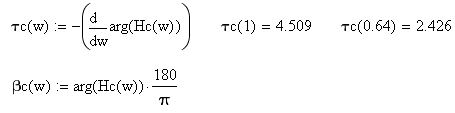 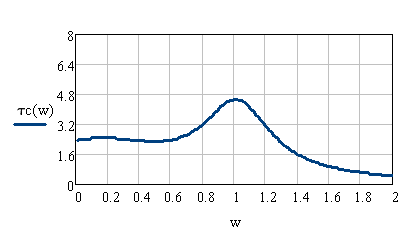 Рисунок 2 Таким образом, ФНЧ Чебышева 4-го порядка удовлетворяет всем предъявленным требованиям. 6. Контрольные вопросы Дать понятие функции цели. Из каких соображений стоится функция цели в данной работе? Сущность процесса оптимизации. Почему нужны нормы на групповое время запаздывания? Почему порядок аналоговых фильтров не должен превышать значения 6-8? Откуда следует, что в рассмотренном примере ФНЧ Чебышева удовлетворяет всем предъявленным требованиям? |
