Лабораторная работа 5. Двумерный массив (2 задания). Лабораторная работа Двумерный массив
 Скачать 42.97 Kb. Скачать 42.97 Kb.
|
|
Лабораторная работа 5. Двумерный массив. Задание 1: Ввести с консоли n-размерность матрицы a [n] [n]. Задать значения элементов матрицы в интервале значений от -n до n с помощью датчика случайных чисел. Баллы (90-100) 1. Упорядочить строки (столбцы) матрицы в порядке возрастания значений элементов k-го столбца (строки). 2. Выполнить циклический сдвиг заданной матрицы на k позиций вправо (влево, вверх, вниз). 3. Найти и вывести наибольшее число возрастающих (убывающих) элементов матрицы, идущих подряд. 4. Найти сумму элементов матрицы, расположенных между первым и вторым положительными элементами каждой строки. 5. Транспонировать квадратную матрицу. 6. Вычислить норму матрицы. 7. Повернуть матрицу на 90 (180, 270) градусов против часовой стрелки. 8. Вычислить определитель матрицы. 9. Построить матрицу, вычитая из элементов каждой строки матрицы ее среднее арифметическое. 10. Найти максимальный элемент (ы) в матрице и удалить из матрицы все строки и столбцы, его содержащие. 11. Уплотнить матрицу, удаляя из нее строки и столбцы, заполненные нулями. 12. В матрице найти минимальный элемент и переместить его на место заданного элемента путем перестановки строк и столбцов. 13. Преобразовать строки матрицы таким образом, чтобы элементы, равные нулю, располагались после всех остальных. 14. Найти количество всех седловых точек матрицы. (Матрица А имеет седловую точку Аi, j, если Аi, j является минимальным элементом в i-й строке и максимальным в j-м столбце). 15. Перестроить матрицу, переставляя в ней строки так, чтобы сумма элементов в строках полученной матрицы возрастала. 16. Найти число локальных минимумов. (Соседями элемента матрицы назовем элементы, имеющие с ним общую сторону или угол. Элемент матрицы называется локальным минимумом, если он строго меньше всех своих соседей.) 17. Найти наименьший среди локальных максимумов. (Элемент матрицы называется локальным минимумом, если он строго меньше всех своих соседей.) 18. Перестроить заданную матрицу, переставляя в ней столбцы так, чтобы значения их характеристик убывали. (Характеристикой столбца прямоугольной матрицы называется сумма модулей его элементов.) 19. Путем перестановки элементов квадратной вещественной матрицы добиться того, чтобы ее максимальный элемент находился в левом верхнем углу, следующий по величине — в позиции (2, 2), следующий по величине — в позиции (3, 3) и т. д., заполнив таким образом всю главную диагональ. Задание 2. Дана матрица  . Найти сумму среднего арифметического каждого столбца. . Найти сумму среднего арифметического каждого столбца.2 Дана матрица  . Найти сумму элементов по каждой строке и произведение элементов главной диагонали. . Найти сумму элементов по каждой строке и произведение элементов главной диагонали.3 Вычислить сумму элементов матрицы  , расположенных над главной диагональю. , расположенных над главной диагональю.4 Определить количество положительных и отрицательных элементов матрицы  . Вывести на печать их индексы. . Вывести на печать их индексы.5 Определить количество положительных элементов каждого столбца матрицы 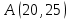 и запомнить их в одномерном массиве и запомнить их в одномерном массиве 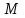 . .6 Найти наибольший элемент матрицы 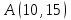 и номер строки и столбца, в которых он находится. Получить вторую матрицу перемножив наибольший элемент на все элементы исходной матрицы. и номер строки и столбца, в которых он находится. Получить вторую матрицу перемножив наибольший элемент на все элементы исходной матрицы.7 Получить векторный столбец 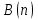 , элементы которого являются наибольшими по модулю элементов строк исходной матрицы , элементы которого являются наибольшими по модулю элементов строк исходной матрицы  . .8 Дана матрица  . Получить векторный столбец, элементы которого являются наименьшими по модулю побочной диагонали исходной матрицы. . Получить векторный столбец, элементы которого являются наименьшими по модулю побочной диагонали исходной матрицы.9 Дана матрица  . Найти сумму элементов, принадлежащих главной диагонали матрицы, разделив ее на максимальный диагональный элемент. . Найти сумму элементов, принадлежащих главной диагонали матрицы, разделив ее на максимальный диагональный элемент.10 Найти максимальный элемент матрицы  среди элементов, находящихся выше главной диагонали. среди элементов, находящихся выше главной диагонали.11 Найти минимальный элемент матрицы  среди элементов, находящихся ниже побочной диагонали. среди элементов, находящихся ниже побочной диагонали.12 Найти разность между максимальным элементом, принадлежащим главной диагонали, и минимальным элементом, принадлежащим вспомогательной диагонали  . .13 Дана матрица  . Найти сумму нечетных элементов матрицы и произведение элементов, находящихся на главной диагонали. . Найти сумму нечетных элементов матрицы и произведение элементов, находящихся на главной диагонали.14 Получить новую матрицу путем деления всех элементов исходной матрицы  на элемент, наименьший по модулю. на элемент, наименьший по модулю.15. Найти среднее арифметическое положительных элементов каждого столбца матрицы  при условии, что в каждом столбце есть хотя бы один положительный элемент. при условии, что в каждом столбце есть хотя бы один положительный элемент.16. Вычислить суммы элементов каждой строки матрицы  , определить наименьшее значение этих сумм и номер соответствующей строки. , определить наименьшее значение этих сумм и номер соответствующей строки.17. Из матрицы  построить матрицу построить матрицу  , поменяв местами строки и столбцы. Вычислить суммы каждой строки новой матрицы. Найти среди сумм наибольшую сумму. , поменяв местами строки и столбцы. Вычислить суммы каждой строки новой матрицы. Найти среди сумм наибольшую сумму. |
