лабораторная математический маятник. Отчет по ЛР№6. Лабораторная работа фпо6 дифракция лазерного света на сетке. Определение параметров сетки. Цель работы изучить явление дифракции на двухмерной решётке (сетке), определить
 Скачать 0.75 Mb.
|
|
ОТЧЕТ ЛАБОРАТОРНАЯ РАБОТА ФПО-6 ДИФРАКЦИЯ ЛАЗЕРНОГО СВЕТА НА СЕТКЕ. ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ СЕТКИ. 1.ЦЕЛЬ РАБОТЫ Изучить явление дифракции на двухмерной решётке (сетке), определить параметры сеток с различными размерами ячеек по дифракционной картине и при прямом измерении. 2. ОПИСАНИЕ УСТАНОВКИ И МЕТОДИКИ ЭКСПЕРИМЕНТА Дифракция света на щели исследуется на экспериментальной установке, схематично изображенной на рис.2.1. 3  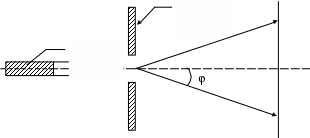 2 1 1 лазер; 2 щель; 3 экран с миллиметровой шкалой Рисунок 2.1 - Принципиальная схема наблюдения дифракции Фраунгофера с использованием в качестве источника света лазера Пучок когерентных параллельных лучей, испускаемых лазером 1, падает на щель 2. Регулируя щель микровинтом, можно ограничить фронт волны и вырезать лишь узкий плоский участок. В этом случае за щелью образуется поле вторичных волн, которые создают дифракционную картину, наблюдаемую на экране 3, отстоящем достаточно далеко от щели. 3. ОСНОВНЫЕ РАСЧЕТНЫЕ ФОРМУЛЫ Если на ширине щели при некотором угле φ уложится четное число зон Френеля, то при наложении все вторичные волны погасят друг друга. В соответствующем направлении, определяемом углом дифракции φ, интенсивность света будет равна нулю. Эти направления определяются соотношением bsin = ±2m /2, (3.1) где m = 1, 2, 3, 4 – порядок минимума. Если на ширине щели при некотором угле уложится нечетное число зон Френеля, то в этом направлении будет наблюдаться максимум света. Условие максимума дается соотношением bsin = ± (2m + 1) /2, (3.2) где m = 1, 2, 3, 4 – порядок максимума. Интенсивность максимумов уменьшается по закону  (3.3)где  Вычисление углов дифракции φm, tg φm = (2xm)/(2l), (3.5) где 2xm – расстояние между центрами темных полосок, l – расстояние от щели до экрана. Поскольку углы дифракции малы, можно считать верным равенство tg φm ≈ sin φm ≈ φm. (3.6) Длина волны λ можно определяется, если использовать метод наименьших квадратов для проведения прямой 1/φ = f(b). В этом случае λ определяется через угловой коэффициент прямой. 4. РЕЗУЛЬТАТЫ РАБОТЫ И ИХ АНАЛИЗ. 4.1 Задание 1 Таблица 4.1 Данные для зависимости угла дифракции от ширины щели
С учетом равенства tg m sin m m по формуле (3.5) вычисляются углы дифракции, полученные значения заносим в таблицу 4.1 По формуле 1/m вычисляем обратные значения углов дифракции, полученные значения так же заносим в таблицу 4.1 Для построения первого графика воспользуемся методом наименьших квадратов - построение прямых по экспериментальным точкам. 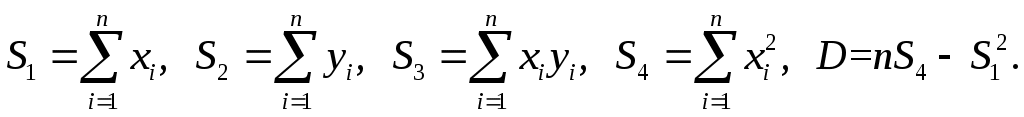 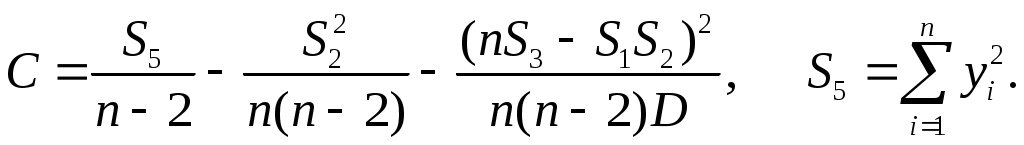    Угловой коэффициент первой прямой отрезок, отсекаемый первой прямой от оси OYАбсолютные погрешности вычисления параметров первой прямой   С учетом полученных параметров записывается уравнение первой прямой 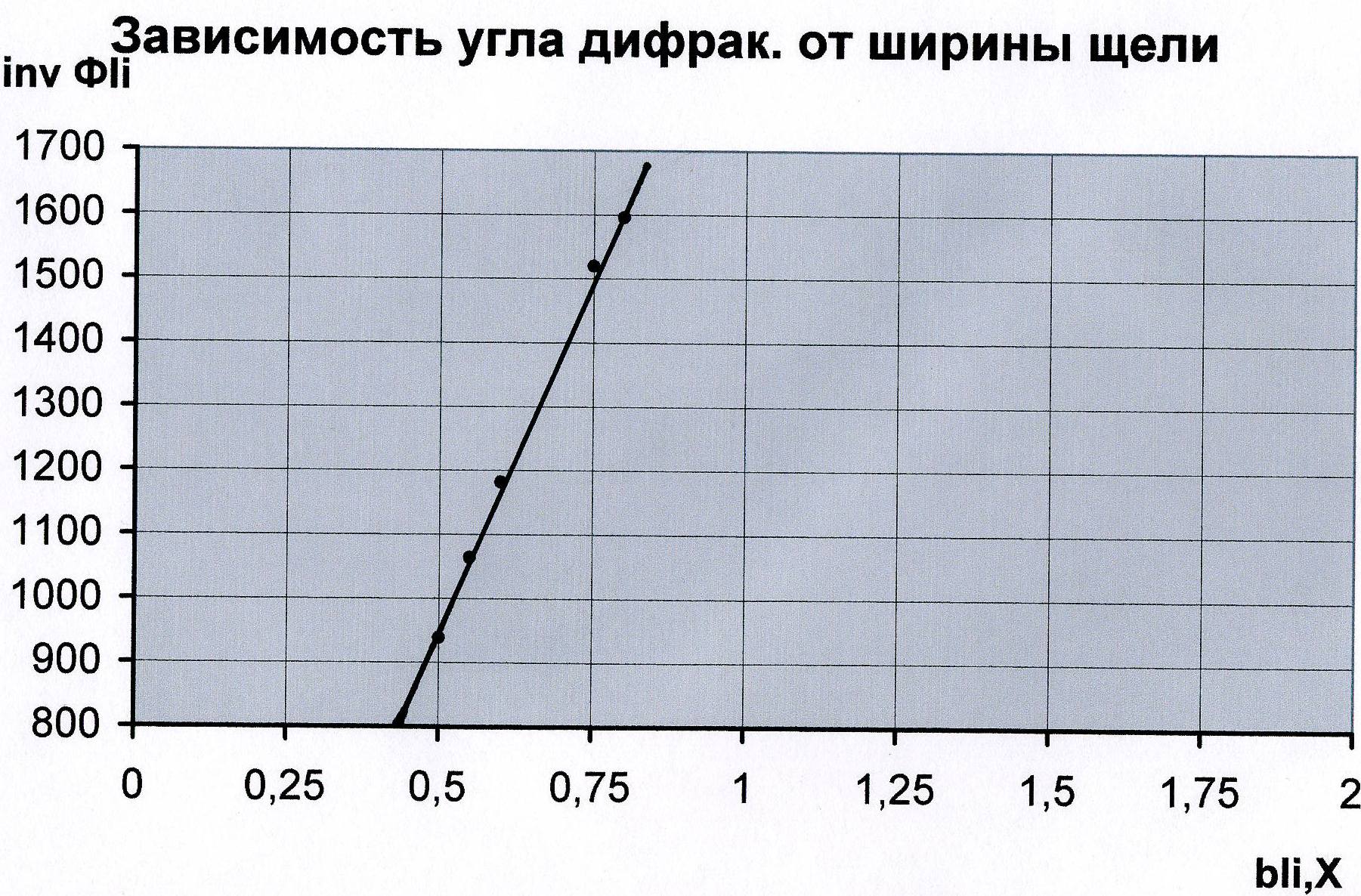   Рис 1 За систематическую погрешность  определения ширины щели можно принять максимальное из отклонений экспериментальных точек от прямой на оси b1. зависимость координат X от Y первой прямой  мС использованием вычисленного методом наименьших квадратов углового коэффициента прямой К1 определяется длинна волны излучения лазера.   мС учетом равенства tg m sin m m по формуле (3.5) вычисляются углы дифракции, полученные значения заносим в таблицу 4.2 4.2 Задание 2 Таблица 4.2 Данные для зависимости угла дифракции от номера минимума
Построение второго графика  угловой коэффициент второй прямой отрезок, отсекаемый второй прямой от оси OYАбсолютные погрешности вычисления параметров второй прямой   С учетом полученных параметров записывается уравнение второй прямой 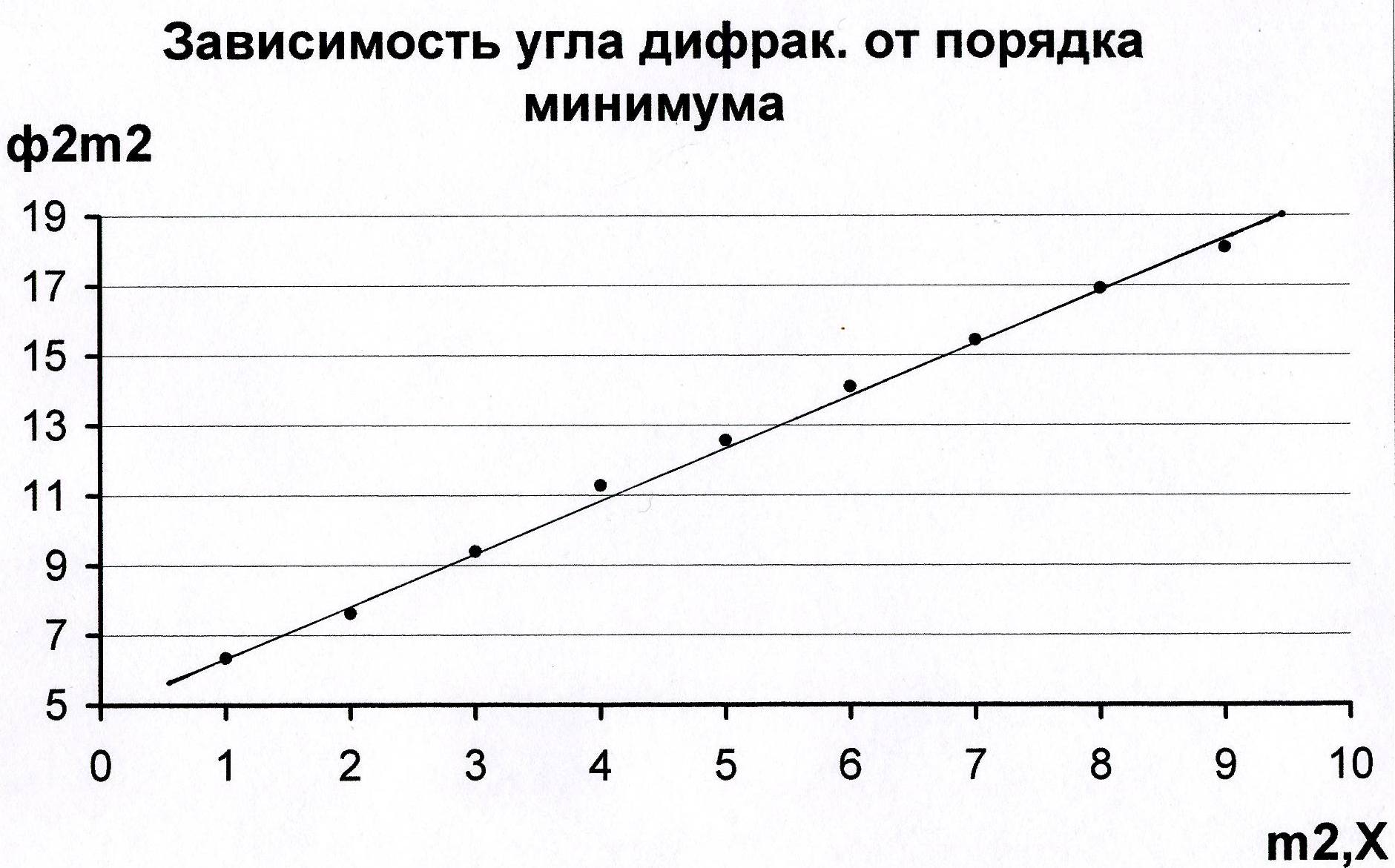  Рис 2 По формуле с использованием вычисленного методом наименьших квадратов углового коэффициента прямой К2 определяется ширина щели    мОтличие в процентах измеренного и вычисленного значений ширины щели   Абсолютная погрешность вычисления ширины щели дифракционным методом находится по формуле  Необходимая для вычисления относительная погрешность, зависит от относительных погрешностей, определения длинны волны лазера и углового коэффициента второй прямой  Погрешность  равна относительной погрешности  вычисления углового коэффициента первой прямой.Погрешность вычисляется по формуле        м5. ВЫВОДЫ Изучена дифракция Фраунгофера на щели. Определена, длинна волны лазерного излучения  . разница между вычисленным и табличным значениями составляет 23,2%. Рассчитаны размеры щелидифракционным методом  Отличие в процентах измеренного и вычисленного значений ширины щели составило 16,6 %. Построены графики отношения зависимости угла дифракции от ширины щели и угла дифракции от порядка минимума.6. ОТВЕТЫ НА КОНТРОЛЬНЫЕ ВОПРОСЫ 6.1 В чем заключается явление дифракции света? Дифракцией света называют совокупность явлений, которые обусловлены волновой природой света и наблюдаются при его распространении в среде с резко выраженными неоднородностями (например, при прохождении через отверстия в непрозрачных экранах, вблизи границ непрозрачных тел и т.д.) В более узком смысле под дифракцией понимают явление огибания светом малых препятствий, т.е. отклонения от законов геометрической оптики и следовательно проникновение света в область геометрической тени. 6.2Какие волны называются когерентными Для образования устойчивой интерференционной картины необходимо, чтобы источники волн имели одинаковую частоту, и разность фаз их колебания была постоянной. Источники, удовлетворяющие этому условию, называются когерентными. Волны таких источников также называются когерентными 6.3Какой тип дифракции – Френеля или Фраунгофера – реализуется в данном эксперименте и почему? В данной работе реализуется дифракция Фраунгофера – в параллельных лучах. 6.4Как изменится дифракционная картина, если гелий-неоновый лазер, излучающий красный свет, заменить кадмиевым лазером, излучающим, в синей области спектра? Изменится, длинна волны излучения лазера соответственно изменятся все параметры дифракционной картинки зависящие от этого. 6.5В чем заключается физический смысл понятия «зона Френеля»? Зоны Френеля, участки, на которые можно разбить поверхность световой волны для вычисления результатов дифракции света. В соответствии с принципом Гюйгенса щель можно рассматривать как совокупность новых источников, колеблющихся в одинаковых фазах. В качестве таких источников могут быть взяты зоны Френеля, которые в данном случае будут представлять собой полосы, параллельные краям щели. 6.6Что будет наблюдаться на экране (максимум или минимум интенсивности) в точке, для которой одновременно выполняются условия главных минимумов и главных максимумов? На экране будет наблюдаться максимум. 7. ПРИЛОЖЕНИЕ К работе прилагается регистрационный файл (*.REG). |
