Лабораторная работа № 2 Изучение дифракции лазерного излучения от щели. Отчет по ЛР№6. Лабораторная работа по курсу общей физики Изучение дифракции лазерного излучения от щели Проверил
 Скачать 0.73 Mb.
|
|
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР) Кафедра физики ОТЧЕТ Лабораторная работа по курсу общей физики Изучение дифракции лазерногоизлучения от щели Проверил Выполнили Преподаватель Студенты гр. 1В1 Бурнашов А.В. Абакунов А.В. Конюхов Е.С. 19 марта 2022 г. Шуцько Д.Д. 19 марта 2022 г. Томск 2022г. Введение Целью данной работы является изучение дифракции Фраунгофера на щели и определение размеров щели дифракционным методом. 1. Описание экспериментальной установки и методики измерений Дифракция света на щели исследуется на экспериментальной установке, схематично изображенной на рис. 1.1. 3  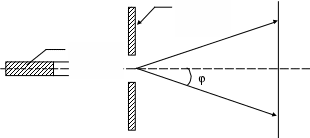 2 1 Рисунок 1.1 - Принципиальная схема наблюдения дифракции Фраунгофера с использованием в качестве источника света лазера 1 лазер; 2 щель; 3 экран с миллиметровой шкалой Методика эксперимента заключается в следующем: пучок когерентных параллельных лучей, испускаемых лазером 1, падает на щель 2. Регулируя щель микровинтом, можно ограничить фронт волны и вырезать лишь узкий плоский участок. В этом случае за щелью образуется поле вторичных волн, которые создают дифракционную картину, наблюдаемую на экране 3, отстоящем достаточно далеко от щели. 2. ОСНОВНЫЕ РАСЧЕТНЫЕ ФОРМУЛЫ Если на ширине щели при некотором угле φ уложится четное число зон Френеля, то при наложении все вторичные волны погасят друг друга. В соответствующем направлении, определяемом углом дифракции φ, интенсивность света будет равна нулю. Эти направления определяются соотношением bsin = ±2m /2, (3.1) где m = 1, 2, 3, 4 – порядок минимума. Если на ширине щели при некотором угле уложится нечетное число зон Френеля, то в этом направлении будет наблюдаться максимум света. Условие максимума дается соотношением bsin = ± (2m + 1) /2, (3.2) где m = 1, 2, 3, 4 – порядок максимума. Интенсивность максимумов уменьшается по закону  (3.3)где  Вычисление углов дифракции φm, tg φm = (2xm)/(2l), (3.5) где 2xm – расстояние между центрами темных полосок, l – расстояние от щели до экрана. Поскольку углы дифракции малы, можно считать верным равенство tg φm ≈ sin φm ≈ φm. (3.6) Длина волны λ можно определяется, если использовать метод наименьших квадратов для проведения прямой 1/φ = f(b). В этом случае λ определяется через угловой коэффициент прямой. 3. РЕЗУЛЬТАТЫ РАБОТЫ И ИХ АНАЛИЗ 4.1 Задание 1 Таблица 4.1 Данные для зависимости угла дифракции от ширины щели
С учетом равенства tg m sin m m по формуле (3.5) вычисляются углы дифракции, полученные значения заносим в таблицу 4.1 По формуле 1/m вычисляем обратные значения углов дифракции, полученные значения так же заносим в таблицу 4.1 Для построения первого графика воспользуемся методом наименьших квадратов - построение прямых по экспериментальным точкам. 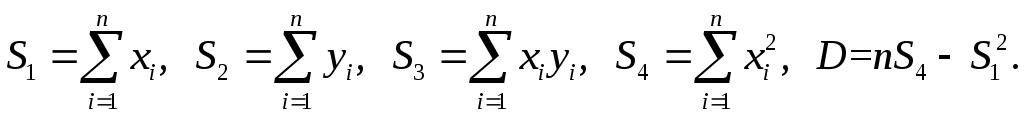 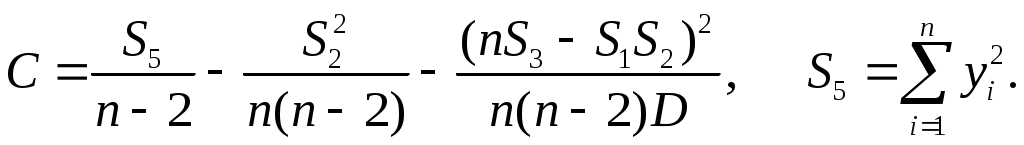    Угловой коэффициент первой прямой отрезок, отсекаемый первой прямой от оси OYАбсолютные погрешности вычисления параметров первой прямой   С учетом полученных параметров записывается уравнение первой прямой 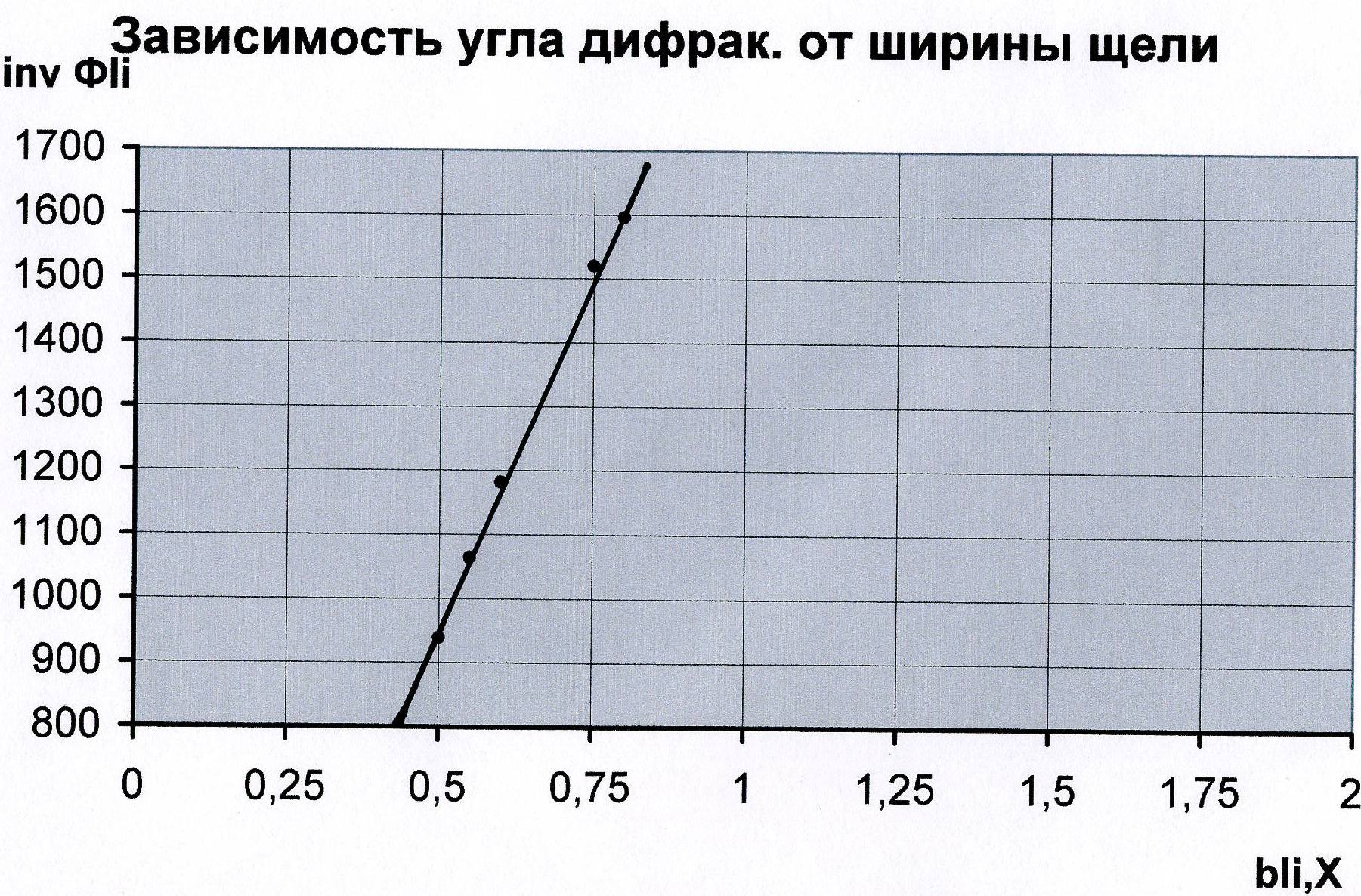   Рис 1 За систематическую погрешность  определения ширины щели можно принять максимальное из отклонений экспериментальных точек от прямой на оси b1. зависимость координат X от Y первой прямой  мС использованием вычисленного методом наименьших квадратов углового коэффициента прямой К1 определяется длинна волны излучения лазера.   мС учетом равенства tg m sin m m по формуле (3.5) вычисляются углы дифракции, полученные значения заносим в таблицу 4.2 4.2 Задание 2 Таблица 4.2 Данные для зависимости угла дифракции от номера минимума
Построение второго графика  угловой коэффициент второй прямой отрезок, отсекаемый второй прямой от оси OYАбсолютные погрешности вычисления параметров второй прямой   С учетом полученных параметров записывается уравнение второй прямой 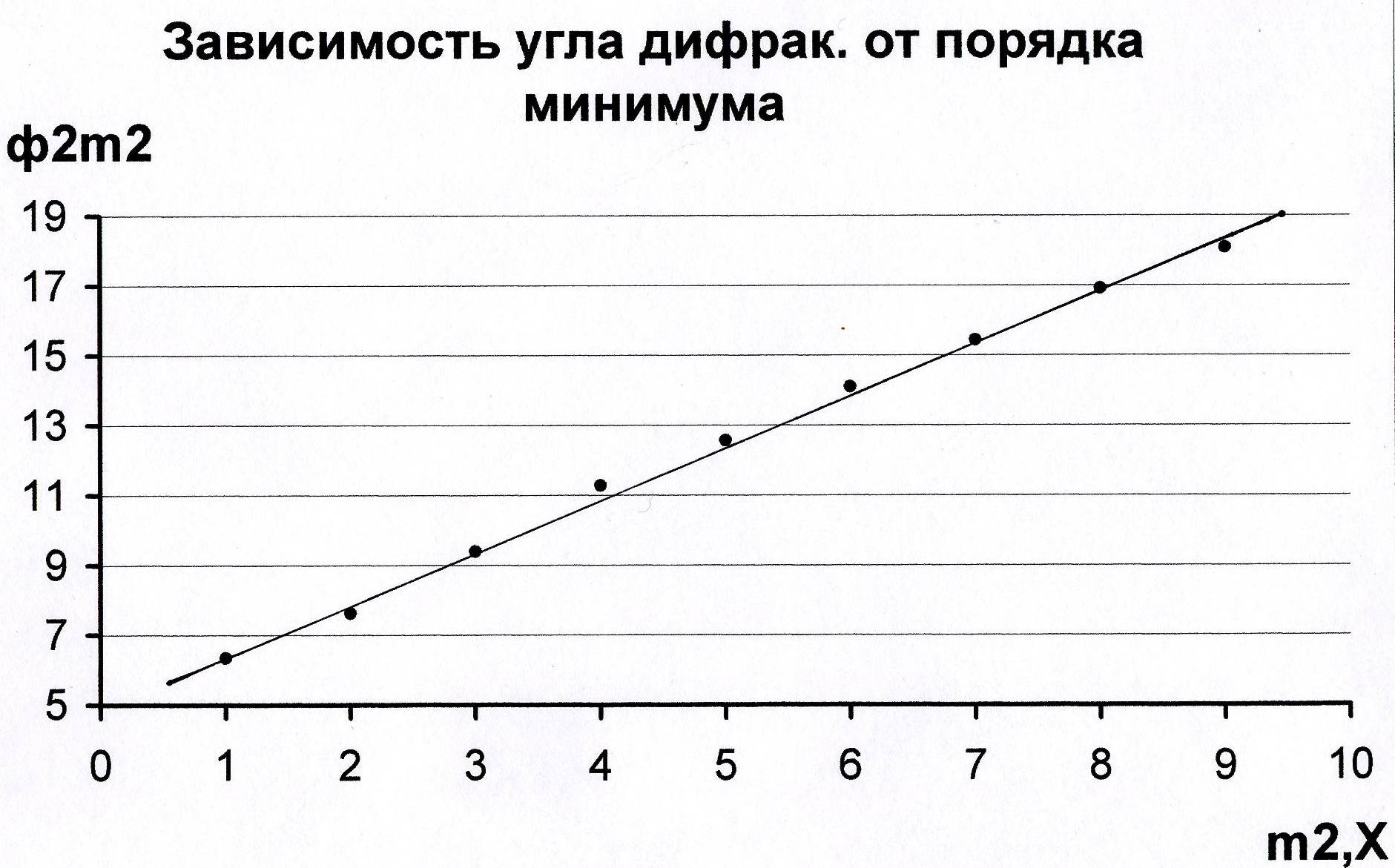  Рис 2 По формуле с использованием вычисленного методом наименьших квадратов углового коэффициента прямой К2 определяется ширина щели    мОтличие в процентах измеренного и вычисленного значений ширины щели   Абсолютная погрешность вычисления ширины щели дифракционным методом находится по формуле  Необходимая для вычисления относительная погрешность, зависит от относительных погрешностей, определения длинны волны лазера и углового коэффициента второй прямой  Погрешность  равна относительной погрешности  вычисления углового коэффициента первой прямой.Погрешность вычисляется по формуле        мЗаключение Изучена дифракция Фраунгофера на щели. Определена, длинна волны лазерного излучения  . разница между вычисленным и табличным значениями составляет 23,2%. Рассчитаны размеры щели дифракционным методом  . Отличие в процентах измеренного и вычисленного значений ширины щели составило 16,6 %. Построены графики отношения зависимости угла дифракции от ширины щели и угла дифракции от порядка минимума. |
