Дифракция микрочастиц на щели
 Скачать 0.58 Mb. Скачать 0.58 Mb.
|
|
МИНОБРНАУКИ РОССИИ Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И. Ульянова (Ленина) Кафедра МИТ отчет по лабораторной работе №3 по дисциплине «Физические основы микро- и наноэлектронике» Тема: Дифракция микрочастиц на щели
Санкт-Петербург 2020 Цель работы: наблюдение вероятностного распределения микрочастиц после прохождения через щель, настраивая параметры количества свободных частиц проходящего через щель, количества анимированных частиц и скорости анимации для построения модели дифракции микрочастиц. Основные понятия и определения В 1923 г. французский физик Лу и де Бройль высказал гипотезу, согласно которой корпускулярно - волновой дуализм является универсальным свойством любых материальных объектов, а не только света. Фотон — не единственная элементарная частица в микромире. Любая микрочастица обладает, помимо корпускулярных, еще волновыми свойствами. Это значит, что частица массой m, движущаяся со скоростью υ, характеризуется не только координатами, импульсом р и энергией Е, но и подобно фотону частотой ν и длиной волны λ: 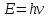 (1) (1) Любой частице, обладающей импульсом р, соответствует длина волны де Бройля: 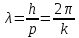 (2) (2) где λ - длина волны, м; h - постоянная Планка; Дж·c; р - импульс, кг·м/с; κ - волновой вектор, рад· 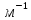 . . Наличие волновых свойств у микрочастиц означает, что можно наблюдать их интерференцию и дифракцию. Подтвержденная на опыте идея де Бройля о двойственной природе микрочастиц — корпускулярно - волновом дуализме — принципиально изменила представление об облике микромира. Поскольку всем микрообъектам присущи и корпускулярные и волновые свойства, то, очевидно, любую из этих «частиц» нельзя считать ни частицей, ни волной в классическом понимании. Возникла потребность в такой теории, в которой волновые и корпускулярные свойства материи выступали бы не как исключающие, а как взаимно дополняющие друг друга. В основу такой теории — волновой, или квантовой, механики и легла концепция де Бройля. Это отражается даже в названии волновая функция для величины, описывающей в этой теории состояние системы. Квадрат модуля волновой функции определяет вероятность состояния системы, и поэтому о волне де Бройля говорят как о волнах вероятности (точнее, амплитуд вероятности). Для свободной частицы с точно заданным импульсом, движущейся вдоль оси х, волновая функция имеет вид: 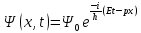 (3) (3)Квадрат модуля волновой функции | 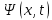 |² определяет вероятность нахождения частицы в момент времени t в точке с координатой х. Волновая функция является функцией координат и времени и может быть найдена путем решения уравнения: |² определяет вероятность нахождения частицы в момент времени t в точке с координатой х. Волновая функция является функцией координат и времени и может быть найдена путем решения уравнения: 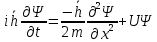 (4) (4)где і - мнимая единица; 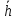 = h/2π - редуцированная постоянная Планка (постоянная Дирака); = h/2π - редуцированная постоянная Планка (постоянная Дирака); 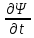 − производная по времени t; − производная по времени t; m — масса частицы; 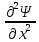 − вторая производная по координате x; − вторая производная по координате x; 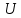 – потенциальная энергия частицы, Дж; – потенциальная энергия частицы, Дж; 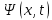 − волновая функция. − волновая функция. Это нерелятивистское волновое уравнение Шредингера для одномерного случая. Уравнение Шредингера не выводится, а вводится как новый принцип, или постулат, и затем следствия из него проверяются на эксперименте. Необходимые требования к уравнению Шредингера: 1. Уравнение должно быть линейным, т.к. должен выполняться принцип суперпозиции. 2. Уравнение должно содержать только фундаментальные константы в качестве коэффициентов, например, такие константы как e, m, ћ. 3. В уравнение не должны явно входить параметры движения, например, координата или скорость υ. Итак, уравнение Шредингера - основное динамическое уравнение нерелятивистской волновой механики, играет такую же важную роль, как уравнения Ньютона в классической механике и уравнения Максвелла в теории электромагнитного поля. Релятивистское уравнения для волновой функции является уравнение Клейна-Гордона, то есть удовлетворяющее требованиям относительности теории уравнение для частиц со спином нуль. Для свободной частицы уравнение Клейна – Гордона записывается в виде: 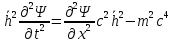 (1.5) (1.5)где 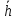 = h/2π - редуцированная постоянная Планка (постоянная Дирака); = h/2π - редуцированная постоянная Планка (постоянная Дирака); 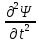 −вторая производная по времени t; −вторая производная по времени t; 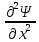 −вторая производная по координате x; −вторая производная по координате x; с — скорость света в вакууме, м/c; m — масса частицы; 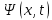 − волновая функция. − волновая функция.Решением уравнения является функция 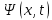 , зависящая только от координаты х и времени t. Следовательно, частицы, описываемые этой функцией, не обладают никакими дополнительными внутренними степенями свободы, т. е. действительно являются бесспиновыми. , зависящая только от координаты х и времени t. Следовательно, частицы, описываемые этой функцией, не обладают никакими дополнительными внутренними степенями свободы, т. е. действительно являются бесспиновыми. 1.2. Дифракция фотонов Дифракцией называется совокупность явлений, наблюдаемых при распространении света в среде с резкими неоднородностями (например, вблизи границ непрозрачных тел, сквозь малые отверстия и т.п.) и связанных с отклонениями от законов геометрической оптики. В частности, дифракция приводит к огибанию световыми волнами препятствий и проникновению света в область геометрической тени. Явление дифракции заключается в перераспределении светового потока в результате суперпозиции волн, возбуждаемых когерентными источниками, расположенными непрерывно. Распространение света в виде потока фотонов и квантовый характер взаимодействия света с веществом подтверждены в многочисленных экспериментах. Казалось бы, это является убедительным доказательством квантовых представлений о свойствах света. Однако целый ряд оптических явлений (поляризация, интерференция, дифракция) неопровержимо свидетельствуют о волновых свойствах света. Прямым подтверждением этого явились опыты 1909 г. Джофри Тейлора по наблюдению дифракции поочередно летящих одиночных фотонов. Для этого интенсивность света, падающего на щель, следовало существенно понизить (например, как в экспериментах Тейлора - с помощью светофильтров). Ослабление интенсивности означает уменьшения числа Nф падающих на щель фотонов. В результате можно на столько уменьшить Nф, что фотоны будут следовать друг за другом с интервалом времени, на несколько порядков превышающим время, за которое фотон попадает на фотопластинку ФП, помещенную за щелью на расстоянии L. На рисунке 1 показан опыт по дифракции одиночных фотонов на щели. 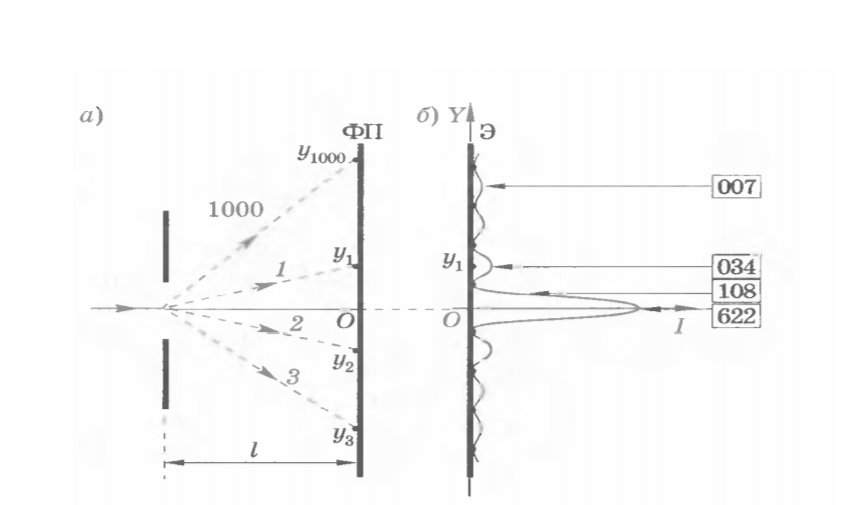 Рисунок 1.1 - Дифракция одиночных фотонов на щели: а) попадание на фотопластинку одиночного фотона; б) суммирование результатов отдельных измерений Благодаря этому фотоны не могут взаимодействовать (интерферировать) друг с другом, а налетают на щель поодиночке. Первый фотон, пройдя щель, попадает на фотопластинку в точку с координатой y1. Затем на фотопластинку попадает второй фото в точку с координатой y2 и т. д. На рисунке 1.1,а показаны возможные точки попадания фотонов на фотопластинку. Результат суммирования числа фотонов, попадающих в окрестность точки с определенной координатой у, приведен на рисунке 1.1,б (после 1000 экспериментов). Например, в окрестность точки с координатой у1 попали 34 фотона. Чем больше фотонов попадают в данную область, тем больше интенсивность света в ней. Полученная зависимость интенсивности света от координаты полностью совпадает с картиной распределения интенсивности света за щелью, описываемой волновой теорией. Дифракционная картина на экране Э за щелью оказывается результатом статистического распределения отдельных фотонов на экране. В область дифракционных максимумов попадает много фотонов, в области минимумов их мало. Анализ дифракции одиночных фотонов на щели показывает, что движение фотонов принципиально отличается от движения классической частицы (материальной точки) в каждом отдельном случае можно однозначно предсказать, зная начальную координату частицы и ее скорость. Однако заранее невозможно установить, в какую точку после дифракции на щели попадет фотон. Можно говорить лишь о вероятности попадания фотона в окрестность определенной точки. 1.3. Волновая редукция Волновая функция непрерывно изменяется во времени. Этот процесс полностью описывается волновым уравнением Шредингера. При взаимодействии квантового объекта с классическим происходит редукция. Этот процесс носит случайный характер, и он не описывается волновым уравнением. В этом случае волновое уравнение позволяет только рассчитать вероятность тех или иных возможных скачкообразных изменений в волновой функции. И если взаимодействие произошло, то волновую функцию следует зачеркнуть и написать новую, с учётом произошедших изменений. Таким образом, редукция волновой функции – это мгновенное и скачкообразное изменение волновой функции, которое не описывается волновым уравнением Шредингера. Обработка результатов измерений  В ходе эксперимента было проведено 4 опыта, два опыта с количество частиц Q = 50, два опыта с количеством частиц Q = 300. Опыт №1.1: Количество частиц Q = 300 Частицы были распределены на 5 уровней со значениями: 1) 34 2) 59 3) 113 4) 63 5) 31 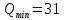 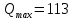 Опыт №1.2: Количество частиц Q = 300 Частицы были распределены на 5 уровней со значениями: 1) 29 2) 67 3) 117 4) 51 5) 36 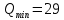 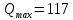 Опыт №2.1: Количество частиц Q = 50 Частицы были распределены на 5 уровней со значениями: 1) 8 2) 9 3) 19 4) 10 5) 4 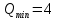 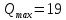 Опыт №2.2: Количество частиц Q = 50 Частицы были распределены на 5 уровней со значениями: 1) 4 2) 10 3) 18 4) 11 5) 7 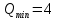 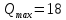 Вывод: в ходе выполнения данной работы были получены результаты, по которым можно сделать вывод, что движение фотона предугадать невозможно. Можно лишь рассчитать вероятность его нахождения в какой-либо точке. Для доказательства было проведено 4 опыта, в каждом из которых было своё уникальное распределение частиц. Причём несмотря на то, что в парных опытах общее количество фотонов было одинаковым. |
