КР №1, В7. Решение Экстремальное значение скорости частицы наибольшее возможное ее значение. Исследуем v'(t) а) V'(t)A2Bt

Название	Решение Экстремальное значение скорости частицы наибольшее возможное ее значение. Исследуем v'(t) а) V'(t)A2Bt
Дата	03.01.2023
Размер	47.44 Kb.
Формат файла
Имя файла	КР №1, В7.docx
Тип	Решение #871205

107. Скорость прямолинейно движущейся частицы изменяется по закону

, где А = 12 м/с и

. Найти: а) экстремальное значение скорости частицы; б) координату х частицы для этого же момента времени, если в момент t = 0,

Дано:
А = 12 м/с
В = 2 м/с²
Найти:
а) Vmax, б) x(t)
Решение:
Экстремальное значение скорости частицы – наибольшее возможное ее значение.
Исследуем v'(t)

а) V'(t)=A-2Bt

V'(t)=0 при t=A/(2B)

Vmax=A²/(2B)-A²/(4B)=A²/(4B)=12²/(4*2)=144/8=18 м/с

б) x(t)=ʃ(V(t)dt)

x(t)=At²/2+Bt³/3+C

константу C найдем из начальных условий

x(A/2B)=A³/(8B²)-A³/(24B²)=A³/(12B²)

x(A/2B)=12³/(12*2²)=1728/48=36 м
Ответ: а) Vmax =18 м/с, б) x(A/2B) = 36 м.

117. Ледяная гора составляет с горизонтом угол 30. Из некоторой точки по ней снизу вверх движется тело с начальной скоростью 10 м/с. Коэффициент трения скольжения 0,1. Определите скорость тела при его возвращении в ту же точку.
Дано:
α=30

μ=0.1
Vo=10м/с
Найти:
U-?
Решение:
m*Vo²/2=m*g*h-μ*m*g*cosα*L (L - длина горки)
L=h/sinα
Vo²/2=g*h*(1-μ/tgα)
h=Vo²*(1-μ/tgα)/(2*g) =100*(1-0.1/0.58) / (2*10) ≈ 4.14 м
L=4.14/0.5=8.28 м
m*U²/2=m*g*h-μ*m*g*cosα*L
U=√(2*g*(h-μ*L*cosα)) = √(2*10*(4.14-0.1*8.28*0.87)) ≈ 8.27 м/с
Ответ: U ≈ 8.27 м/с.

127. Человек массой 60 кг, бегущий со скоростью 8 км/ч, догоняет тележку массой 80 кг, движущуюся со скоростью 2,9 км/ч и вскакивает на нее. С какой скоростью будет двигаться тележка? С какой скоростью будет двигаться тележка, если человек бежал ей навстречу?
Дано:
m1 = 60 кг

v1 = 8 км/ч = 2,(2) м/с
m2 = 80 кг
v2 = 2,9 км/ч = 0,806 м/с
Найти:

u -? u' -?
Решение:
а)

Проекция на ось x:

Скорость тележки с человеком

б)

Проекция на ось x:

Скорость тележки с человеком

Ответ: u=1.41 м/с = 5.076 км/ч, u'= -0.49м/с = -1.764 км/ч

137. Груз, положенный на чашу весов, сжимает пружину на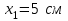

. Найти величину сжатия пружины для случая, когда этот же груз падает на чашку весов с высоты h = 10 см.
Дано:
х1 = 5 см
h = 10 см
Найти:
х2 -?
Решение:
x1 = mg/k = k = mg/x1, где k - коэффициент упругости пружины

По закону сохранения энергии:

mg(h + x2) = k*(x2^2)/2. Или h + x2 = (x2^2)/(2*x1)

x2 = x1 + √[(x1)² + 2(x1)h] = 16.18 см.
Ответ: х2 = 16.18 см.

147. Блок, имеющий форму диска массой 0,4 кг, вращается под действием силы натяжения нити, к концам которой подвешены грузы массами 0,3 кг
и 0,7 кг. Определить силы натяжения нити по обе стороны блока.
Дано:
m1 = 0.3 кг
m2 = 0.7 кг
m = 0.4 кг
Найти:

Т1-?, Т2-?
Решение:
По II закону Ньютона:

T1-m1*g= m1*a (1)

T2-m2*g=-m2*a (2) , где а – ускорение грузов
T2*R-T1*R=J*E, где J - момент инерции блока относительно оси вращения

Е – угловое ускорение
Если нить не проскальзывает, то
Е=a/R => учитывая, что J=mR²/2, получим:
(Т2-Т1)*R=mR²/2*a/R

T2-T1=(m/2)*a

a=2*(T2-T1)/m

Подставляем в (1) и (2):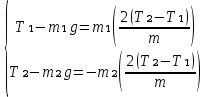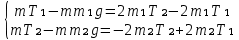

T1=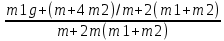

=3.92Н

T2=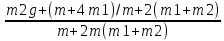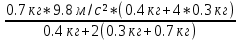

=4.57Н

Ответ: Т1=3.92Н, Т2=4.57Н.

157. Карандаш, поставленный вертикально, падает на стол. Длина карандаша l= 15 см. Найти угловую и линейную скорости середины карандаша в конце падения.
Дано:
l= 15 см = 0.15м
Найти:
ϖ - ? v - ?
Решение:

Центр тяжести карандаша первоначально находится на высоте h и имеет потенциальную энергию