Имитационная модель системы массового обслуживания. Лабораторная работа Имитационная модель системы массового обслуживания
 Скачать 179 Kb.
|
|
Лабораторная работа «Имитационная модель системы массового обслуживания» Данная лабораторная работа состоит в разработке компьютерной программы имитационной модели системы массового обслуживания (СМО) и расчетах характеристик этой системы на основе работы этой программы. Дадим вначале краткое описание СМО. Примерами систем массового обслуживания являются бытовые системы типа ремонтных мастерских или системы общего пользования типа авиа и железнодорожных касс и т. д. Такие системы структурно включают в себя приемные устройства, устройства исполнения заказов (исполнительные устройства) и устройства выдачи готовых изделий. Важнейшими характеристиками СМО являются количество исполнительных устройств «n» и законы потоков поступления заявок и исполнения заявок.. Принципиальная схема СМО представлена на Рис. 1. Поток заявок, а также время исполнения заявок, как правило, являются случайными величинами. Законы распределения этих случайных величин могут быть самыми различными. Если законы распределения потока заявок и потока исполнения заявок удовлетворяют некоторым определенным предположениям, то такие СМО будем называть классическими и для них получены аналитические соотношения для вычисления основных характеристик СМО. Если же законы распределения потока заявок или потока исполнения заявок не удовлетворяют этим предположениям, то необходимо посредством практических измерений этих величин и последующей статистической обработки получить приближенные выражения для их законов распределения, а затем методами имитационного моделирования исследовать подобные СМО на компьютере. Наибольшее распространение на практике получили СМО с очередью и СМО с отказами. Для СМО с очередью заявка, поступившая в систему и заставшая все «n» устройств занятыми обработкой ранее поступивших заявок, становится в очередь. Для таких СМО важнейшими характеристиками системы являются вероятность отсутствия очереди и длина очереди. Для СМО с отказами заявка, поступившая в систему и заставшая все «n» устройств исполнения занятыми, получает отказ. Для таких СМО важнейшей характеристикой системы является вероятность отказа. 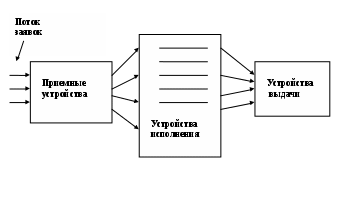 Рис. 1. Применение метода имитационного моделирования к системам массового обслуживания состоит в моделировании процесса поступления заявок в систему, моделировании процесса обслуживания, накопления результатов и обработки результатов для получения содержательных выводов о характеристиках системы (среднего числа заявок в очереди, среднего числа занятых устройств, вероятности отказа и т. д.). Реализация имитационных моделей в настоящее время осуществляется главным образом на компьютерах и с помощью математических пакетов программ, установленных на этих компьютерах. Для более четкого и ясного представления о характере имитационных моделей систем массового обслуживания, а также для того, чтобы иметь возможность обсуждать проблемы, связанные с имитационным моделированием таких систем, рассмотрим простейшую систему массового обслуживания с отказами с n обслуживающих устройств и со случайными моментами поступления заявок и случайными временами обслуживания заявок. Блок-схема алгоритма такой модели представлена на Рис. 2. 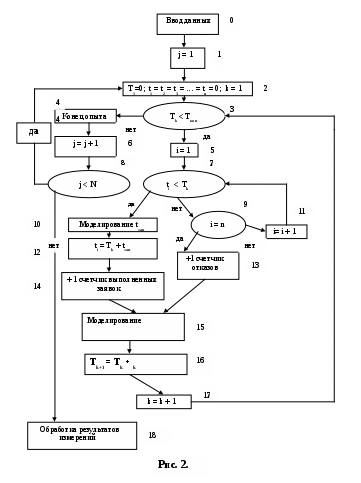 Здесь введены следующие обозначения: tj – время освобождения j-го устройства от обслуживания; tзан – время занятости устройства обслуживанием (случайная величина); Tk– время поступления k-й заявки; Ткон – время окончания опыта; τk– интервал времени между двумя соседними заявками (случайная величина); N – общее число опытов, например, рабочих дней и т. д.; j – индекс номера опыта; k – индекс номера заявки; i – индекс номера обслуживающего устройства; n – общее число обслуживающих устройств. Система не предусматривает очереди, и заявки, заставшие все устройства обслуживания занятыми, получают отказ. Для определения приближенных значений характеристик системы в модели предусмотрен подсчет числа выполненных заявок и числа заявок, получивших отказ. Рассмотрим теперь работу алгоритма. В блоке 1(номера блоков указаны цифрами справа, сверху, реже слева от блока) задается номер опыта (например, номер рабочего дня). В блоке 2 задаются начальные условия каждого опыта: первая заявка поступает в момент 0: Т1 = 0; все устройства обслуживания свободны: t1= t2=…= tn=0; первая заявка имеет номер 1: k=1. В блоке 3 проверяется условие, попала ли заявка со временем прихода Tk в рамки окончания опыта, т. е. условие Tk<Tкон. Если попала, то в блоке 5 начинается проверка занятости устройств обслуживания; если не попала, то в блоке 4 организуется процедура завершения опыта. В блоке 7 осуществляется проверка условия, свободно ли i-е устройство обслуживания к моменту поступления k-й заявки Tk. Если i-е устройство обслуживания свободно, то заявка поступает на обслуживание: в блоке 10 моделируется случайное время занятости устройства tз, затем в блоке 12 формируется новое время освобождения i-го устройства от обслуживания: ti =Tk+ tз и в блоке 14 к счетчику числа выполненных заявок добавляется единица. Таким образом, либо в блоке 13, либо в блоке 14 завершается присутствие k-й заявки в СМО: заявка либо будет обслужена, либо получит отказ, и необходимо приступить к рассмотрению следующей заявки. В блоке 15 моделируется случайное значение интервала времени τk между двумя очередными заявками; в блоке 16 формируется новое значение времени поступления очередной заявки: Tk+1= Tk+ τk, а в блоке 17 – номер новой заявки и управление передается блоку 3 для рассмотрения этой заявки. Рассмотрим теперь процедуру завершения моделирования. В блоке 6 увеличивается на единицу номер опыта (например, номер рабочего дня), а в блоке 8 проверяется условие, является ли этот опыт последним: если опыты еще не завершены («да» в блоке 8), то очередной опыт моделируется (управление передается блоку 2), если же опыты завершены («нет» в блоке 8), то далее в блоке 18 осуществляется обработка результатов эксперимента. Под обработкой результатов моделирования понимается получение приближённых значений характеристик СМО. Например, в рассмотренной здесь модели нетрудно получить следующие характеристики СМО с отказами: - среднее число обслуженных заявок как среднее арифметическое выполненных заявок, накопленных в счетчике заявок, по всем N опытам; - среднее число отказов как среднее арифметическое отказов, накопленных в счетчике отказов, по всем N опытам; - вероятность отказа как среднее арифметическое отношений числа отказов ко всем заявкам, поступившим в систему (сумма значений двух вышеуказанных счетчиков), по всем N опытам. Аналогичную блок-схему можно предложить для СМО с очередью. Особенностью и достоинством имитационных моделей СМО по сравнению с аналитическими методами, рассмотренными в предыдущей главе, является то, что в них могут быть рассмотрены СМО с любыми законами распределения времен поступления заявок и любыми законами времен обслуживания, достаточно лишь смоделировать эти величины в соответствии с их законами в блоках 10, 12, 15, 16. На практике, для получения этих законов необходимо организовывать статистическое экспериментирование для получения значений величин времен поступления заявок и времен обслуживания («хронометраж»). Недостатком имитационных моделей является то, что они могут быть реализованы лишь при конкретных числовых значениях всех величин, входящих в моделируемую систему, и для исследования моделей с меняющимися в некотором диапазоне параметрами (например, число устройств обслуживания n) необходимо достаточно объемное по времени моделирование. В рассмотренном алгоритме поток заявок характеризуется случайной величиной  - интервал времени между двумя последовательными заявками (эта величина моделируется в блоке 15 и она имеет различные законы распределения для различных вариантов задания лабораторной работы). Поток исполнения заявок характеризуется здесь случайной величиной tзан - время занятости линии обслуживанием заявки (эта величина моделируется в блоке 10 и она также имеет различные законы распределения для различных вариантов задания).Переходим к самому заданию по лабораторной работе. Задание 1) Для всех вариантов работы составить программу функционирования модели СМО с отказами в соответствии с вышерассмотренным алгоритмом. Для всех вариантов: число опытов N (число рабочих дней, например) взять равным N = 200, продолжительность опыта Tкон (продолжительность рабочего дня) взять равным Tкон = 8 часов = 480 минут, число линий обслуживания (число занятых обслуживанием устройств) «n» взять равным n = 5. В соответствии с номером варианта и данными таблицы 1, запрограммировать моделирование случайных величин и tзан в блоках 15 и 10 по их плотностям вероятности f1( ) и f2(t) из таблицы 1.Таблица 1.
Запрограммировать накопление числа выполненных заявок и числа отказов в соответствующих счетчиках. После «проигрывания» модели 200 раз запрограммировать вычисление и вывод на печать (на экран) следующих характеристик СМО с отказами: - среднее число выполненных заявок и оценку вероятности выполнения заявки; - среднее число отказов и оценку вероятности отказа. 2) Аналогично предыдущему разработать модель СМО с очередью с теми же исходными данными, что и в предыдущем разделе и с помощью этой модели получить следующие характеристики: - среднюю длину очереди; - оценку вероятности отсутствия очереди; - оценку вероятности того, что все устройства обслуживания будут заняты. |
0
0
e -
, 0
, 0
2 , 0
, 0
2 , 
e-x/3, 
0