Лабораторная работа Индуктивно-связанные цепи (ЭиЭ) БиМАС. Лабораторная работа Индуктивно связанные цепи
 Скачать 233.78 Kb. Скачать 233.78 Kb.
|
|
Лабораторная работа «Индуктивно - связанные цепи» Цель работы: Изучение явлений и экспериментальное определение параметров элементов в индуктивно-связанных электрических цепях. Краткие теоретические сведения. Магнитный поток обусловлен током Ф = WI/ Rмаг На рис.1. показаны магнитные потоки индуктивно-связанных катушек: Ф21 и Ф12 – потоки взаимной индукции; Фд - поток рассеяния. Полный магнитный поток, создаваемый током каждой катушки, состоит из потока рассеяния и потока взаимной индукции и называется потоком самоиндукции: Ф11 = ФS1 + Ф21 - для первой катушки, Ф22 = ФS2 + Ф12 - для второй катушки. Эти потоки определяют величины собственных индуктивностей L1 , и L2 катушек. Р 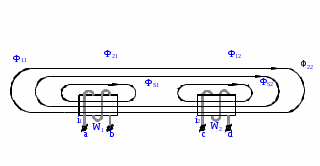 ис.1. Связь потокосцепления взаимной индукции одной электрической цепи током другой характеризуется взаимной индуктивностью М. Если потокосцепление 12 первой катушки обусловлено током i2 второй катушки, то взаимная индуктивность равна: 12 W1Ф12 М12 = ------- = ---------- (1) i2 i2 Аналогично для второй катушки: 21 W2Ф21 М21 = ------- = ---------- (2) i1 i1 Для линейных электрических цепей взаимная индуктивность М12 = М21 = М и зависит от геометрических размеров, числа витков и взаимного расположения катушек. Э.д.с. взаимной индуктивности: d21 di1 e2M = ------- = - M ------- dtdt d12 di2 e1M = ------- = - M ------- dtdt При синусоидальном изменении токов действующие значения э.д.с. взаимной индукции: . . . E2M = -jMI1 = -j xM I1 . . . (3) E1M = -jMI2 = -j xM I2 Полное потокосцепление каждого элемента: 1 = 11 + 12 = W1 Ф1 + W1 Ф12 = L1i1 + Mi2 2 = 22 + 21 = W2 Ф2 + W2 Ф21 = L2i2 + Mi1 (4) Степень индуктивной связи двух элементов характеризуется коэффициентом связи: 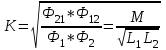 (5) (5)Если протекающий по катушкам ток изменяется во времени, то напряжения на катушках: d1 u1 = r1i + ------- dt d1 u1 = r1i + ------- (6) 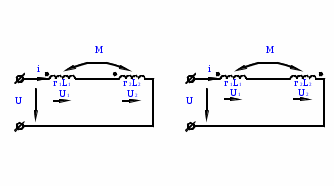 а) - согласное включение б) - встречное включение Рис. 2. При синусоидально изменяющемся токе уравнения (6) можно записать так: . . . . U1 = r1I + j(L1M)I = (r1 j x1Э)I . . . . U2 = r2I + j(L2M)I = (r2 j x2Э)I (7) . . . . . . . U = U1 + U2 = (r1 + r2)I + j(L1 + L2+2M)I = (rЭ+ j xЭ)I = ZЭI Где - rЭ = r1 + r2 ; x1Э= (L1 M); x2Э= (L2 M); xЭ= (L1 + L2 2M) Входное комплексное сопротивление цепи: 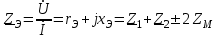 где - 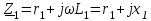 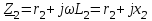 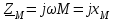 При согласном включении параллельно соединенных индуктивно-связанных катушек (рис. 7.3) уравнения состояния цепи имеют вид: . . . . U1 = r1I1 + jL1 I1 + jMI2 = 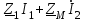 . . . . U2 = r2I2 + jL2 I2 + jMI1 = 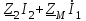 . . . I = I1 + I2 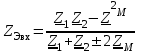 (8) (8)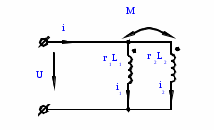 Рис. 3. Комплексные значения полных мощностей в катушках при согласном включении: 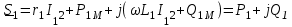 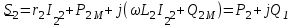 где - P1M = MI1I2 sin(1 - 2); (9) P2M = -MI1I2 sin(1 - 2); (10) Q1M = Q2M = MI1I2cos(1 - 2); При согласном соединении (М > 0) и при (1 - 2) из уравнения (10) получаем P1M > 0, P2M < 0, т.е. в первую катушку поступает мощность 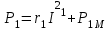 , , которая больше мощности, расходуемой в первой катушке на тепловые потери на величину мощности P1M , передаваемой из первой катушки во вторую. Во вторую катушку сеть поставляет мощность на величину P2M меньшую, чем мощность тепловых потерь во второй катушке 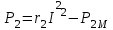 При встречном соединении (М < 0) и 1 - 2/2 P1M < 0, а P2M > 0 - мощность передается из второй катушки в первую. Экспериментальное определение взаимной индуктивности М можно произвести двумя способами: по величине э.д.с. взаимоиндукции (рис.4): E1M E2M М = ------ илиМ = ------. I2 I1 по величине реактивного сопротивления цепи при последовательном соединении катушек в случае встречного и согласного включения: 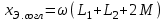 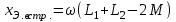 xЭ. cогл. - xЭ. встр. тогдаxM = M = --------------------- 4 xЭ. cогл. - xЭ. встр. M = ---------------------- 4 Вольтметр должен иметь большое входное сопротивление. Порядок выполнения и содержание отчета. 1. По схеме рис.5. собрать электрическую цепь. Измерить ток, напряжение и мощность для каждой катушки, установив заданное напряжение на входе (тестером). Избегать работы схемы на токах более 0,6А на протяжении более 10мин. После такого режима делать паузу на 20 мин. 2. По данным измерений вычислить параметры катушек. Результаты измерений и расчетов записать в таблицу 1. 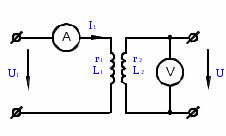 Рис. 4 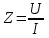 ; ; 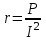 ; ; 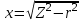 ; ; 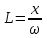 ; ; 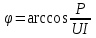 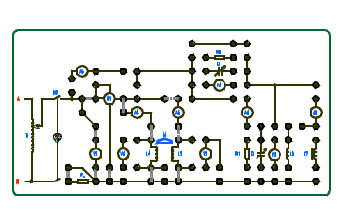 Рис.5. Таблица 1.
3. По схеме рис.6. собрать электрическую цепь для исследования последовательного соединения индуктивно-связанных катушек. Плавно увеличивать напряжение на входе схемы от 0В до получения первого измеряемого отсчета на V4 (24В) при согласном включении. Не меняя напряжения на входе схемы переключить катушки на встречное соединение. Напряжение на V4 измерить тестером. 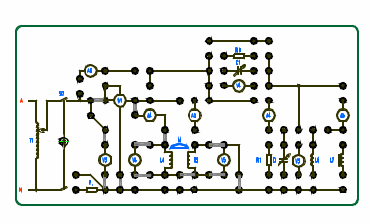 Рис. 6. Измерить ток, мощность и напряжения для согласного и встречного включения катушек при заданном входном напряжении. Определить модуль Z и аргумент полного сопротивления 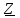 активное rи реактивное х сопротивления, взаимное сопротивление хM и взаимную индуктивность М. активное rи реактивное х сопротивления, взаимное сопротивление хM и взаимную индуктивность М.Результаты измерений и вычислений записать в таблицу 2. Способ включения катушек индуктивности и их одноименные зажимы определяются по значениям тока при Uвх = const. Таблица 2.
4. Используя данные таблиц 1 и 2 построить векторные диаграммы токов и напряжений для согласного и встречного включения катушек. Сравнить результаты расчета xЭ из опыта и по формуле: xЭ = x1 + x2 ±2 xМ. Контрольные вопросы: 1. Что такое согласное и встречное включение индуктивно-связанных катушек? 2. Что понимают под взаимной индуктивностью? 3. От каких факторов зависит взаимная индуктивность двух катушек? 4. Как определяется знак взаимной индуктивности? 5. Как влияет индуктивная связь на эквивалентные реактивные сопротивления катушек при последовательном и встречном включении? 6. Напишите в символической форме выражения для определения падения напряжения на индуктивно-связанных элементах при согласном и встречном включении. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
