Енркер. Методические указания Показатель адиабаты. Лабораторная работа изучение особенностей адиабатного процесса, определение показателя адиабаты воздуха
 Скачать 1.08 Mb. Скачать 1.08 Mb.
|
|
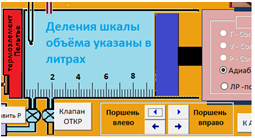
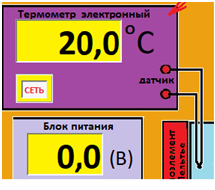
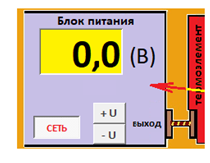
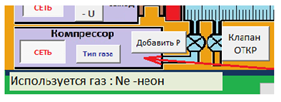
ЛАБОРАТОРНАЯ РАБОТА «ИЗУЧЕНИЕ ОСОБЕННОСТЕЙ АДИАБАТНОГО ПРОЦЕССА, ОПРЕДЕЛЕНИЕ ПОКАЗАТЕЛЯ АДИАБАТЫ ВОЗДУХА» Цель лабораторной работы: изучение закономерностей изменения параметров газа при адиабатном процессе. Задача лабораторной работы: измерение отношения теплоемкостей газа при постоянном давлении и постоянном объеме на основании проведенных измерений. Теоретическая часть Адиабатический процесс (изоэнтропийный процесс, 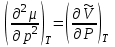 ) - это процесс, происходящий в системе без теплообмена с внешними телами, или это изоэнтропийный процесс, при его протекании энтропия системы не изменяется. ) - это процесс, происходящий в системе без теплообмена с внешними телами, или это изоэнтропийный процесс, при его протекании энтропия системы не изменяется. Запишем первый закон термодинамики для адиабатического процесса: 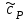 , , 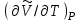 . (1) . (1)Поскольку внутренняя энергия идеального газа 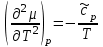 , то используя уравнение Менделеева-Клайперона можно записать , то используя уравнение Менделеева-Клайперона можно записать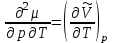 . . По определению теплоемкость при адиабатном процессе 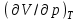 , следовательно , следовательно 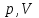 . . Выведем формулу уравнения адиабатического процесса 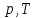 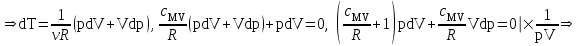 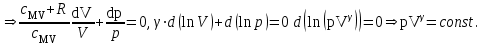 Итак, уравнение адиабаты в параметрах состояния ( 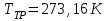 ) принимает вид: ) принимает вид: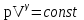 , (2) , (2)а для других параметров идеального газа запишется таким образом: 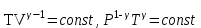 . (3) . (3)При выводе был введен коэффициент Пуассона 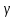 , который равен отношению молярной теплоемкости идеального газа при постоянном давлении к молярной теплоемкости газа при постоянном объеме , который равен отношению молярной теплоемкости идеального газа при постоянном давлении к молярной теплоемкости газа при постоянном объеме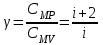 , (4) , (4)причем он выражается через число степеней свободы молекулы идеального газа. где СМР и СMV молярные теплоемкости газа при постоянном давлении и объеме, соответственно. Они связаны между собой уравнение Майера: СМР -СMV =R, (5) где 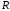 - универсальная газовая постоянная. Показатель Пуассона является важной величиной, поскольку его значение связано со строением молекул газа. В случае идеального газа молярная теплоемкость при постоянном объеме равна - универсальная газовая постоянная. Показатель Пуассона является важной величиной, поскольку его значение связано со строением молекул газа. В случае идеального газа молярная теплоемкость при постоянном объеме равна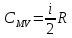 . (6) . (6)где i – число механических степеней свободы молекулы газа. Тогда из соотношения Майера получим 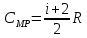 , (7) , (7)а для показателя Пуассона 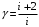 . (8) . (8)Таким образом, показатель Пуассона зависит только от числа степеней свободы молекул газа, которое равно числу независимых движений молекулы газа. Одно-атомная молекула имеет три степени свободы – перемещение центра масс по трем направлениям в пространстве i = 3. Двух-атомная молекула, с жесткой связью атомов, имеет две дополнительных степени свободы, соответствующие вращению вокруг двух взаимно перпендикулярных осей, проходящих через центр масс i = 5. Трех (и более)- атомная молекула, с жесткой связью атомов, имеет еще одну дополнительную степень свободы, так как может вращаться вокруг трех взаимно перпендикулярных осей i = 6. соответственно значения показателя Пуассона для газа из одно-атомных молекул равно 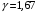 , для газа из двух-атомных молекул равно , для газа из двух-атомных молекул равно 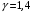 и для газа из трех-атомных молекул оно равно и для газа из трех-атомных молекул оно равно 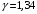 . . Параметр 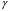 является существенной термодинамической характеристикой газа и используется для сравнения многих теоретических моделей процессов в газах с реальными, например, для теоретического вывода зависимости скорости звука в газе от плотности и давления. является существенной термодинамической характеристикой газа и используется для сравнения многих теоретических моделей процессов в газах с реальными, например, для теоретического вывода зависимости скорости звука в газе от плотности и давления. При очень быстром сжатии газа из некоторого состояния 1 (объем 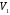 и давление и давление 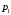 ) с температурой ) с температурой 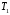 , равной температуре окружающей среды, до некоторого состояния 2 (объем , равной температуре окружающей среды, до некоторого состояния 2 (объем 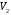 и давление и давление 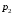 ) процесс сжатия можно считать адиабатическим, так как теплообмен между газом и окружающей средой не успеет произойти. Такой процесс изображен на рис. 1 (верхняя кривая). ) процесс сжатия можно считать адиабатическим, так как теплообмен между газом и окружающей средой не успеет произойти. Такой процесс изображен на рис. 1 (верхняя кривая). При очень медленном сжатии газа, теплообмен с окружающей средой успевает выравнивать температуру газа и окружающей среды в каждый момент процесса и реализуется изотермический процесс, изображенный на рис. 1 (нижняя кривая). Если при этом начальное состояние для адиабатического и изотермического процессов одно и то же 1, а в конечных состояниях 2 и 3 объемы равны 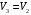 , то, поскольку показатель Пуассона всегда больше единицы, кривая адиабатического процесса сжатия расположена выше кривой изотермического сжатия при сжатии из одного начального состояния (см. рис. 1). Поэтому при равных объемах в конечном состоянии адиабатического процесса, давление выше, чем в конечном состоянии изотермического процесса , то, поскольку показатель Пуассона всегда больше единицы, кривая адиабатического процесса сжатия расположена выше кривой изотермического сжатия при сжатии из одного начального состояния (см. рис. 1). Поэтому при равных объемах в конечном состоянии адиабатического процесса, давление выше, чем в конечном состоянии изотермического процесса 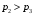 . .В тоже время уравнение состояния газа 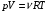 , (9) , (9)выполняется в любом процессе, поэтому температура в точке 2 (рис.1. Кривая 1-2 - адиабата) выше, чем в точке 3 (кривая 1-3 - изотерма), то есть 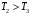 . .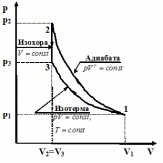 Рис. 1. График процессов, реализуемых в лабораторной работе. Если мы достигли состояния 2 в процессе 1 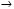 2, а затем предоставляем газу возможность остывать без изменения объема, то реализуется изохорический процесс 2 2, а затем предоставляем газу возможность остывать без изменения объема, то реализуется изохорический процесс 2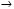 3. В конечном состоянии этого процесса температура окажется равной температуре окружающей среды, то есть температуре начального состояния, как адиабатического, так и изотермического процесса 1 3. В конечном состоянии этого процесса температура окажется равной температуре окружающей среды, то есть температуре начального состояния, как адиабатического, так и изотермического процесса 1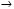 3 3 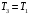 . . В данной работе как раз и реализуются процессы 1 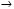 2 2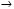 3. Газ, заключенный в цилиндре, быстро сжимается за счет надавливания на поршень (см. рис. 2, верхняя позиция). Состоянию 2 на рис. 2 соответствует средняя позиция. Конечной стадии изохорического процесса (состояние 3) соответствует нижняя позиция на рис. 2. 3. Газ, заключенный в цилиндре, быстро сжимается за счет надавливания на поршень (см. рис. 2, верхняя позиция). Состоянию 2 на рис. 2 соответствует средняя позиция. Конечной стадии изохорического процесса (состояние 3) соответствует нижняя позиция на рис. 2.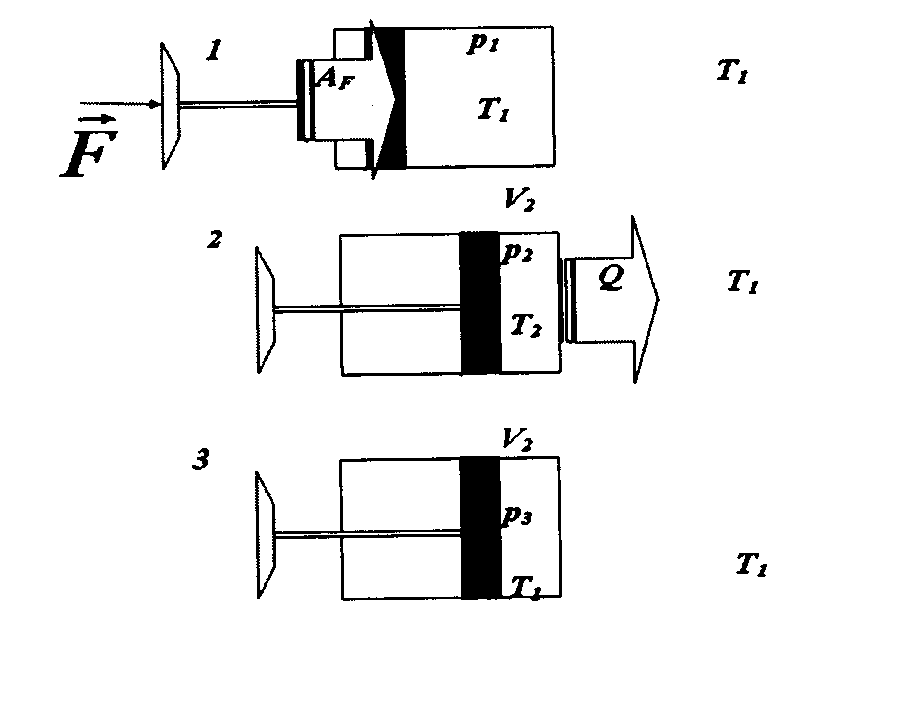 Рис. 2. Схема процессов, реализуемых в лабораторной работе Д  авление газа измеряется датчиком давления, который позволяет регистрировать быстрые изменения этой величины. Вид кривой изменения давления газа в процессе 1 авление газа измеряется датчиком давления, который позволяет регистрировать быстрые изменения этой величины. Вид кривой изменения давления газа в процессе 1 2 2 3 показан на рис. 3. 3 показан на рис. 3.Рис. 3. Вид экспериментальной зависимости P(t) Процесс адиабатического сжатия 1 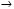 2 описывается уравнением (3) и термодинамические параметры газа в начальном и конечном состоянии процесса связаны соотношением 2 описывается уравнением (3) и термодинамические параметры газа в начальном и конечном состоянии процесса связаны соотношением 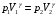 (10) (10)При неизменной массе газа под поршнем можно связать начальные параметры газа (состояние 1) с их значениями в состоянии 3, после того, как нагревшийся в процессе 1-2газ отдаст внешней среде энергию Q и придет к начальной комнатной температуре 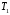 . Действительно параметры газа в состоянии 1 и в состоянии 3 связаныуравнением изотермического процесса (2)или . Действительно параметры газа в состоянии 1 и в состоянии 3 связаныуравнением изотермического процесса (2)или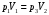 (11) (11)Из уравнений (10) и (11) возведением (11) в степень 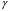 и делением результата на (10) легко получить: и делением результата на (10) легко получить: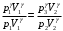 Откуда 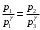 Остается преобразовать его на основании свойства пропорции к виду: 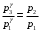 или или 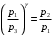 и прологарифмировать: 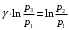 Это выражение можно использовать для получения значения показателя в уравнении адиабаты 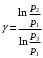 . (12) . (12)если процесс является адиабатическим и квазиравновесным. 2. ЭКСПЕРИМЕНТАЛЬНАЯ УСТАНОВКА Схема реальной установки, смоделированная в данной лабораторной работе представлена на рис. 4. Установка представляет собой прозрачный цилиндр, в котором под поршнем находится исследуемый газ, нагнетаемый в цилиндр компрессором. К цилиндру подсоединены датчики давления и температуры, выводящие показания на измерительные приборы, значение объема газа можно определить по положению поршня на шкале, нанесенной непосредственно на поверхность цилиндра. Внешние условия описываются показаниями барометра и термометра, находящихся в аудитории.  Рис. 4. Вид реальной учебной лабораторной установки для изучения газовых законов. 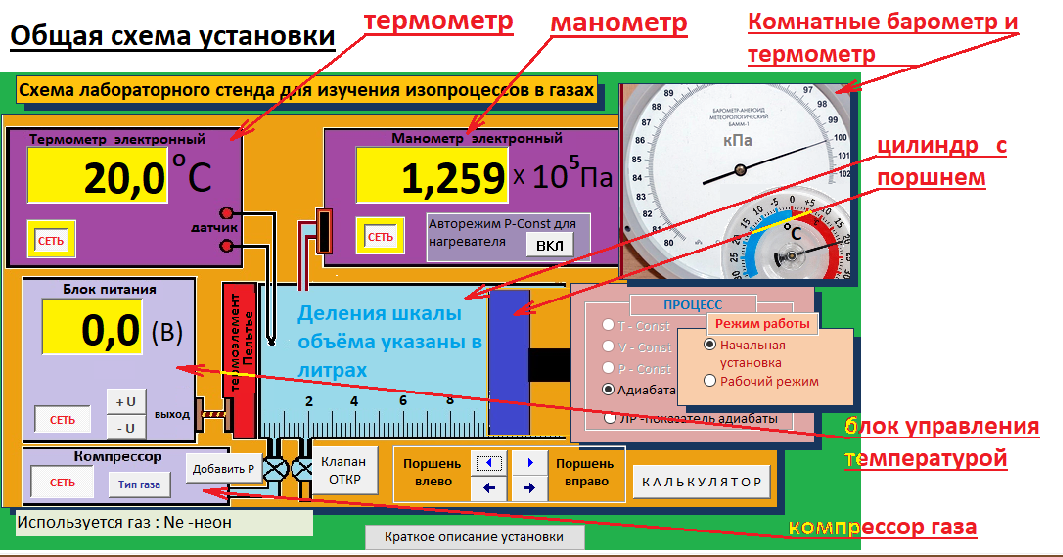 Все перечисленные элементы присутствуют и в данной виртуальной лабораторной работе. На рис. 5 представлена общая схема установки, используемой для изучения газовых законов. Рис. 5. Схема лабораторного стенда для изучения изопроцессов в газах Рассмотрим основные элементы схемы и их роль при проведении эксперимента
Кнопка "Калькулятор" (рис. 12) позволяет вызвать на экран калькулятор, специализированный для данной работы. Он позволяет проводить вычисления в пределах четырех арифметических действий (верхняя часть калькулятора), а также вычислять коэффициент Пуассона (нижняя часть калькулятора). Нужно лишь вводить экспериментальные данные в соответствующие поля и затем нажать кнопку "=". Выбор типа арифметического действия в верхней части калькулятора также осуществляется соответствующими кнопками с указанием типа действия. 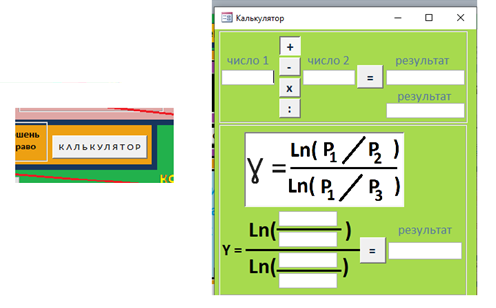 Рис. 12. Калькулятор Служебная часть данной виртуальной лабораторной работы - указатели типа ИЗОПРОЦЕССА и режима работы в рамках этого изопроцесса. Сначала нужно выбрать изопроцесс, а затем определить режим работы. В первую очередь в режиме "Начальная установка" устанавливаются исходные значения объема газа (поршнем ), температуры (с помощью блока питания термоэлемента) и давления (с помощью компрессора). Затем переключаемся в "Рабочий режим" и исследуем поведение газа в рамках данного процесса. 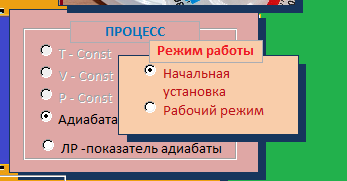 Рис. 13 Панель выбора режима измерений 3. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ Задача 1. Изучение закономерностей адиабатного процесса Скачать на жесткий диск файл «Газ_проектЛР» и открыть его. Включить все блоки установки нажатием кнопки «Сеть». При включении компрессора не выбираем самостоятельно исследуемый газ, тогда по умолчанию в цилиндр «закачивается» воздух. Выбрать процесс «Адиабата», режим «Начальная установка». Сжать газ до минимального объема нажатием кнопки «Поршень влево». Перейти в «Рабочий режим». Увеличивая объем газа нажатием кнопки «Поршень вправо», снять зависимость давления и температуры газа от объема («шаг» изменения объема выбираем произвольным образом). Провести не менее 10 измерений! Результаты измерений записать с таблицу 1. Построить графики Р(V) и Т (V). Сделать выводы о полученных зависимостях (проанализировать, соответствуют или нет адиабатному процессу). Задача 2. Определение показателя адиабаты воздуха Скачать на жесткий диск файл «Газ_проектЛР» и открыть его. Включить все блоки установки нажатием кнопки «Сеть». При включении компрессора не выбираем самостоятельно исследуемый газ, тогда по умолчанию в цилиндр «закачивается» воздух. Выбрать процесс «ЛР – показатель адиабаты», режим «Начальная установка». Устанавливаем поршень в цилиндре на произвольном значении V1. Значение параметров исходного состояния газа Р1 , V1 и Т1 записать в отчет. Установка готова к измерениям. Перейти в «Рабочий режим». Нажать кнопку «Клапан ОТКР». В результате баллон, в котором находится газ, на короткое время с помощью крана соединяют с атмосферой. Таким образом, газу дают достаточно быстро, а, следовательно, адиабатически расшириться до выравнивания давления в баллоне с атмосферным. Дождаться установления исходной температуры Т1 . Значение Р3, установившееся при этом, записать в отчет. За давление Р2 берем комнатное давление 100 кПа. Используя специализированный калькулятор, посчитать показатель адиабаты воздуха. Полученное значение показателя адиабаты сравнить с теоретическим, сделать вывод. ПРИЛОЖЕНИЕ А Форма отчета по лабораторной работе ОТЧЕТ по лабораторной работе №4 ОПРЕДЕЛЕНИЕ ПОКАЗАТЕЛЯ АДИАБАТЫ ВОЗДУХА студент ______________ группа _______________ Дата ________________ Преподаватель _____________ РГППУ 2020 1. Расчетная формула 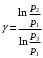 где р1 - давление газа в исходном состоянии 1 при комнатной температуре; р2 - давление газа в состоянии 2 после адиабатического процесса; р3 - давление газа в состоянии 3 после изохорного процесса газа при комнатной температуре. 2. Изучение закономерностей адиабатного процесса Таблица 1
Графики Р(V) и Т (V) 3. Определение показателя адиабаты воздуха Исходные параметры газа: Р1= V1= Т1= Давление газа в конечном состоянии Р3= Расчет показателя адиабаты воздуха: γ= Вывод: |