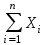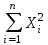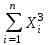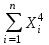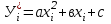Лабораторка комп. Лабораторная работа Математическая обработка результатов эксперимента с использованием метода наименьших квадратов
 Скачать 58.68 Kb. Скачать 58.68 Kb.
|
|
Лабораторная работа «Математическая обработка результатов эксперимента с использованием метода наименьших квадратов» При математической обработке результатов эксперимента часто пользуются графическим изображением функциональных зависимостей между исследуемыми величинами. Но экспериментальные данные могут содержать ошибки, искажающие истинную картину наблюдаемой закономерности. Чтобы математически более или менее точно выразить наблюдаемую закономерность, нужно по возможности устранить случайные отклонения и найти наиболее характерные точки. Метод наименьших квадратов - является наиболее точным методом, с помощью которого достигается сглаживание или выравнивание экспериментальных данных. Задание При выполнении лабораторной работы необходимо решить следующие задачи (каждую задачу необходимо решить на отдельном листе Excel, отредактировав исходные данные, прибавив к каждому значению х номер варианта и к каждому значению у, номер варианта * 0,1): Задача 1. При изучении растворимости азотнокислого натрия NaNO3 (у) в зависимости от температуры (х) раствора получили следующие результаты:
Предполагая, что количество NaNO3 (у) линейно зависит от температуры (х) раствора, выровнять эти экспериментальные данные по прямой у= ах +в. Алгоритм решения Занесите значения Xi и Уi в электронную таблицу Excel (таблица 1). Таблица 1 – Расчетная таблица
Для расчета параметров а и в найдите  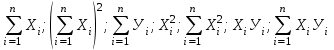 Рассчитайте параметры а и в по формулам: 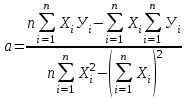 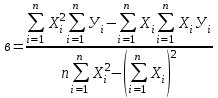 Запишите уравнение у = ах + в, подставив значения коэффициентов а и в. Заполните таблицу 2, найдя 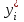 из уравнения из уравнения 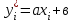 Таблица 2 – Проверка уравнения
По результатам таблицы 2 постройте точечные графики, добавьте линию тренда с уравнением. Сравните полученные результаты. Задача 2. На опыте была получена зависимость процентного содержания воды в смеси эфира с водой (У,%) от температуры кипения (Xi, C).
Выровняйте зависимость у от х по параболе у = ах2 + вх + с, наилучшим образом согласующуюся с экспериментальными данными. Алгоритм решения Составьте вспомогательную таблицу 3. Таблица 3 – Промежуточные расчёты
Рассчитайте параметры а, в и с, используя систему уравнений и поиск оптимального решения в Microsoft Excel. 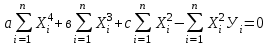 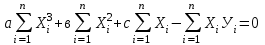  Запишите уравнение сглаживающей параболы. Заполните таблицу 4. Таблица 4 – Проверка уравнения
По результатам таблицы 4 постройте график и сделайте вывод. Задача 3 (состоит из 3 частей) Измерения некоторой величины У в зависимости от значений величины Х привели к следующим результатам:
Постройте график с линией тренда, предполагая, что у = ах + в. По данным следующей таблицы подберите формулу вида у = ах2 + в, пользуясь методом наименьших квадратов:
Предполагая, что у = ах2 + вх + с найдите коэффициенты следующей зависимости и постройте график.
|

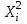


 Уi
Уi