проверка основного закона динамики вращательного движения. Лабораторная работа N2 1 03 проверка основного закона динамики вращательного движения студента группы

• Название: Лабораторная работа N2 1 03 проверка основного закона динамики вращательного движения студента группы
• Анкор: проверка основного закона динамики вращательного движения
• Дата: 24.03.2022
• Размер: 0.55 Mb.
• Имя файла: Laba_103.docx
• Тип: Лабораторная работа; #414388

ТЕХНОЛОГИЧЕСКИЙ ИНСТИТУТ

ЮЖНОГО ФЕДЕРАЛЬНОГО УНИВЕРСИТЕТА

Кафедра физики

Лабораторная работа N2 1 03

ПРОВЕРКА ОСНОВНОГО ЗАКОНА ДИНАМИКИ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ

студента: группы:

	ДОПУСК		ВЫПОЛНЕНИЕ
дата		подпись	дата	подпись

ТАГАНРОГ 2007

2

1. 
   Изучаемое физическое явление:
   

Основной закон динамики вращательного движения. Момент силы. Момент инерции. Момент импульса.

2. 
   Формулировка поставленной задачи:
   

Проверить основной закон динамики вращательного движения

З. Таблица характеристик измерительных приборов:

Название ибо а	Диапазон изме ений	Число делений	Класс точности	Приборная по ешность	Цена деления
линейка
сек ндоме
штангенц ль

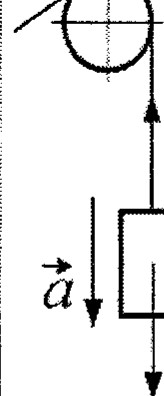
4. Описание лабораторной установки и вывод расчетных формул.

Основной закон динамики вращательного движения в векторной и скалярной формах имеет вид:



где М — момент силы, 1— момент инерции и ё — угловое ускорение.

В проекциях на ось 0Z основной закон динамики вращательного движения запишется



Проверка закона заключается в том, чтобы экспериментально установить прямую пропорциональную зависимость проекции углового ускорения е от момента силы М при заданном моменте инерции I.

Эксперименты проводятся на установке, схематически показанной на рис. 1. Вращающаяся часть установки (маятник Обербека) состоит из четырех спиц 1 , ввинченных во втулку под прямым углом друг к 5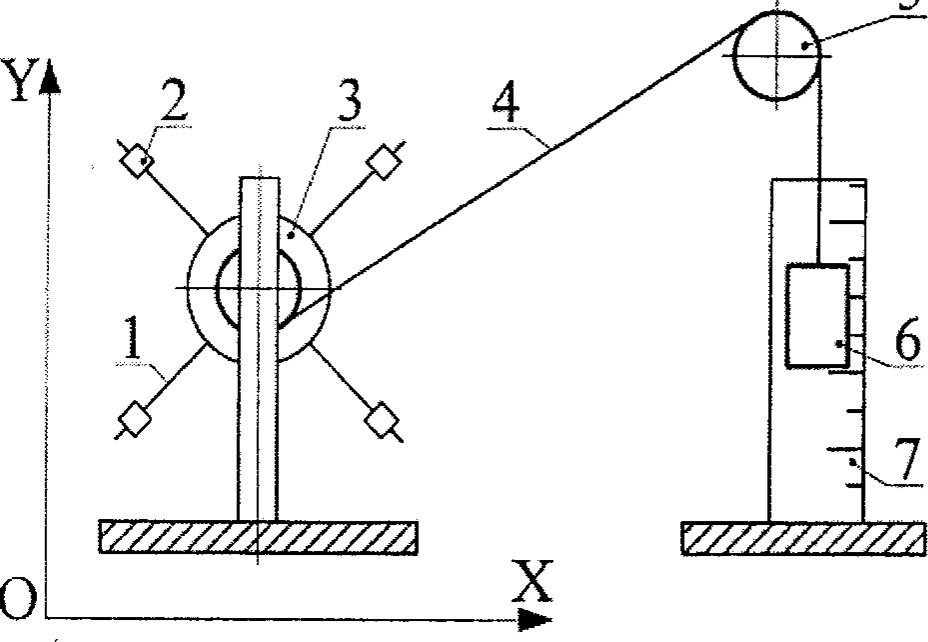

д ругу. На спицы надевается четыре груза 2, которые могут перемещаться по спицам и закрепляться зажимными винта ми на определенном расстоянии от оси. На втулку насажены два легких шкива 3 различных радиусов. Момент силы, вызывающий враще7 ние маятника, создается натяжением нити 4, намотанной на один из шкивов.

Нить перебрасывается через блок 5 и прикрепляется к гире 6. При опускании гиРис. 1 ри нить разматывается и раскручивает маятник. Пройденный гирей путь Н отсчитывается по шкале 7. Момент инерции маятника Обербека можно изменять, перемещая грузы по спицам. Закрепив грузы в каком-либо положении, можем найти связь между моментом инерции маятника и ускорением гири.

Для опускающейся гири, движущейся поступательно, по второму закону Ньютона запишем (рис. 2):

З тб = тп + Tl

ТД х

УА где т— масса груза; б — его ускорение; Tl сила натяжения нити, действующая на гирю.

В проекциях на ось ОУ второй закон Ньютона имеет вид:

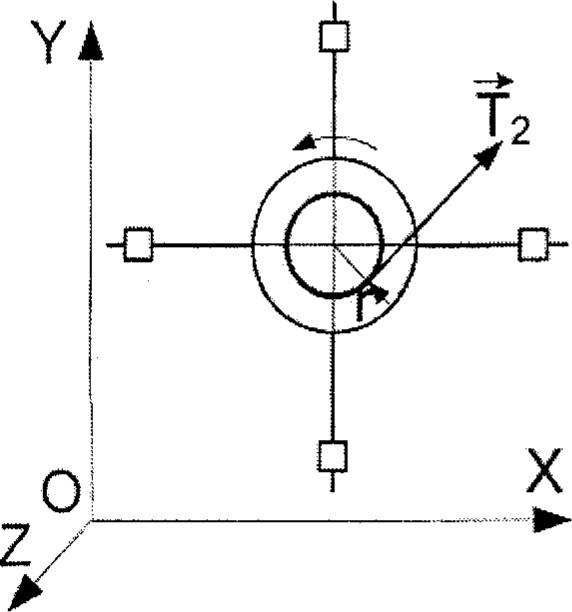
та = ТД — Tl , (1) Для маятника Обербека основной закон динамики вращательного движения в проекциях на ось 0Z запишется (рис. 3)

О (2)

Рис. 2 где I момент инерции маятника относительно оси 0Z; 8 — его угловое ускорение; М— вращающий момент силы Ђ; r радиус шкива. Пренебрегая массами блока и нити, трением в подшипниках и считая нить нерастяжимой и невесомой, получим Т1 = Ђ = Т, тогда уравнения (1) и (2) примут вид та = тд — Т , (3) (4)

Д ля нерастяжимой нити величина ускорения гири а будет равна величине касательного ускорения точек поверхности шкива маятника а=ав. (5) Величину ускорения опускающейся гири можно определить, зная высоту Н и время опускания гири соотношения

(6)

Рис. З

Решая совместно систему уравнений (3) -- (4), получим выражение для момента инерции маятника Обербека

2 gt2

I = mr -1 (7)

и выражение для величины момента силы, действующей на маятник,

(8)

В полученных формулах экспериментально определяются r, t, Н, величина т указана на лабораторном столе. Из уравнения (2) следует, что при постоянном моменте инерции I для различных вращательных моментов должно выполняться условие

(9)

Для проверки справедливости условия (9) целесообразно построить график зависимости г = ЛМ) при I = const по экспериментальным результатам.

5. 
   Результаты измерений и их обработка.
   

   п/п	м	кг					п	а = 0,95
   10
   12

6. 
   Формулы для оценки погрешностей косвенных измерений.
   

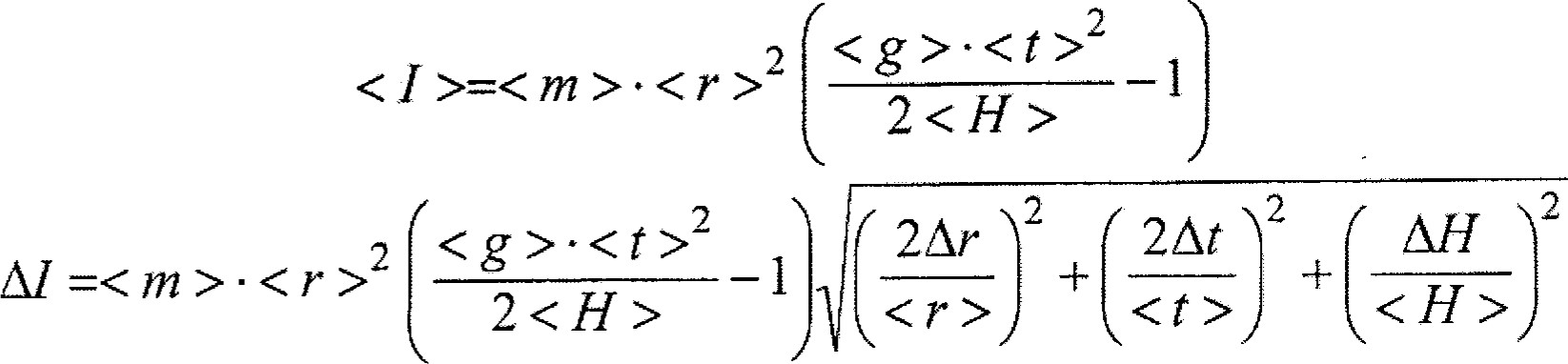
п/п	м			ад•с-	нм	кг•м		кг•м	кг•м
10
11
12

5. 
   Запись окончательного результата.
   

Результаты измерений представить в виде I = (< I > ± М), кг•м

п/п	1 = (< I> ± дг), кг•м2	(< Icp > ± М), КГ•М2
10
12

рад

вывод: