ОПРЕДЕЛЕНИЯ ПОСТОЯННОЙ СТЕФАНА-БОЛЬЦМАНА С ПОМОЩЬЮ ОПТИЧЕСКОГО ПИРОМЕТРА. Физика 3. Лабораторная работа определения постоянной стефанабольцмана с помощью оптического пирометра
 Скачать 119.07 Kb. Скачать 119.07 Kb.
|
|
Лабораторная работа ОПРЕДЕЛЕНИЯ ПОСТОЯННОЙ СТЕФАНА-БОЛЬЦМАНА С ПОМОЩЬЮ ОПТИЧЕСКОГО ПИРОМЕТРА Выполнил: Константин Игоревич Русанов Проверил: Лев Семенович Кудин Цель работы: определить постоянную Стефана-Больцмана посредством изучения излучения нечерного тела - вольфрамовой спирали. Приборы и принадлежности: оптический пирометр с исчезающей нитью, лампа накаливания с вольфрамовой спиралью, трансформатор, амперметр, вольтметр, источник постоянного тока Б5-30. Теоретическое введение Электромагнитное излучение, причиной которого является возбуждение атомов и молекул вещества вследствие их теплового движения, называется тепловым излучением. Наиболее просто законы теплового излучения формулируются для так называемого абсолютно черного тела. Под последним понимают тело, целиком поглощающее всю падающую на него лучистую энергию. По поглощающим свойствам к абсолютно черному телу близки такие вещества, как: сажа, платиновая чернь, черный бархат. Хорошей моделью абсолютно черного тела является полость с малым отверстием. Важной характеристикой теплового излучения является интегральная испускательная способность (интегральная светимость) RT излучающей поверхности. Она представляет собой энергию, излучаемую с единицы площади за единицу времени во всем интервале длин волн RT = Wизл/ (S*t) (1) Здесь Wизл - количество излученной энергии с поверхности S за время t. Стефан и Больцман установили, что интегральная испускательная способность абсолютно черного тела RАЧТ пропорциональна четвертой степени абсолютной температуры, т.е. RАЧТ = T 4 (2) Коэффициент пропорциональности , получивший название постоянной Стефана-Болъцмана, является универсальной постоянной. Для нечерных тел на основании закона Кирхгофа вместо (2) можно записать RT = a T 4 Или RT = a RАЧТ (3) где a - интегральная поглощательная способность тела. Она показывает, какая доля равновесного излучения, падающего на тело, поглощается этим телом a = Wпогл /Wпад (4) Поглощательная способность тела зависит от температуры и различна для разных тел. Для абсолютно черного тела a = 1. Если тело находится в тепловом равновесии с окружающей средой, то количество энергии, излучаемой телом, должно быть равно количеству поглощаемой энергии Wизл = Wпогл. Поскольку Wизл = R*S*t, а Wпогл = a *Wпад, то R*S*t = a*Wпад. С учетом уравнения (3) имеем Wпад = RАЧТ *S*t (5) На основании этого можно сделать вывод: при тепловом равновесии на поверхность любого тела падает столько энергии, сколько излучалось бы этим телом, если бы его поверхность была абсолютно черной. Рассмотрим неравновесное стационарное излучение вольфрамовой спирали, когда ее температура Т отличается от температуры окружающей среды Т0 (Т > Т0) Спираль нагревается электрическим током и потребляет мощность N = U*I, где U и I – соответственно, напряжение и сила тока. Кроме того, спираль поглощает часть падающего на нее излучения, которое зависит от температуры окружающих тел и будет таким же, как при тепловом равновесии при температуре Т0. В соответствии с формулой (5) за 1 сек на спираль падает энергия RАЧТ*S = *T04*S Поскольку спираль является серым телом, поглощается лишь часть этой энергии, равная a0**T04*S. С другой стороны, количество излученной энергии определяется температурой самой спирали и за 1 сек составит величину a**T4*S (см. формулу (3)). По закону сохранения энергии имеем a**T4*S = U*I + a0**T0 4 *S. Откуда = (U* I) /((a*T4 – a0*T04 )*S) (6) Если Т >> Т0, то членом a0 T04 можно пренебречь, и постоянная Стефана-Больцмана определится из формулы = (U *I)/( a*T4*S) (7) Описание экспериментальной установки Схема включения спирали электролампы в электрическую цепь, подсоединенную к вторичной обмотке понижающего трансформатора, приведена на рис. 1. Сила тока через лампу и напряжение на ней регулируются с помощью реостата R и измеряются амперметром и вольтметром. Температура раскаленной спирали измеряется оптическим пирометром с исчезающей питью.  Оптическая схема и общий вид пирометра изображены, соответственно, на рис. 2 и 3, где: 1 - объектив зрительной трубы пирометра, 5 - окуляр, 3 - эталонная лампа, нить которой питается от источника тока через реостат и миллиамперметр (располагается в фокальной плоскости объектива). Резкость изображения достигается с помощью вращения винта 7 и оправы окуляра 5. Между окуляром и лампой пирометра расположена кассета светофильтров 4 для получения монохроматического света. При правильной установке прибора в середине поля зрения окуляра видна спираль исследуемой лампы. Точно в центре поля зрения видна круглая диафрагма окуляра и вершина нити эталонной лампы, находящаяся примерно на середине диафрагмы (рис.4). 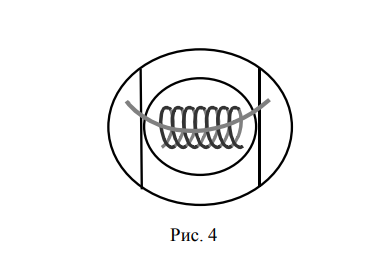 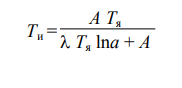 Tи =(1,433*10-2 *1450)/(6,6*10-7*1450*(-0,92)+ 1,433*10-2)=1544,92 =1545  σ=(3,4*3)/(0,4 *15454*0,7*10-4)=6,3*10-8 Относительная погрешность 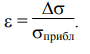 ε=1,03*10-8/6,63*10-8=0,15 Вывод: В ходе лабораторной была определена постоянная Стефана-Больцмана посредством изучения излучения нечерного тела - вольфрамовой спирали. Погрешность составила 6,63*10-8 ± 1,03*10-8[Bт/м2*К4], ε=0,15. Причиной погрешности может быть приборная погрешность , человеческий фактор.
|
