Лабораторная работа по курсу "Общая физика" определение удельного заряда электрона

• Название: Лабораторная работа по курсу "Общая физика" определение удельного заряда электрона
• Дата: 20.04.2023
• Размер: 0.6 Mb.
• Имя файла: 5f9171b.doc
• Тип: Лабораторная работа; #1075782
• страница: 3 из 3

20. Протон и электрон, ускоренные одинаковой разностью потенциалов, влетают в однородное магнитное поле. Во сколько раз радиус кривизны траектории протона будет больше радиуса кривизны траектории электрона?

Частица, пройдя ускоряющую разность потенциалов U, приобретает кинетическую энергию, равную:

( 5.20.1)

где q, m – заряд и масса частицы;

v – скорость, которую приобретает частица.
Е сли заряженная частица движется в однородном магнитном поле под действием силы Лоренца, а ее скорость лежит в плоскости, перпендикулярной вектору магнитной индукции то частица будет двигаться по окружности радиуса:

(5.20.2)



Из уравнения (5.20.1) найдем скорость частицы:

Полученное выражение для скорости частицыv подставим в уравнение (5.20.2):

(5.20.3)

Заряды протона и электрона равны по величине и противоположны по знаку: |q_p| = |q_e| = |e|

С учетом равенства абсолютной величины зарядов и на основании формулы (5.20.3) запишем соотношение радиусов кривизны траекторий частиц:



В справочной литературе приведено соотношение масс протона и электрона − m_p/m_e = 1836,15267.

О кончательно получаем:

21. Протон и электрон влетают в однородное магнитное поле с одинаковой скоростью. Во сколько раз радиус кривизны траектории протона будет больше радиуса кривизны траектории электрона?
Е сли заряженная частица движется в однородном магнитном поле под действием силы Лоренца, а ее скорость лежит в плоскости, перпендикулярной вектору магнитной индукции то частица будет двигаться по окружности радиуса:

(5.21.1)
где q, m – заряд и масса частицы;

Заряды протона и электрона равны по величине и противоположны по знаку: |q_p| = |q_e| = |e|

На основании формулы (5.21.1)запишем соотношение радиусов кривизны траекторий частиц при условии равенства их скоростей:


В справочной литературе приведено соотношение масс протона и электрона − m_p/m_e = 1836,15267.

О кончательно получаем:
22. Показать, что какой бы скоростью v ни обладал электрон, влетающий в однородное магнитное поле с индукцией В, и каким бы ни был угол между векторами v и В, время Т, за которое он опишет виток винтовой линии, будет одним и тем же.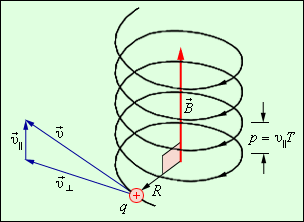



Рисунок 4.18.5.

Движение заряженной частицы по спирали в однородном магнитном поле.

Если скорость частицы имеет составляющую вдоль направления магнитного поля, то такая частица будет двигаться в однородном магнитном поле по спирали. При этом радиус спирали R зависит от модуля перпендикулярной магнитному полю составляющей вектора , а шаг спирали p – от модуля продольной составляющей (рис. 4.18.5). Таким образом, траектория заряженной частицы как бы навивается на линии магнитной индукции.

В направлении перпендикулярном полю частица движется по инерции равномерно, со скоростью
В направлении поля частица движется по инерции равномерно, со скоростью
Угол α в этих выражениях равен углу между скоростью и вектором магнитной индукции  .

В направлении, перпендикулярном вектору магнитной индукции , частица будет двигаться по окружности радиуса:
где m,v,q – масса, скорость и заряд частицы.

 

Период обращения частицы в однородном магнитном поле равен: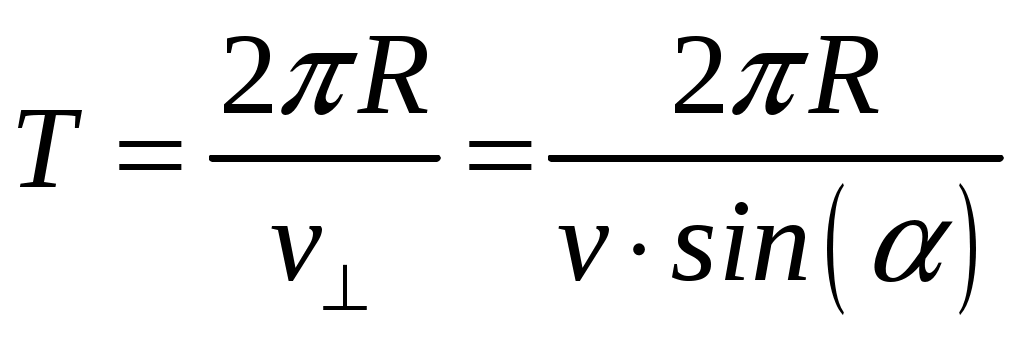




Подставляя сюда вместо R его выражение, имеем: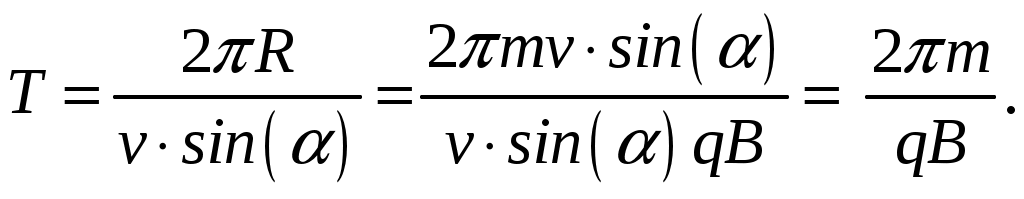



Следовательно, какой бы скоростью v ни обладал электрон, влетающий в однородное магнитное поле с индукцией В, и каким бы ни был угол между векторами v и В, время Т, за которое он опишет виток винтовой линии, будет одним и тем же.
23. Показать, что радиус кривизны траектории заряженной частицы, движущейся в однородном магнитном поле, перпендикулярном её скорости, пропорционален импульсу частицы.

Сила Лоренца является центростремительной силой и при движении частицы в данных условиях справедливо равенство:


где q, m – заряд и масса частицы;

v – скорость электрона;

B – индукция магнитного поля;

r – радиус кривизны траектории.
П од действием магнитного поля траектория движения электрона станет криволинейной. Из приведенного равенства следует, что радиус кривизны траектории зависит от скорости электрона и от величины магнитной индукции поля соленоида:
Импульс частицы равен: p = mv, подставляя в вышестоящее равенство, получим: