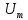Главная страница
Навигация по странице:

  • 1 ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ И МЕТОДИКА ИЗМЕРЕНИЙ

  • 2 ОСНОВНЫЕ РАСЧЕТНЫЕ ФОРМУЛЫ

  • 3 РЕЗУЛЬТАТЫ РАБОТЫ И ИХ АНАЛИЗ

  • R =

    		•

    Изучение затух кол. Лабораторная работа по курсу общей физики Изучение затухающих


    Скачать 63.01 Kb.
    НазваниеЛабораторная работа по курсу общей физики Изучение затухающих
    Дата09.02.2023
    Размер63.01 Kb.
    Формат файлаdocx
    Имя файлаИзучение затух кол.docx
    ТипЛабораторная работа
    #927499

    Министерство науки и высшего образования

    Российской Федерации

    Федеральное государственное бюджетное образовательное

    Учреждение высшего образования

    ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

    СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)

    Кафедра физики

    ОТЧЕТ

    Лабораторная работа по курсу общей физики

    Изучение затухающих электромагнитных колебаний

    Проверил. Выполнил

    Преподаватель Студент гр. 120-1

    ___________ Палешева Е.В. ___________ Бормотов Е.Д.

    ___________ Дашеев Ц.А.

    Томск 2020

    ВВЕДЕНИЕ

    Целью работы является изучение работы колебательного контура, свободных затухающих электромагнитных колебаний и их характеристик

    1 ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ И МЕТОДИКА ИЗМЕРЕНИЙ

    Схема установки представлена на рисунке 2.1.



    Рисунок 2.1 – Схема экспериментальной установки.

    Схема смонтирована в настольном макете, расположенном рядом с монитором. В качестве резистора RP в колебательном контуре II используется переменный резистор, максимальное значение сопротивления которого (400 Ом) устанавливается поворотом ручки переключателя по часовой стрелке в крайнее положение. При повороте ручки против часовой стрелки в крайнее положение значение сопротивления RP = 0. В этом случае активное сопротивление колебательного контура складывается из сопротивления соединительных проводов контура и активного сопротивления катушки индуктивности, 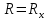. В дальнейшем это сопротивление необходимо рассчитать по результатам измерений. Емкость конденсатора С указана на лабораторном стенде.

    Возбуждение контура производится периодически от импульсов, формируемых компьютером I. Колебания регистрируются осциллографом, представленным на экране монитора. Каждый импульс, подаваемый на колебательный контур, возбуждает один цуг затухающих колебаний. Измерения амплитуды и периода колебаний осуществляются с помощью осциллографа и маркеров, расположенных в углах экрана и перемещаемых с помощью «мыши».

    2 ОСНОВНЫЕ РАСЧЕТНЫЕ ФОРМУЛЫ

    Коэффициент затухания  можно определить по следующей формуле:

    (2.1)

    Где 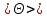- Среднее значение логарифмического декремента затухания;

    - Среднее значение периода колебаний;

    Индуктивность контура рассчитывается по формуле:

    (2.2)

    Где RP = 200 Ом;

    Суммарное активное сопротивление проводников Rx можно найти по формуле: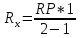

    (2.3)

    Собственную частоту колебательного контура можно рассчитать по формуле: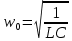

    (2.4)

    Где C – емкость конденсатора равного 0.052 мкФ.

    Частота затухающих колебаний контура рассчитывается по формуле: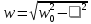

    (2.5)

    Период колебаний контура можно вычислить по формуле: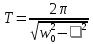

    (2.6)

    Критическое сопротивление можно рассчитать по формуле:

    (2.7)

    Добротность контура можно вычислить по формуле:

    (2.8)

    3 РЕЗУЛЬТАТЫ РАБОТЫ И ИХ АНАЛИЗ

    Результаты измерений представлены в таблице 3.1

    Таблица 3.1 – результаты прямых и косвенных измерений

    Омическое сопротивление контура R
    Номер измеряемой амплитуды n
    Амплитуда

    Логариф-

    мический декремент Θ
    Среднее значение

    < Θ >


    Период колебаний T
    Среднее значение

    < T >

    R =

    1
    6,9
    0,65
    0,58
    0
    0,00096
    0,000966

    2
    3,6
    0,6
    0,65
    0,00098

    3
    2
    0,7
    1,24
    0,00096

    4
    1
    0,36
    1,9
    0,00097

    5
    0,7



    2,3
    0,00096

    R =

    1
    6
    0,7
    0,73
    0
    0,00097
    0,000966

    2
    2,9
    0,73
    0,72
    0,00097

    3
    1,4
    0,8
    1,45
    0,00096

    4
    0,6
    0,69
    2,3
    0,001

    5
    0,3



    3
    0,00093

    Найдем значения коэффициента затухания для R = и R = 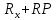по формуле 2.1:

    При R = :



    При R = :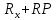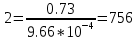



    Найдем индуктивность контура по формуле 2.2:



    Рассчитаем суммарное активное сопротивление проводников Rx по формуле 2.3: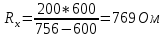



    По формуле 2.4 рассчитаем собственную частоту контура:



    Рассчитаем частоту затухающих колебаний для двух значений сопротивления по формуле 2.5:

    При R = :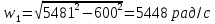



    При R = :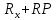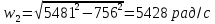



    Рассчитаем периоды колебаний для двух значений сопротивлений по формуле 2.6:

    При R =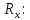



    При R = :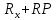



    Рассчитаем критическое сопротивление по формуле 2.7:



    Рассчитаем добротность контура для двух значений сопротивлений по формуле 2.8:

    Для R = :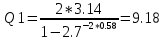



    Для R =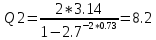



    Заключение

    В результате проделанной работы изучена работа колебательного контура и определены основные характеристики свободных затухающих колебаний δ, ω0, ω, T, Rх, Rкр, Θ, Q .

    При исследовании влияния величины активного сопротивления контура на характер колебаний выяснилось, что величина амплитуды колебаний во времени изменяется (уменьшается) быстрее при увеличении активного сопротивления контура.

    Так как нам удалось построить графики линеаризованной зависимости для двух различных значений активного сопротивления контура и проходящих через экспериментальные точки, то мы убедились в справедливости экспоненциального закона убывания амплитуды со временем.

    написать администратору сайта