Лабораторная работа по общей физике 31. Некоторые законы случайных событий

• Название: Лабораторная работа по общей физике 31. Некоторые законы случайных событий
• Анкор: a[fpsd[pfoew[rqr
• Дата: 18.04.2023
• Размер: 145 Kb.
• Имя файла: lab-stat.doc
• Тип: Лабораторная работа; #1071608

Нижегородский Государственный университет им. Н.И. Лобачевского.

Высшая школа общей и прикладной физики.

Лабораторная работа по общей физике № 31.

Некоторые законы случайных событий.

Целью настоящей лабораторной работы является знакомство с основными законами случайных событий. В описании приводятся элементарные сведения из теории вероятностей и теории ошибок.

Теоретическая часть

В современной науке и технике изучаются и широко используются статистические законы, которым подчиняются различные случайные события. В радиофизике уделяется много внимания таким случайным явлениям, как шум усилителей, нестабильность генераторов, рассеяние волн на случайных неоднородностях среды и другим. Не менее важные примеры можно привести из других разделов физики.

Любое измерение, с какой бы тщательностью оно ни выполнялось, не дает абсолютно точного результата, поэтому, приступая к работе в лаборатории, необходимо иметь некоторые сведения о статистических законах, чтобы оценивать точность измерений.

Систематическое изложение статистических понятий и законов составляет содержание математической дисциплины «теория вероятностей» и специальных разделов физики (статистическая механика, статистическая радиофизика и т.п.)

Цель этой работы – познакомиться на простых примерах с некоторыми понятиями, которыми пользуются для описания случайных явлений, и некоторыми статистическими законами.

Случайное событие. Познакомимся с этим понятием на примере случайных явлений, которые можно наблюдать в опытах с доской Гальтона. Это доска, поставленная вертикально, в которую набито много гвоздей. На гвозди можно бросать через воронку дробинки или сыпать зерна. Упавшие частицы попадают в ряд ячеек, расположенные внизу. Бросим дробинку в воронку доски Гальтона. Она совершит сложный путь по гвоздям и упадет в одну из ячеек. Проделаем много раз такой опыт, соблюдая с максимальной тщательностью неизменность условий опыта, и убедимся, что опыты невозможно абсолютно точно воспроизвести. Дробинки летят по-разному. Попадание одной дробинки в какую-то ячейку назовем событием. Чтобы выразить то обстоятельство, что при самом тщательном соблюдении постоянства контролируемых внешних условий дробинки летят по разным путям, которые нельзя до опыта предсказать, говорят: падение дробинки – случайное событие.

Случайная величина. Случайное событие можно описывать количественно с помощью случайных величин. Например, номер ячейки, в которую упала частица, путь, пройденный ею, и время падения – это случайные величины, описывающие одно и то же событие.

В рассмотренном примере номер ячейки может принимать только счетное множество значений. Такие случайные величины называют дискретными. Величины, которые принимают непрерывный ряд значений (например, время падения), называют непрерывными случайными величинами.

Относительная частота и вероятность события. Произведем бросание частицы на доску Гальтона N раз. (Можно бросать одну частицу N раз или N одинаковых частиц один раз.) Каждое такое бросание называют испытанием. Обозначим через N_k число испытаний, при которых частица попадает в ячейку с номером k. Отношение N_k/N называется относительной частотой события, заключающегося в попадании частицы в ячейку k. Если произвести несколько серий испытаний с N опытами в каждой серии, то обнаружится, что относительная частота – случайная величина, но чем больше N, тем меньше она меняется от серии к серии. Иначе говоря, N_k/N слабо флюктуирует при большом N. Это свойство будем называть устойчивостью относительной частоты события. Устойчивость относительных частот при большом числе испытаний– частный случай проявления основного статистического закона, который называют законом больших чисел.

Опыт показывает, что относительная частота не зависит от N регулярным образом: с изменением N это отношение, изменяясь случайно, может становиться больше или меньше, чем некоторое постоянное число (чем больше N, тем менее вероятны большие отклонения N_k/N от этого числа). Это число, характеризующее случайное явление, – не случайная величина. Его называют вероятностью события. За приближенное значение вероятности принимают относительную частоту события при достаточно большом числе испытаний. О достаточности числа испытаний можно судить только учитывая требующуюся точность определения вероятности.

Закон распределения. Отложим на графике по оси абсцисс номер ячейки k, а по оси ординат– вероятность попадания частицы в нее P_k. Такой график или таблица значений P_k называется законом распределения случайной величины. В данном примере случайная величина n– номер ячейки, в которую попадает частица. P_k является вероятностью события, состоящего в том, что частица попадает в ячейку k, в то же время можно сказать, что P_k есть вероятность того, что случайная величина n принимает значение k. При большом числе частиц P_k пропорционально в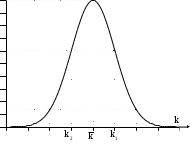




P_k




Рис. 1.
ысоте столбика частиц в ячейке k. В этом случае график имеет вид, изображенный на рис. 1.

К
олоколообразная кривая, которую можно провести через точки на графике зависимости P_k от k будет иметь такую же форму, как и холмик, образованный частицами в ячейках. Эту кривую называют кривой вероятностей.

Обозначим номер средней ячейки доски Гальтона, над которой находится воронка. Средняя ячейка будет наиболее вероятной, т.е. – максимальна. Оказывается, при достаточно большом числе ячеек, для произвольного k вероятность P_k приближенно выражается формулой

, (1)

где .

Величина  в этой формуле характеризует и высоту, и ширину холмика, который образуют частицы, или ширину максимума кривой вероятностей. Чтобы найти связь  с шириной, положим в формуле (1) и . Тогда получим

.

Это значит, что k₁ – k₂ = 2 равняется ширине максимума кривой вероятностей, измеренной на уровне ниже в раз. Есть много случайных величин, для которых закон распределения описывается формулой (1). Такой закон называется нормальным или Гауссовым. Величина  называется стандартом, а ее квадрат – дисперсией. Дисперсия и стандарт характеризуют величину случайных отклонений от среднего значения. Чем меньше , тем реже происходят, т.е. менее вероятны, большие отклонения случайной величины от среднего значения.

Интегральная и дифференциальная функции распределения

непрерывной случайной величины.

Для описания непрерывной случайной величины пользуются двумя функциями: интегральной функцией распределения и дифференциальной функцией распределения, или плотностью вероятности. Поясним эти понятия на примере результатов измерения некоторой величины, например, длины отрезка. Будем обозначать эту величину a.

Так как результат измерения зависит от огромного числа мелких помех, то при одинаковых макроскопических условиях опыта (те же приборы и метод) измерение – это случайное событие, а результат измерения величины a – это непрерывная случайная величина X, которая в зависимости от сочетания многих причин может принимать непрерывный ряд значений.

Пусть измерение величины a выполнили N раз, причем N’ раз получились значения X
. (2)

Функция F(x) называется интегральной функцией распределения случайной величины X. F(x) – безразмерная функция. При изменении x от - до + F(x) монотонно возрастает от 0 до 1. Характер возрастания различен для разных случайных величин.

Плотностью вероятности или дифференциальной функцией распределения называется производная от интегральной функции распределения F(x) по переменной x:

. (3)

Так как F(x) = P(X < x + x) – P(X < x)= P(x < X
Очевидно, интегральная вероятность F(x) может быть выражена интегралом от плотности вероятности

. (4)

Для многих случайных величин, в том числе для случайных результатов измерения, справедлив нормальный закон распределения, или закон Гаусса. В этом случае дифференциальная функция распределения имеет вид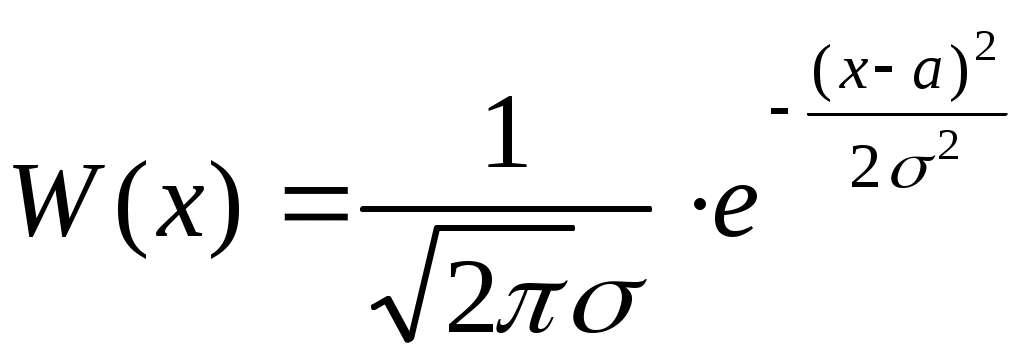

, (5)

г
W(x)
де a и  – постоянные величины.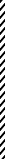







Рис. 2.

W_max



2 




a

x

x





Кривая, изображающая функцию W(x), показана на рис.2. Это колоколообразная кривая с крыльями, прижимающимися к оси абсцисс. При x = a функция W(x) имеет максимум и равна . Значение a называется наиболее вероятным. При x = a   плотность вероятности равна .

Отмеченная на рис. 2 площадка S с основанием x изображает вероятность P попадания случайной величины X в интервал значений x. Так как S = W(x) x, где W(x) – плотность вероятности на интервале x, то случайная величина чаще принимает значения, лежащие в интервалах с большими W(x). Полная площадь под кривой W(x) – это вероятность появления какого-нибудь значения x. Она равна единице.

Интегральная функция распределения, соответствующая плотности вероятности (5), имеет вид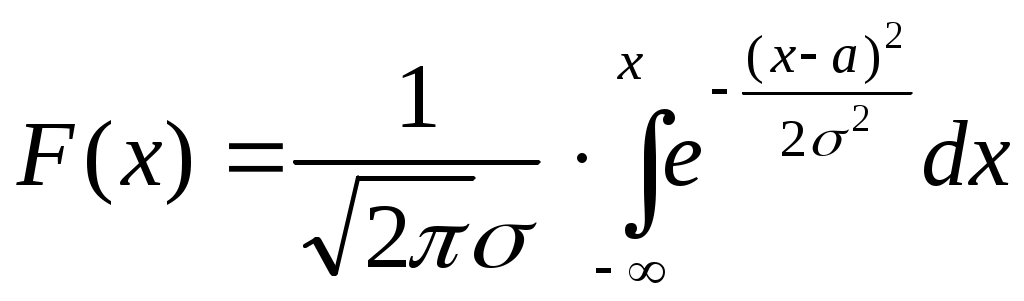

. (6)

И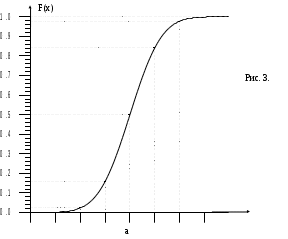
нтеграл (6) не выражается через элементарные функции. Для него составлены таблицы, по которым и построен график функции F(x), изображенный на рис. 3.

И
x

нтегральная функция F(x) = P(X
Среднее значение и дисперсия случайной величины.

Если число испытаний равно N, и из них N_k испытаний дают значения X, лежащие в малом интервале от x_k до x_k + x_k, то сумма значений X, полученных в N_k опытах, будет приближенно равна x_k^.N_k, а сумма значений, полученных при всех N опытах  x_k^.N_k. Разделив эту сумму на N, получим приближенно среднее значение величины X, которое мы будем обозначать (надстрочной чертой над случайной величиной далее будем отмечать операцию усреднения по совокупности N случайных значений этой величины). . При достаточно больших N и N_k относительную частоту можно заменить вероятностью P попадания значения X в интервал x_k, x_k + x_k. Тогда среднее значение . При достаточно малых x_k суммирование можно заменить интегрированием (7)

Интеграл в равенстве (7) величина не случайная. Она называется математическим ожиданием случайной величины X и обозначается M(X). Вероятность отклонения от M(X) при увеличении числа испытаний N стремится к нулю. В этом смысле и надо понимать приближенное равенство .

Для нормального распределения (5) M(X) совпадает с наиболее вероятным значением a, т.е. .

Математическое ожидание является одним из основных параметров, характеризующих распределение вероятности.

Другим важным параметром является дисперсия, она характеризует отклонение случайной величины от среднего значения. Рассмотрим квадрат отклонения случайной величины от среднего значения (x – )². Из расчета, аналогичного тому, который привел к выражению (7), получается . (8)

Правая часть последнего равенства не случайная величина, обозначим ее D. Среднее значение квадрата отклонения случайной величины от своего среднего приблизительно равна D. Приблизительность равенства имеет тот смысл, что при большом числе испытаний редки будут заметные отклонения от D. Величина D называется дисперсией случайной величины. Величина называется стандартом.

Для нормального закона (5) интеграл (8) равен ², т.е. D = ². Таким образом, величина  – это стандарт случайной величины, подчиняющийся нормальному закону, или среднеквадратичное ее отклонение от среднего значения.

Задание 1.

Проследите несколько раз за движением отдельной частицы по доске Гальтона. Зарисуйте приблизительно траектории частиц.

Задание 2.

Выполните три серии испытаний с разными числами N, равными N = 10, N = N₀/2 (половина стакана), N = N₀. Для каждой серии произведите не менее трех опытов. Результаты опытов зафиксируйте следующим образом. При N = 10 запишите в Таблицу 1 номера ячеек, в которые попали частицы, и количество частиц в ячейке:

Таблица 1.

Номер ячейки
1
2
3

Таблица 2.

	5	20	28	35	40
1
2
3

h =
Таблица 3.

	2	4	6	8
1
2
3

h =

При N = N₀/2 в Таблицу 2 занесите высоты столбиков h_k в пяти ячейках (центральной и удаленных от нее на разные расстояния), а также суммарную высоту h столбиков во всех ячейках (не в пяти выбранных, а именно во всех ячейках).

При N = N₀ в Таблицу 3 занесите высоты столбиков h_k во всех четных (или нечетных) ячейках, а также суммарную высоту h столбиков во всех ячейках подряд.

Обработка результатов.

1. 
   Флюктуации относительной частоты.
   

Сравните флюктуации относительной частоты в одной из средних ячеек при разных N. Сравните флюктуации относительной частоты при одном N в одной из средних ячеек и в одной из крайних ячеек. Сравните средние значения относительной частоты при разных N для одинаковых ячеек. Согласуются ли опыты с законом больших чисел?

2. 
   Закон распределения частиц по ячейкам доски Гальтона.
   

Постройте график зависимости вероятности P_k от номера ячейки k. За приближенное значение вероятности примите среднее значение относительной частоты , полученное в опытах с полным стаканом. Значение найдите по экспериментальным данным, зафиксированным в Таблице 3. При построении графика берите больше значений k в области, где h_k быстро меняется при переходе к соседним ячейкам.

Для построения функции P_kт примите за то значение k, при котором получился максимум экспериментальной кривой. Значение стандарта , которое необходимо для построения теоретической кривой P_kт можно вычислить двумя способами: 1) полагая совпадающими максимальные значения функций P_k и P_kт ; 2) принимая, что стандарт  равен полуширине экспериментальной кривой на уровне . Оба способа дадут одинаковые значения , если выполняется закон Гаусса.

Задание 3.

Интегральный и дифференциальный законы распределения для непрерывной случайной величины. Приводятся 2 варианта задания, которые выполняются для разных случайных величин с разной аппаратурой.

А) При изготовлении резисторов с заданным значением сопротивления из-за многих мелких отклонений от нормального технологического процесса получается разброс значений сопротивления R, который можно описать с помощью закона распределения.

Чтобы получить экспериментально этот закон, измерьте при помощи мостика Уитстона сопротивления 100 образцов резисторов с одинаковой маркировкой. Полученные при измерении значения случайной величины R отметьте на числовой оси. Если значения повторяются, отметьте их штрихами над осью. Используя эти измерения, постройте интегральную функцию распределения F(r) для случайного результата измерения R, пользуясь приближенным равенством , где N – общее число измерений. N’ – число значений R, которые меньше r.

Постройте график дифференциальной функции распределения путем графического дифференцирования функции F(r). На том же рисунке постройте график плотности вероятности для нормального распределения 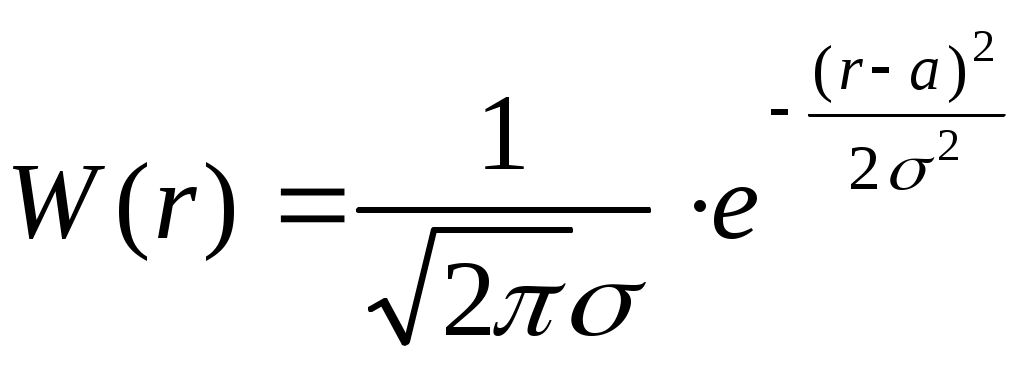. За a примите наиболее вероятное значение величины R, полученное при эксперименте, а за  – полуширину экспериментальной кривой на уровне ( ). Сравните стандарт  с погрешностью, которую дает мостик, использованный для измерений.

Сравните a со значением сопротивления R₀, указанным на резисторах. Сравните систематическую и случайную погрешности изготовления резисторов (a – R₀)/a и /a с погрешностью, указанной на образцах.

Б) Измерьте при помощи мостика УМ-2 емкость 100 образцов конденсаторов с одинаковой маркировкой. Разброс полученных значений емкости C тоже связан со случайными отклонениями от нормального технологического процесса. Результаты обработайте так же, как указано в задании А).