ЛАБОРАТОРНАЯ РАБОТА 2. МОДЕЛЬ НЕЙРОНА. ГРАФИЧЕСКАЯ ВИЗУАЛИЗАЦИЯ. Лабораторная
 Скачать 178.58 Kb. Скачать 178.58 Kb.
|
Лабораторная работа 2. Модель нейрона. Графическая визуализация вычислений в системе MATLAB Цель лабораторных занятийИзучение структурных схем модели нейрона и средств системы MATLAB, используемых для построения графиков функций активации нейрона. Краткие сведения из теорииПростой нейронЭлементарной ячейкой нейронной сети является нейрон. Структура нейрона с единственным скалярным входом показана на рис. 1,а. Вход Нейрон без смещения Вход Нейрон со смещением 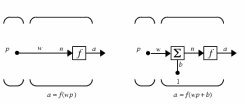 а б а бРис. 1 Скалярный входной сигнал p умножается на скалярный весовой коэффициент w, и результирующий взвешенный вход w*pявляется аргументом функцииактивациинейронаf, которая порождает скалярный выход а. Нейрон, показанный на рис. 1,б, дополнен скалярным смещением b. Смещение суммируется с взвешенным входом w*p и приводит к сдвигу аргумента функции f на величину b. Действие смещения можно свести к схеме взвешивания, если представить, что нейрон имеет второй входной сигнал со значением, равным 1 (b*1). Вход n функции активации нейрона по-прежнему остается скалярным и равным сумме взвешенного входа и смещения b. Эта сумма (w*p + b*1) является аргументом функции активации f, а выходом функции активации является сигнал а. Константы wи b являются скалярными параметрами нейрона. Основной принцип работы нейронной сети состоит в настройке параметров нейрона таким образом, чтобы поведение сети соответствовало некоторому желаемому поведению. Регулируя веса и параметры смещения, можно обучить сеть выполнять конкретную работу; возможно также, что сеть сама будет корректировать свои параметры, чтобы достичь требуемого результата. Уравнение нейрона со смещением имеет вид 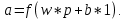 (1) (1)Как уже отмечалось, смещение b – настраиваемый скалярный параметр нейрона, который не является входом. В этом случае b– вес, а константа 1, которая управляет смещением, рассматривается как вход и может быть учтена в виде линейной комбинации векторов входа 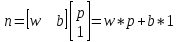 . .Нейрон с векторным входомНейрон с одним вектором входа p с R элементами p1, p2,…, pR показан на рис. 2. Здесь каждый элемент входа умножается на веса w11, w12,…, w1R соответственно, и взвешенные значения передаются на сумматор. Их сумма равна скалярному произведению вектора- строки W на вектор-столбец входа p. Нейрон имеет смещение b, которое суммируется со взвешенной суммой входов. Результирующая сумма 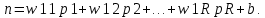 (3) (3)Вход Нейрон с векторным входом 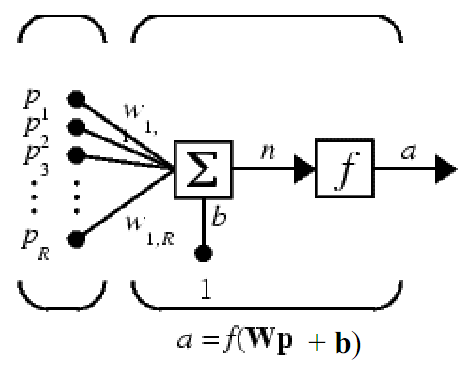 Рис. 2. служит аргументом функции активации f. В нотации языка MATLAB это выражение записывается так: n = W*p + b. Структура нейрона, показанная выше, является развернутой. При рассмотрении сетей, состоящих из большого числа нейронов, обычно используется укрупненная структурная схема нейрона (рис. 3). Вход Нейрон с векторным входом 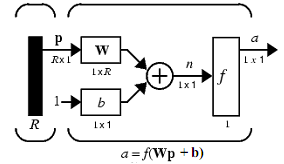 Рис. 3. Вход нейрона изображается в виде темной вертикальной черты, под которой указывается количество элементов входа R. Размер век- тора входа p указывается ниже символа p и равен Rx1. Вектор входа умножается на вектор-строку W длины R. Как и прежде, константа 1 рассматривается как вход, который умножается на скалярное смещение b. Входом nфункции активации нейрона служит сумма смещения b и произведение W*p. Эта сумма преобразуется функцией активации f, на выходе которой получаем выход нейрона а, который в данном случае является скалярной величиной. Структурная схема, приведенная на рис. 3, называется слоем сети. Слой характеризуется матрицейвесовW, смещением b, опе- рациями умножения W*p, суммирования и функцией активации f. Вектор входов p обычно не включается в характеристики слоя. Каждый раз, когда используется сокращенное обозначение сети, размерность матриц указывается под именами векторно-матричных переменных (см. рис. 3). Эта система обозначений поясняет строение сети и связанную с ней матричную математику. Функции активацииФункции активации (передаточные функции) нейрона могут иметь самый различный вид. Функция активации f, как правило, при- надлежит к классу сигмоидальных функций, которые имеют две горизонтальные асимптоты и одну точку перегиба, с аргументом функции n (входом) и значением функции (выходом) a. Рассмотрим три наиболее распространенные формы функции активации. Единичнаяфункцияактивациисжесткимограничениемhardlim Эта функция описывается соотношением a= hardlim(n) = l(n) и показана на рис. 4. 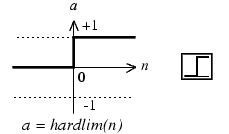 Рис. 4 Она равна 0, если n < 0, и равна 1, если n ≥ 0. Чтобы построить график этой функции в диапазоне значений входа от –5 до +5, необходимо ввести следующие операторы языка MATLAB в командном окне: n = -5:0.1:5; plot(n,hardlim(n),'b+:'); Линейнаяфункцияактивацииpurelin Эта функция описывается соотношением a= purelin(n) = n и показана на рис. 5. 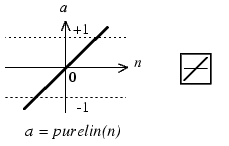 Рис. 5 Чтобы построить график этой функции в диапазоне значений входа от –5 до +5, необходимо ввести следующие операторы языка MATLAB в командном окне: n=-5:0.1:5; plot(n,purelin(n),'b+:'); Логистическаяфункцияактивации logsig Эта функция описывается соотношением a = logsig(n) =1/(1+ +exp(-n)) и показана на рис. 6. 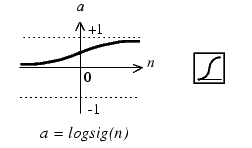 Рис. 6 Данная функция принадлежит к классу сигмоидальных функций, и ее аргумент может принимать любое значение в диапазоне от –∞ до +∞, а выход изменяется в диапазоне от 0 до 1. Благодаря свойству дифференцируемости (нет точек разрыва) эта функция часто используется в сетях с обучением на основе метода обратного распространения ошибки. Чтобы построить график этой функции в диапазоне значений вхо- да от –5 до +5, необходимо ввести следующие операторы языка MATLAB в командном окне: n=-5:0.1:5; plot(n,logsig(n),'b+:'); На укрупненной структурной схеме для обозначения типа функции активации применяются специальные графические символы; некоторые из них приведены на рис. 7, где а– ступенчатая, б – линейная, в – логистическая. 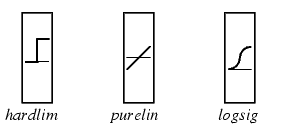 а б в Рис. 7 Построение графиков функций одной переменной в системе MATLABДля построения графика функции одной переменной в системе MATLAB используется оператор plot. При этом графики строятся в отдельных масштабируемых и перемещаемых окнах. Например, для построения графика функции sin xдостаточно вначале задать диапа- зон и шаг изменения аргумента, а затем использовать оператор plot (рис. 8): x=-5:0.1:5; plot(x,sin(x))  Рис. 8 Оператор plot является мощным инструментом для построения графиков функций одной переменной. Он позволяет строить графики сразу нескольких функций и имеет различные формы, синтаксис ко- торых можно узнать, воспользовавшись командой help plot. Порядок выполнения работыПостроить графики функций активации в заданных диапазонах значений в соответствии с вариантом (таблица), используя функцию plot. Используя функцию plot, построить графики всех заданных функций, согласно варианту, в одном графическом окне. Составить отчет, который должен содержать: Содержание отчетаТема лабораторной работы; графики функций; выводы.
|
