Отчет 1. Лекции 1 дифференциальные уравнения и преобразования по курсу основы теории управления
 Скачать 17.62 Kb. Скачать 17.62 Kb.
|
|
ГУАП КАФЕДРА № 14 ОТЧЕТ ЗАЩИЩЕН С ОЦЕНКОЙ ПРЕПОДАВАТЕЛЬ
РАБОТУ ВЫПОЛНИЛ
Санкт-Петербург 2020 РОЛЬ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В НАУКЕ И ТЕХНИКЕ Определение дифференциальных уравненийДифференциальное уравнение – уравнение, в которое входят производные функции и могут входить сама функция, независимая переменная и параметры Дифференциальные уравнения описывают связь между неизвестной функцией и ее производными. Такие связи есть в: механике, физике, химии, биологии, экономике и др, ПрименениеДифференциальные уравнения широко используются в моделях экономической динамики, в которых исследуют не только зависимость переменных от времени, а и от их взаимосвязи во времени. Также применяются для математического описания природных явлений: в биологии – описание популяции; в физике – многие законы описаны с помощью дифференциальных уравнений В биологииМодель Лотки-Вольтерры – модель, описывающее биологические сообщества, популяцию, состоящую из двух взаимодействующих видов. Первый – хищник, при отсутствии второго вымирает по закону 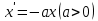 , второй – жертвы, при отсутствии хищников неограниченно размножается в соответствии с законом Мальтуса. Взаимодействие двух этих видов моделируется так. Жертвы вымирают со скоростью, равной числу встреч хищников и жертв, которое в данной модели предполагается пропорциональным численности обеих популяций, т. е. равной , второй – жертвы, при отсутствии хищников неограниченно размножается в соответствии с законом Мальтуса. Взаимодействие двух этих видов моделируется так. Жертвы вымирают со скоростью, равной числу встреч хищников и жертв, которое в данной модели предполагается пропорциональным численности обеих популяций, т. е. равной 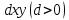 . Поэтому . Поэтому 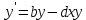 . Хищники же размножаются со скоростью, пропорциональной числу съеденных жертв: . Хищники же размножаются со скоростью, пропорциональной числу съеденных жертв: 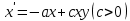 . Система уравнений . Система уравнений 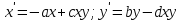 – система Лотки-Вольтерры – система Лотки-ВольтеррыВ физикеВторой закон Ньютона в форме дифференциального уравнения 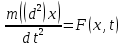 , где m – масса тела, x – его координата, F(x,t) – сила, действующее на тело с координатой x в момент времени t. Его решением является траектория движения тела под действием указанной силы , где m – масса тела, x – его координата, F(x,t) – сила, действующее на тело с координатой x в момент времени t. Его решением является траектория движения тела под действием указанной силы |
