Упражнения на графы. Лекции по ДИСМАТ _ Часть 1-теори множеств. Лекции Дискретная математика

• Название: Лекции Дискретная математика
• Анкор: Упражнения на графы
• Дата: 15.06.2021
• Размер: 1.02 Mb.
• Имя файла: Лекции по ДИСМАТ _ Часть 1-теори множеств.doc
• Тип: Лекции; #217395
• страница: 3 из 4

Пример: А Х = В.

1. 
   шаг ((A X) ) (( ) B) = ,
   

или (A ) (X ) (( ) B) = ,

2. 
   шаг (A ) ( X ) (( B) ) = =>
   
3. 
   ш аг 1) A =
   

2) X =

3) ( B) =

4. 
   шаг В полученном уравнении, в соответствии с описанным его видом (М Х) (N ) R= , имеем R = A , M = , N = B.
   

Исходя теперь из выше указанного условий (R = , N ) существования решения Х, находим, что постоянные множества данного уравнения (А и В) должны быть такими, чтобы выполнялись ограничения: А В и В В.

Второе ограничение выполняется при А и В, поэтому для существования решения данного уравнения должно быть А В. При выполнении данного требования искомым решением будет

Х, такое, что В Х В.

Решение можно записать и в более привычном виде как

Х = (В ) D, где D – любое подмножество множества В.

При решении уравнений следует помнить, что круги и диаграммы Эйлера могут быть использованы для наглядного изображения различных множеств и операций над ними, а также для проверки различных равенств и тождеств. Однако для решений уравнений применять их практически не возможно, что связано с принципиальными трудностями, так как они не содержат полной информации о решениях уравнений и его свойствах.

Графические методы алгебры множеств основаны не только на кругах Эйлера, но и на так называемых диаграммах Венна, которые могут быть использованы и для наглядного представления (изображения) решения уравнений.
9. Символ и диаграмма Венна

Одной из часто встречающихся операций над множеством является разбиение множество на систему подмножеств. Рассмотрим некоторое множество М и систему множеств ={Х₁, Х₂, Х₃,...., Х_n}. Эта система ( ) называется разбиением множества М, на полную систему множеств, если она удовлетворяет следующим условиям:

1. 
   Х_i является подмножеством М, т.е. если Х_i Х_i M (i=1,2,....,n),
   
2. 
   Х_i Х_j= Ø -  Х_i и Х_j , если i j.
   
3. 
   Х_i= М, т.е. - объединение всех Х_i дает множество М.
   

Пусть дано n множеств. Они изображаются в плоскости ­­­­n областями, ограниченными замкнутыми гладкими линиями. (При построении символов и диаграммы Вен­­на -в отличие от диаграммы Эйлера– каждое множество изображается областью, ограниченной произвольной замкнутой линии (квадрат, прямоугольник, круг, овал и др.), причем каждое множество должно иметь одну и только одну общую часть с каждым предыдущим множеством).

При изображении указанным способом “n” множеств, соответствующие их контуры разбивают весь универсум на 2ⁿ непересекающихся частей. Полученное таким образом изображение заданной совокупности множеств универсума называется символом Венна. Эти замкнутые области, как и круги Эйлера, соответствует множествам А₁, А₂, ..., А_n, а каждая из упомянутых (2ⁿ) частей, может быть представлена как пересечение n множеств Ã_i, где -в зависимости от этих частей- Ã_i= = А_i или Ã_i = _i ( i=1, 2,…, n).

Пример: При n = 3, имеем A₁, A₂, A₃ и, соответственно, весь универсум разбивается на 2ⁿ= 8 не пересекающихся частей (подмножеств Х_i) :

I 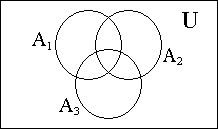- A₁ A₂ A₃ ,

I I - A_{1 2 3} ,

I II - A₁ A_{2 3} , II III IV

IV - ₁ A_{2 3} , _V ^I _VI

V - A_{1 2} A₃ , _VII

VI - ₁ A₂ A₃ , ^VIII

VII - _{1 2} A₃ ,

VIII - _{1 2 3} . Символ Венна при n=3.

Система теоретико –множественные соотношений отображается на символ Венна выделением (штриховкой) тех подмножеств/ячеек, которые соответствует пустому подмножеству. В результате получают диаграмму Вена. При этом объединение всех заштрихованных участков соответствует пустому множеству (Ø), а объединение всех незаштрихованных участков дает универсум (U).

Примеры:

1. 
   Для отображения уравнения с правой частью (равной) Ø следует заштриховать области соответствующие его левой части: А= =>
   

согласно 12⁰ , =U . (В данном примере в универсуме «штрихуется» =А).