Упражнения на графы. Лекции по ДИСМАТ _ Часть 1-теори множеств. Лекции Дискретная математика

• Название: Лекции Дискретная математика
• Анкор: Упражнения на графы
• Дата: 15.06.2021
• Размер: 1.02 Mb.
• Имя файла: Лекции по ДИСМАТ _ Часть 1-теори множеств.doc
• Тип: Лекции; #217395
• страница: 1 из 4

Министерство образования и культуры Кыргызской Республики

Кыргызский Технический Университет им. И.Раззакова

Факультет информационных технологий

Кафедра ПОКС

Краткий курс лекции
«Дискретная математика»

(Для программистов)

Бишкек 2004
Cодержание
I. Основные элементы теории множеств

1.1 Понятия о множествах и его элементах . . . . . . . . . . . . . . . . . . . . . . . . . . 4

1.2 Операция над множествами . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5

1.3 Круги и диаграммы Эйлера . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6

1.4 Свойства операций над множествами . . . . . . . . . . . . . . . . . . . . . . . . . 7

1.5 Обобщение операций над множествами . . . . . . . . . . . . . . . . . . . . . . . . . . 8

1.6 Тождественные преобразования . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8

1.7 Доказательство равенств и тождеств между множествами . . . . . . . . . . . 9

1.8 Решение уравнений с множествами . . . . . . . . . . . . . . . . . . . . . . . . . 10

1.9 Символ и диаграмма Венна . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .11
I. Основные элементы теории множеств

1. Понятия о множествах и его элементах

Понятие множество относится к категорий одной из наиболее общих, основополагающих понятий математики. Однако, вместо строгого определения этого понятия обычно используется некоторое основное положение о множестве и его элементах.

Интуитивно под множеством понимается совокупность определенных вполне различаемых элементов. Основоположник теории множеств – немецкий математик Георг Кантор даёт следующее определение: Множество - это совокупность отдельных объектов составляющих одно целое.

Группа современных французских математиков выступающих под псевдонимом Н.Бурбаки исходит из такого определения: Множество образуется из элементов, обладающих некоторыми свойствами и находящихся в определенных отношениях между собой или с элементами других множеств.

Следует отметить что о множестве можно говорить тогда, когда его элементы различимы между собой. (например воду в некотором объме нельзя рассматривать как множество капель).

Для обозначения конкретного множество используется различные заглавные буквы

A, B, C ... или , иногда - с нижным индексом- A₁, A₂, A₃, ... , A_n.

Отдельные объекты, из которых состоит множество, называется элементами данного множества. Для их обозначения используется различные строчные буквы, либо строчные буквы с нижным индексом:

a, b, c или a₁, a₂, a₃,...., a_n.

Утверждение что множество состоит из различных элементов a₁, a₂, a₃,...., a_n записывается в виде:

A={a₁,a₂,a₃,…,a_n}.

Элементами множества могут быть не только отдельные объекты, но и множество каких либо других объектов. (Например: множество книг на полке, где каждая книга является элементом этого множества, а каждая книга есть множество страниц).

Принадлежность элемента к множества выражается символом : Записью a A обозначают, что a – есть элемент множества А, аналогично-a₁, a₂, a₃,...., a_n Aозначает,чтоa₁, a₂, a₃,...., a_n– элементы множесва А .

Отсутствие какого-то элемента в данном множества выражается символом или :

Запись b А или b А означает, что b не является элементом множества А (т.е.- во множестве А нет элемента b).

По количеству элементов множества разделяют на конечные и бесконечные. Среди бесконечных множеств выделяется счетное множество – это такое бесконечное множество, элементы которого возможно расположить в определенной последовательности, т.е.- перебрать их и/или перенумеровать. (Например - множество четных чисел).

Важное значение имеет понятие пустого множества, которое не содержит никаких элементов. Для его обозночения использует символ – Ø. Это понятие используется для определения не существующей совокупности элементов. (Например- множество зеленных слонов является примером пустого множества).

Множество, состоящее из всей совокупности допустимых элементов некоторого вида называют универсумом или основным (универсальным) множеством и обозначают символом U.

Множества А, все элементы которого принадлежат множеству В называется подмножеством (частью) множества В. Такое отношение между множествами называется включением и обозначается символом или . Запись А В или В А означает, что «множество А является подмножеством (частью) множества В» («множество А включено во множество В» или – «множество В включает/содержит множество А».

Математически (в символьном виде) данное понятие (отношение множеств А и В) записывается в виде:

Если x A => x B, то А В и наоборот: запись А В означает, что если x A то x B ,

(Символ (квантор) –означает “всякий”, “любой”, “все”, “каждый” и запись x – читается «любой (всякий, каждый)элемент x». Символ => (иногда →) - выражает отношение следования, т.е. – причинно-следственную связь двух фактов).

Наряду со строгим включением ( или ), которое исключает совпадение двух множеств,используется и отношение не строгого включения, выражаемое символом или .При этом запись А В означает, что множество А включено/содержится в В или совпадает с ним, т.е. отношение А В допускает и отношение тождественности (А=В). В соответствии с этим всякое множество можно рассматривать и как подмножество самого множества (А А).

Любое непустое множество А имеет по крайней мере два различных подмножества: А и Ø. Эти подмножества называются несобственными, а все другие подмножества А -называются собственным.

Множество, все элементы которого является подмножеством множества А, называют множеством подмножеств (множеством – степенью) А и обозначается (A).

Множество задается одним из двух способов:

1. 
   Если оно конечно, то внутри фигурных скобок { } записывается перечень всех элементов из которых оно состоит: А = {а_1, а₂, …, а_n}.
   
2. 
   Если же множество бесконечно, то оно задается определяющим свойством P(x), которым обладает каждый элемент (х) данного множества и записывается в виде .
   

А = { x| P(x) } или A = { x: P(x) }.

Р(х) – здесь, обычно, словесное утверждение об определяющем признаке (качествах, свойствах), характерном для всех элементов множества. Чаще всего это утверждение выражается в виде различных математических соотношений. В подобном случае множество записывается в виде:

Например: 1. А={множество людей| которые имеют фамилию Петров};

2. B={x| x²-4x+3=0}. (В данном случае будем иметь B = {1, 3}).
Два множества А и В считаются равными (тождественными) тогда и только тогда, когда все элементы множества А являются элементам множества В и наоборот. Математически это выражается записью А = В <=> A B и В А или, учитывая определение подмножества, – соотношением

А= В <=> 1) x A => x B и 2) х B => х A
2. Операция над множествами

1. 
   Объединением двух множеств А и В, обозначаемое в виде А В, называется множество, элементы которого входят хотя бы в одно из двух множеств - в А или в В :
   

А В = {x| x Aилиx B}.

2. 
   Пересечением двух множеств А и В, обозначаемое в виде А В, называется множество состоящее из всех элементов, входящих (одновременно) и в А, и в В :
   

А В={х| x А и х В}.

3. 
   Разностью двух множеств А и В, обозначаемое как А\В, называют множество состоящее из тех элементов А, которые не входят в В, т.е. -это та часть множества А, которая не входит в В:
   

А\В = {x|x Aи х В}.

4. 
   Дизьюктивной суммой или симметрической рахностью двух множеств (А и В), заисываемое в виде A+B (или- AB) называется множество, состоящее из тех элементов, которые входят только в А или только в В:
   

A+B (=AB) = {х| (х Aи х B) или (х Bи х A) }

С учетом понятия/обозначения разности двух множеств такую операцию можно записать и в виде –

AB ={ х| х А\В или х В\А }.

Пример: Пусть A = {1,2,3} иB = {2,3, 4}; тогда

A B = {1,2,3} {2,3, 4} = {1,2,3, 4}; A B = {1,2,3} {2,3, 4} = {2,3};

A\B = {1}; B\A = {4} и А+В = {1,2,3}+{2,3, 4} = {1, 4}.

5. 
   Дополнением множества А называется совокупность ( ) всех элементов универсума, не входящих во множество А, т.е.
   

={x| xєU и x A}=U\А.

6. 
   Дополнением множества А до В называется совокупность элементов В\А.
   

3. Круги и диаграммы Эйлера

Д 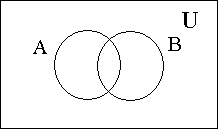ля наглядного представления (изображения) множеств и операций с ними используют диаграммы Эйлера, представляющая собой некоторую совокупность кругов, расположенных внутри прямоугольника в плоскости. При этом прямоугольником изображется универсум (U) , а любое подмножество этого универсума – в виде круга внутри прямоугольника. Точки прямоугольника – элементы универсума, а точки круга является элементами соответствующего множества:
Результаты выше указанных операций над некоторыми множествами А и В -множества с заштрихованными участками-будут представлены следующими диаграммами: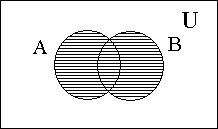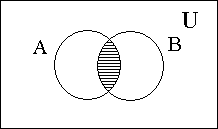




1) 2)

А 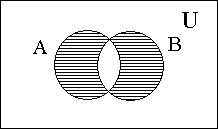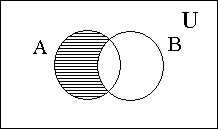В А∩В



3) 4)

А\В А+В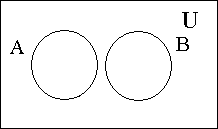





5)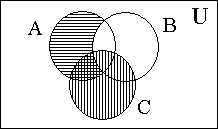
А∩В= Ø


= - А\B

|| - C


A B # - (А\В)∩С
4. Свойства операций над множествами

Указанные операции, как и различные операции других разделов математики, обладают рядом общих свойств:
1⁰ A B=B A; A B=B A – свойство коммутативности.

2⁰ A (B C)=(A B) C; A (B C)=(A B) C – свойство ассоциативности.

3⁰ A (B C)=(A B) (A C); A (B C)=(A B) (A C) – свойство

дистрибутивности.
Свойства пустого множества и уневерсума относительно операций и .

4⁰ A Ø =A; A U =A.

5⁰ A U = U; A Ø = Ø.

6⁰ A = U; A = Ø.

7⁰ = U; = Ø.

8⁰ A A=A; A A=A – закон идемпотентности.

9⁰ A (A B) = A; A (A B) = A – закон поглощения.

10⁰ = ; – теорема де Моргана.

К примеру диаграммы Эйлера к первому из соотношений 10⁰ имеют вид: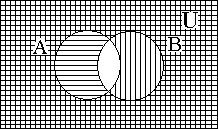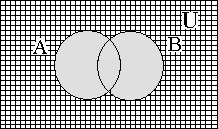




|| -
= -

# - # -
Все перечисленные выше свойства представленны парами двойственных (дуальных) отношений: одно из них следует из другого при замене операций на и наоборот на .

Соответствуюшие пары символов и а так же множества Ø и U называются дуальными.

При замене символов входяших в данные утверждения (соотношения) на дуальные мы получим новое предложение (соотношения), которое так же является утверждением. В этом заключается так называемый принцип двойственности или дуальности.

Кроме перечисленных свойств используется и следующие свойства операций дополнения (обозначаемое иногда символом ¬ ), \ , +, и равенства.

11⁰ Если А В= U и А В= Ø, то А= и В= .

12⁰ =U \А.

13⁰ =А.

14⁰ А\В=А .

15⁰ А+В=В+А.

16⁰ А+В=(А ) ( В ).

17⁰ (А+В)+С=А+(В+С).

18⁰ А+ Ø= Ø+А=А.

19⁰ А В <=> A B=A или- А В= В, или- А = Ø.

20⁰ А=В <=> (А ) ( В )= Ø или А+В= Ø.

Приведенные здесь свойства 11⁰ и 12⁰ не изменяется при замене символов дуальными, поэтому их называют самодвойственным.

Принцип дуальности можно распростронить и на операций \ и +, если использовать свойства 14⁰ и 15⁰.

Согласно свойству 19⁰ отношение А В можно записать как A B=A или же А В= В, но так как дуальным для A B=A является А В= A, то следовательно дуальным для А В следует считать отношение В А. Это означает, что относительно символа дуальным является противоположный символ и наборот.

Перечисленные 20 свойств различных операций со множествами используют для доказательства различных утверждений и соотношений между множествами, а также при выполнении тождественных преобразований и упрощении выражений, содержащих множества.
5. Обобщение операций над множествами

Из свойства комутативности следует, что объединить несколько множеств можно производить последовательно, не учитывая порядок следовония эти множеств; следовательно объеденение совокупности множеств можно выразить соотношением: А₁ А₂ ...... А_n= А_i - это есть, по определению операции объединения множеств, совокупность элементов, принадлежаших хотябы одному из перечисленных множеств А_i.
То же самое возможно и для пересечений этих множеств:

А₁ А₂ ...... А_n= А_i - это будет множеством элементов, принадлежаших (одновременно) всем множествам А_i.
Используя приведенные соотношения можно обобщить и другие соотношения, с операциями и/или .

Пример: Для теоремы де Моргана:

; .
6. Тождественные преобразования

Алгебра множеств представляет собой теоретико–множественный аналог обычной алгебры действительных чисел и основана на использовании перечисленных свойств операций над множествами.

Одним из разделов этой алгебры является тождественные преоброзования, с помощью которых можно упрощать или преобразовывать к удобному виду различные выражения содержашие множества.

Пример:

(A\ B) (B\A) = (A ) ( B) = (A ) (B ) = Ø

Путем таких преобразований (левой и/или правой частей уравнений и тождеств), в результате которых достигается максимальное упрощение заданного соотношения, доказывается (или отклоняется) справедливость заданных равенств и тождеств.

1. 
   Покажем, что имеет место равенство (А В С) ( С) ( С)=С :
   

(А В С) ( С) ( С) = (А В С) (С ( )) =

= С (( ) (А В)) = С (( ) (А В))=С U = С.

2. 
   (M\N) (N\M)=
   

M\N=M , N\M=N →

(M\N) (N\M)=(M ) (N )=(M ) (N ) = = .

Следует отметить, что любая теорема алгебры множеств (то есть любое тождество) выводится из первых пяти свойств операций над множеством путем подобных тождественных преобразований, а они – доказываются (прямым способом), исходя из отношения принадлежности .

7. Доказательство равенств и тождеств между множествами

Круги Эйлера можно использовать не только для наглядного изображения различных множеств и результатов операций над множеством в различных теоретико – множественных отношениях, но и для для проверки этих соотношений. Для этого расматривают выражения стоящие в правой и левой частях проверяемых соотношений; отдельно для каждого из них рисуют соответствующие диаграммы Эйлера и проверяют равны или неравны (заштрихованные) области диаграмм, соответствующие обеим частям заданного соотношения. При совпадении этих областей говорят, что данное соотношение справедливо.

Пример: А 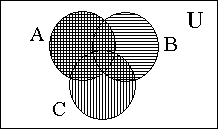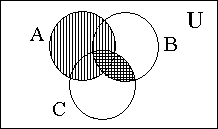(В С) = (А В) (А С)


= - В C = - А В

|| - A C

|| - А (В С) # - (А В) (А С)

Такой способ является самым простым способом проверки справедливости заданных соотношений.

Другой (прямой) способ доказательства равенств и тождеств, содержащих множества с различными операциями, основывается на доказательстве 2-х положений: