Задача о диете (упрощенный вариант). Лекции Задачи оптимизации при принятии решений

• Название: Лекции Задачи оптимизации при принятии решений
• Анкор: Задача о диете (упрощенный вариант)
• Дата: 03.06.2022
• Размер: 441.46 Kb.
• Имя файла: Zadanie2.docx
• Тип: Лекции; #566651
• страница: 2 из 3

Задания

1. Изобразите на плоскости ограничения задачи линейного программирования и решите (графически) эту задачу:

400W₁ + 450W₂ min

5W₁ + 10W₂ ≥ 45

20W₁ + 15W₂ ≥ 80

W₁ ≥ 0, W₂ ≥ 0
РЕШЕНИЕ:
Каждое неравенство исходной системы ограничений определяет полуплоскость. Запишем уравнения граничных прямых для этих полуплоскостей.

(1) 5W₁ + 10W₂ = 45 (2) 20W₁ + 15W₂ = 80

W1	0	9		W1	0	4
W2	4,5	0		W2	5,3	0

Построим прямые по данным двум точкам.

Каждая прямая разбивает плоскость на две полуплоскости. Для выбора полуплоскостей, определяемых каждым неравенством, подставим координаты «пробной» точки (0;0) в каждое неравенство. Получаем:

50+10045 не верно. Следовательно, отмечаем полуплоскость, не содержащую «пробную» точку (0;0), таким образом, допустимые значения параметров лежат выше прямой (1) или на ней.

200+15080 не верно. Следовательно, отмечаем полуплоскость, не содержащую «пробную» точку (0;0), т.е. допустимые значения параметров лежат выше прямой (2) или на ней.

Найдем пересечение отмеченных полуплоскостей с учетом условия: W1, W2  0. Следовательно, область допустимых значений параметров (W1, W2) является неограниченной сверху.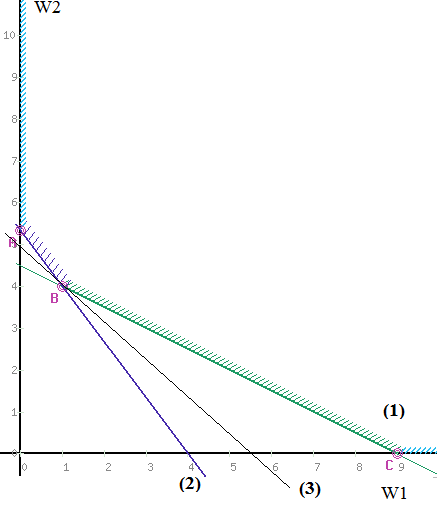



Рисунок 1 – Область допустимых значений
Минимум целевой функции 400W₁ + 450W₂ может достигаться только в вершинах этого "многоугольника". Вершин всего три – это А, В и С.

Найдем координаты точки В, как точку пересечения двух прямых (1) и (2). Для этого решим систему:

5W₁ + 10W₂ = 45

20W₁ + 15W₂ = 80,

Первое уравнение умножим на 4 и вычтем второе, получим

40W₂ – 15W₂ = 180 – 80

25W₂ = 100

W₂ = 4.

Подставим полученное значение в первое уравнение, найдем W₁ = 1.

Итак, В = (1,4).

Прямая (3) на рис. 1 - это прямая, соответствующая целевой функции 400W₁ + 450W₂. Она проходит между прямыми (1) и (2), задающими ограничения, и минимум достигается в точке В, через которую и проходит прямая (3). Следовательно

2. Решите задачу линейного программирования:

W₁ + 5W₂ max

0,1W₁ + W₂ ≤ 3,8

0,25W₁ + 0,25W₂ ≤ 4,2

W₁ ≥ 0, W₂ ≥ 0
РЕШЕНИЕ:
Решим задачу линейного программирования средствами MS Excel.

Сначала определим ячейки, в которые будет помещен результат решения. Пусть это будут ячейки В2, С2, сделаем у них заголовки. В этих ячейках нет данных, их должен будет рассчитать Excel, они выделены цветом. Далее заполним коэффициенты при неизвестных и правые части системы ограничений. Заведем строку для целевой функции. Цветом выделена ячейка, в которой будет находиться значение целевой функции для найденного оптимального решения.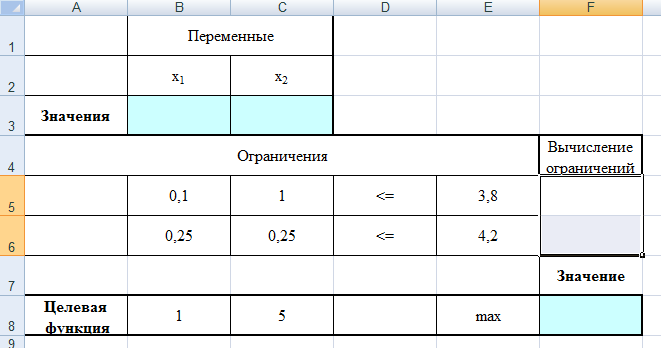


В ячейки D5, D6 введем формулы для зависимостей левых частей системы ограничений, а в ячейку E8 – формулу для зависимости целевой функции.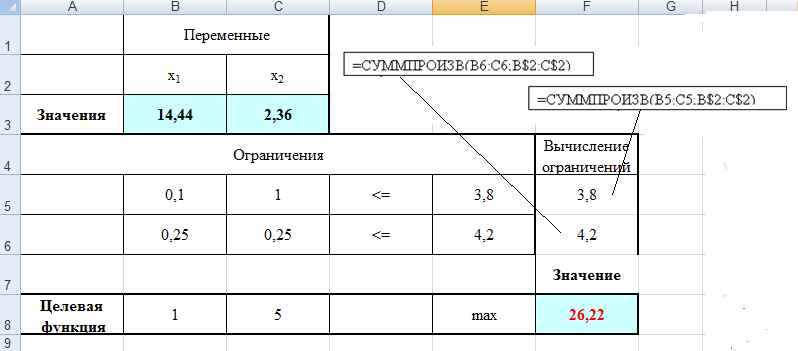



Далее необходимо воспользоваться надстройкой Поиск решения. На вкладке Данные в группе Анализ выберем команду Поиск решения. Появится диалоговое окно Поиск решения, которое необходимо заполнить следующим образом (для добавления ограничений пользуемся кнопкой Добавить):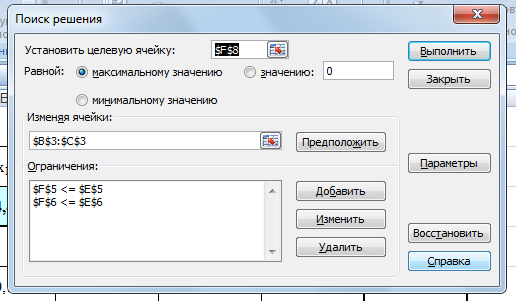



Далее нажимаем кнопку Параметры и в появившемся окне Параметры поиска решений устанавливаем флажок неотрицательные значения, линейная модель и нажимаем OK.



В окне Поиск решения после нажатия кнопки Выполнить появляется окно Результаты поиска решения, в котором выбираем сохранение найденных значений и нажимаем кнопку ОК.



Результаты поиска решений (для ячеек В2 и С2 установлены числовые форматы с 0 знаками после запятой):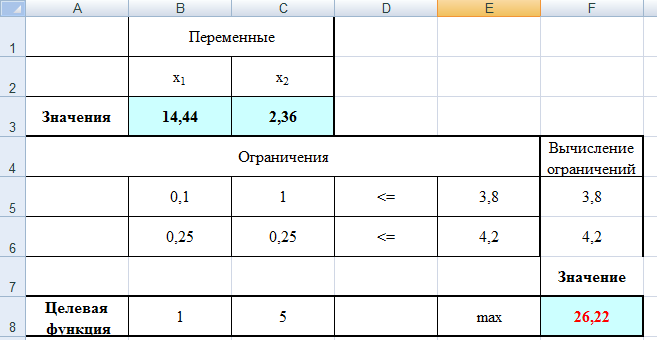



Получили .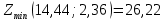
3. Решите задачу целочисленного программирования:

10X + 5Ymax

8X + 3Y ≤ 40

3X +10Y ≤ 30

X ≥ 0, Y ≥ 0

XиY - целые числа
РЕШЕНИЕ:
Данную задачу можно решить также средствами MS Excel, как и задачу №2, введя дополнительное условие о целочисленности значений.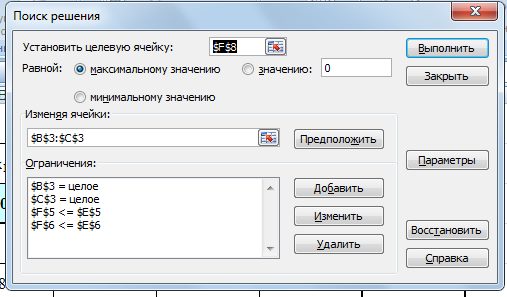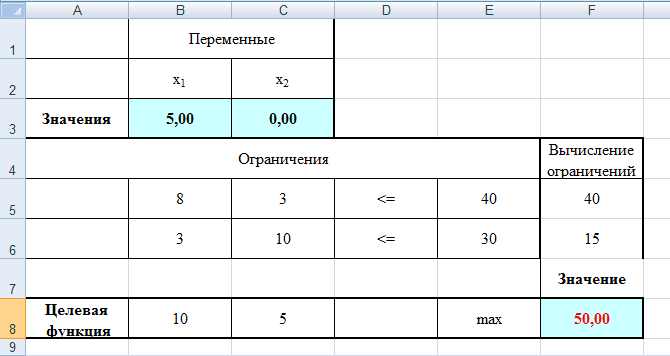





Получили .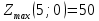
4. Решите задачу о ранце:

X₁ + X₂ + 2X₃ + 2X₄ + X₅ + X₆ max

0,5X₁ + X₂ + 1,5X₃ + 2X₄ + 2,5X₅ + 3X₆ ≤ 3

Управляющие параметры X_k, k=1,2,3,4,5,6, принимают значения из множества, содержащего два элемента - 0 и 1.
РЕШЕНИЕ:
Имеется 6 предметов, для каждого из них необходимо решить, класть его в ранец или не класть. При этом Хk = 1, если предмет размещают в ранце, и Хk = 0, если нет, k = 1,2,…, n.

Максимально возможная вместимость ранца В = 3.

Предмет	1	2	3	4	5	6
Вес k-го предмета (Ai)	0,5	1	1,5	2	2,5	3
Полезность (стоимость) k-го предмета (Ci)	1	1	2	2	1	1

Задачу о ранце можно решить методом перебора с помощью средств MS Excel.

Для этого необходимо воспользоваться надстройкой Поиск решения. На вкладке Данные в группе Анализ выберем команду Поиск решения. Появится диалоговое окно Поиск решения, которое необходимо заполнить следующим образом (для добавления ограничений пользуемся кнопкой Добавить):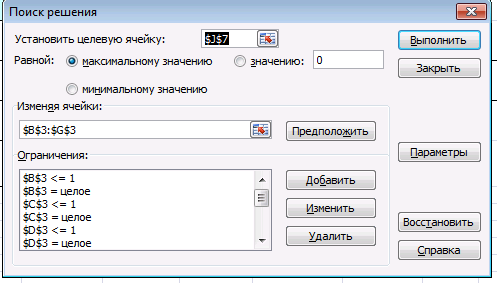



Вводим ограничение по весу.

На каждую переменную нужно добавить также ограничения по целочисленности и x_k<=1, так как x_k принимают значения либо 0, либо 1 по условию задачи.

После выполнения поиска решения, получаем: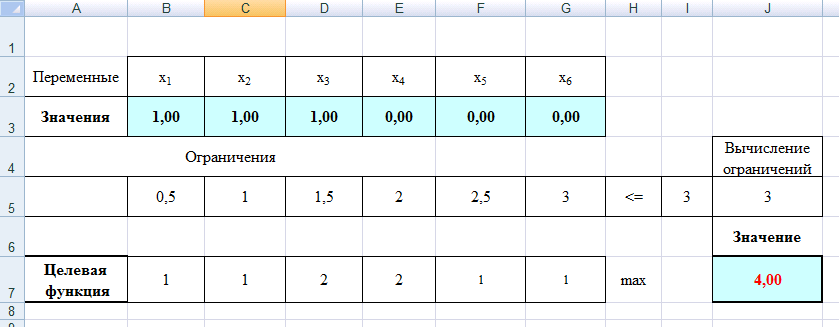



Таким образом, максимальная полезность будет получена, если в ранец поместить первый, второй и третий предмет, максимальная полезность при этом будет равна 4.
5. Транспортная сеть (с указанием расстояний) приведена на рис. 8.9. Найдите кратчайший путь из пункта 1 в пункт 4.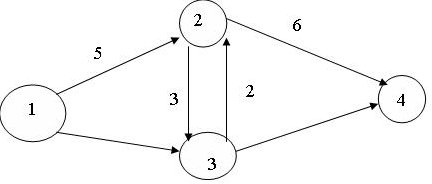




Рис. 8.9. Исходные данные к задаче о кратчайшем пути
РЕШЕНИЕ:
Введем обозначение: С(Т) - длина кратчайшего пути из вершины 1 в вершину Т. (Поскольку любой путь, который надо рассмотреть, состоит из дуг, а дуг конечное число, и каждая входит не более одного раза, то претендентов на кратчайший путь конечное число, и минимум из конечного числа элементов всегда достигается.) Рассматриваемая задача состоит в вычислении С(4) и указании пути, на котором этот минимум достигается.

В вершину 4 можно попасть либо из вершины 2, пройдя путь, равный 6, либо из вершины 3, пройдя путь, равный 8. Поэтому справедливо соотношение: C(4)=min{C(2)+6;C(3)+8}.

Таким образом, проведена реструктуризация (упрощение) задачи – нахождение C(4) сведено к нахождению C(2) и C(3).

В вершину 2 можно попасть либо из вершины 1, пройдя путь, равный 5, либо из вершины 3, пройдя путь, равный 2, либо из вершины 1, пройдя путь равный 6 (4+2). Поэтому справедливо соотношение: C(2)=min{C(1)+5;C(3)+2;С(1)+С(3)+2}. Так как путь из вершины 1 в вершину 2 через вершину 3 получается длиннее на 1 ед., то не будем рассматривать данный вариант. Очевидно, что C(1)=0. Поэтому получим: C(2)=min{5;C(3)+2} = 5.

В вершину 3 можно попасть либо из вершины 1, пройдя путь, равный 4, либо из вершины 2, пройдя путь, равный 3, либо из вершины 1, пройдя путь равный 8 (5+3). Так как путь из вершины 1 в вершину 3 через вершину 2 получается длиннее на 1 ед., то не будем рассматривать данный вариант. Поэтому справедливо соотношение: C(3)=min{C(1)+4;C(2)+3; С(1) + C(3)+3} = 4.

Тогда C(4)=min{C(2)+6;C(3)+8}= min{5+6;4+8}= min{11;12}= 11.

Таким образом, длина кратчайшего пути равна 11. Итак, кратчайший путь таков: 1  2  4.
6. Как послать максимальное количество грузов из начального пункта 1 в конечный пункт 8, если пропускная способность путей между пунктами транспортной сети (рис. 8.10) ограничена (табл. 8.7)?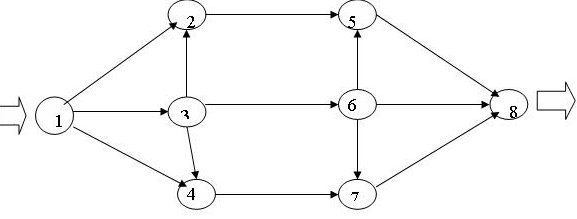




Рис. 8.10. Транспортная сеть к задаче о максимальном потоке
Таблица 8.7

Исходные данные к задаче о максимальном потоке

Пункт отправления	Пункт назначения	Пропускная способность
1	2	1
1	3	2
1	4	3
2	5	2
3	2	2
3	4	2
3	6	1
4	7	4
5	8	3
6	5	2
6	7	1
6	8	1
7	8	3

РЕШЕНИЕ:
Дадим формулировку задачи о максимальном потоке в терминах линейного программирования. Пусть Х_KM - объем перевозок из пункта К в пункт М. Согласно рис. 8.10 K=1,2,3,4,5,6,7 М=2,3,4,5,6,7,8. Всего имеется 13 переменных X_KM, а именно, X₁₂, X₁₃, X₁₄, X₂₅, X₃₂, X₃₄, X₃₆, X₄₇, X₅₈, X₆₅, X₆₇, X₆₈, X₇₈. Задача линейного программирования, нацеленная на максимизацию потока, имеет вид:

Fmax, X₁₂ + X₁₃ + X₁₄ = F (0)

-X₁₂-X₃₂+X₂₅=0 (1)

-X₁₃+X₃₂+X₃₆+X₃₄=0 (2)

-X₁₄-X₃₄+X₄₇=0 (3)

-X₂₅-X₆₅+X₅₈=0 (4)

-X₃₆+X₆₅+X₆₈+X₆₇=0 (5)

-X₄₇-X₆₇+X₇₈=0 (6)

-X₅₈-X₆₈-X₇₈= -F (7)

X₁₂≤1

X₁₃≤2

X₁₄ ≤ 3

X₂₅ ≤ 2

X₃₂≤ 2

X₃₄ ≤ 2

X₃₆ ≤ 1

X₄₇ ≤ 4

X₅₈ ≤ 3

X₆₅ ≤ 2

X₆₇ ≤ 1

X₆₈ ≤ 1

X₇₈ ≤ 3

Х_KM≥ 0, K=1,2,3,4,5,6,7 М=2,3,4,5,6,7,8.

F ≥ 0

Здесь F- целевая функция, условие (0) описывает вхождение грузов в транспортную систему. Условия (1) - (6) задают балансовые соотношения для узлов 2-7 системы. Другими словами, для каждого из внутренних узлов входящий поток грузов равен выходящему потоку, грузы не скапливаются внутри системы и не "рождаются" в ней. Условие (7) - это условие "выхода" грузов из системы. Вместе с условием (1) оно составляет балансовое соотношение для системы в целом ("вход" равен "выходу"). Следующие 13 неравенств задают ограничения на пропускную способность отдельных "веток" транспортной системы. Затем в системе ограничений задачи линейного программирования указана неотрицательность объемов перевозок и целевой функции. Ясно, что последнее неравенство вытекает из вида целевой функции (соотношения (1) или (7)) и неотрицательности объемов перевозок. Однако последнее неравенство несет некоторую общую информацию - через систему может быть пропущен либо положительный объем грузов, либо нулевой (например, если внутри системы происходит движение по кругу), но не отрицательный (он не имеет экономического смысла, но формальная математическая модель об этом "не знает").

Решение данной задачи найдем с помощью средств MS Excel.

Для этого необходимо воспользоваться надстройкой Поиск решения. На вкладке Данные в группе Анализ выберем команду Поиск решения. Появится диалоговое окно Поиск решения, которое необходимо заполнить следующим образом (для добавления ограничений пользуемся кнопкой Добавить):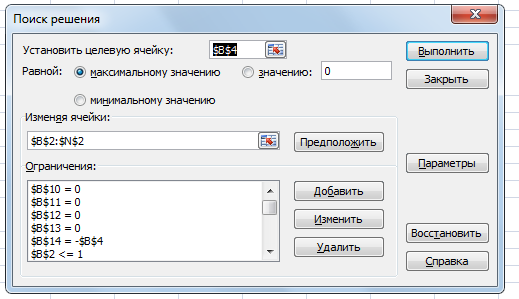



Продолжение ограничений: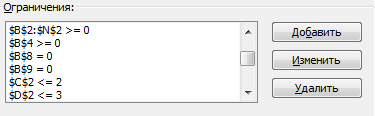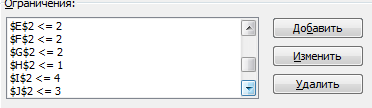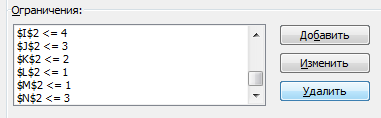







Получили решение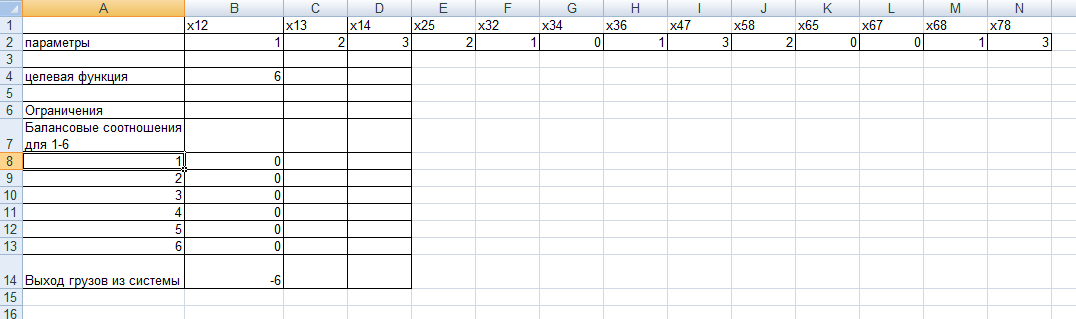



Решение можно представить в виде таблицы: