ить. практикум 3н. Функции распределения. Лекционный материал по данной теме см в лекции 3
 Скачать 265.14 Kb. Скачать 265.14 Kb.
|
|
Лекционный материал по данной теме см. в лекции 3. Понятие случайной величины (с.в.)является основным понятием теории вероятностей. Если множество значений случайной величины содержит целый отрезок числовой оси, то такие случайные величины называют непрерывными. Интегральной функцией распределения непрерывной с.в.  называется функция называется функция 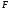 переменной переменной , выражающая вероятность того, что , выражающая вероятность того, что в результате испытания примет значение, меньшее, чем в результате испытания примет значение, меньшее, чем   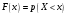 (1) (1)Пусть задана интегральная функция распределения вероятности . 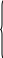 Дано 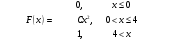 Требуется : Найти плотность вероятности 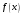 ; ;Построить графики 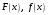 ; ;Найти 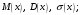 Найти 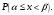  Решение. По определению 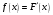 в точках, где в точках, где  существует существует  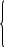  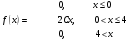 Для определения 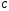 воспользуемся правилом воспользуемся правилом 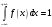 . Отсюда . Отсюда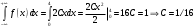 . И поэтому . И поэтому 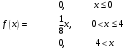  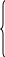 ; ; 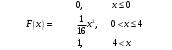 Строим графики функций 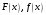 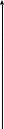   1   4 Г  рафик рафик 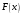   0,5 0,5    4 4График 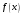 Определяем числовые характеристики непрерывных с.в. Математическое ожидание 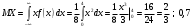 Дисперсию 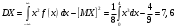 Среднее квадратическое отклонение 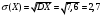 Найдем вероятность попадания с.в. в интервал (1;3)  Пусть задана дифференциальная функция (плотность) распределения вероятности. Д 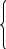 ано ано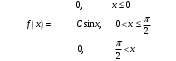 Требуется : Найти плотность вероятности 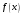 ; ;Найти 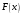 , построить графики , построить графики 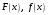 ; ;Найти 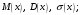 Найти 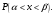 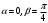 Решение. Чтобы найти 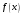 нужно определить постоянную нужно определить постоянную 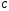 из условия из условия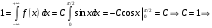   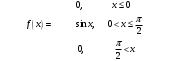 Определяем интегральную функцию 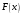 : :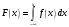 При 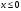 имеем имеем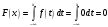 При 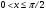 имеем имеем  При 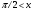 имеем имеем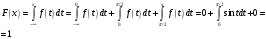 Отсюда 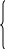 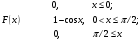 Строим график 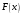     1   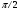 График 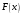 Строим график 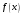   1 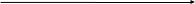   График 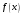 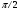 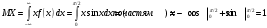 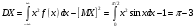 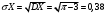 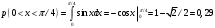 Далее рассматриваем нормальное распределение случайной величины. Нормальное распределение играет исключительно важную роль в приложениях теории вероятностей к практическим задачам Нахождение вероятности по интервалу. Пример 1.Пусть параметры, закладываемые на временное формирование поездов, подчиняются нормальному закону распределения с параметрами МХ=120мин, 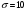 мин. Что более вероятно: время формирования поезда от80 до 100 или от120 до 150 мин? мин. Что более вероятно: время формирования поезда от80 до 100 или от120 до 150 мин?Решение. Обозначим случайную величину через Х- (время формирования поезда). Эта случайная величина распределена по нормальному закону. 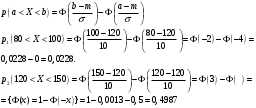 Обозначения: 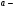 математическое ожидание случайной величины математическое ожидание случайной величины  распределённой по нормальному закону. распределённой по нормальному закону. 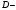 дисперсия случайной величины дисперсия случайной величины  распределённой по нормальному закону. распределённой по нормальному закону. 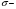 среднеквадратичное отклонение среднеквадратичное отклонение 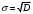 . . Пример 2. Пусть случайная величина  распределена по нормальному закону (см. лекцию3 формулу(8)). Параметры распределения заданы распределена по нормальному закону (см. лекцию3 формулу(8)). Параметры распределения заданы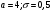 . Найти вероятность того, что . Найти вероятность того, что  примет значение в интервале примет значение в интервале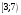 . . Решение. Согласно формуле (11) см. лекцию 3 имеет место 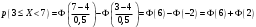 По таблице значений функции 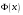 находим находим 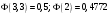 Отсюда 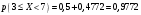 Пример 3. Пусть случайная величина  распределена по нормальному закону (см. лекцию3 формулу(8)). Параметры распределения заданы распределена по нормальному закону (см. лекцию3 формулу(8)). Параметры распределения заданы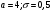 . Найти вероятность того, что . Найти вероятность того, что  примет значение в интервале примет значение в интервале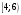 . . Решение. Согласно формуле (11) см. лекцию 3 имеет место 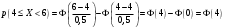 По таблице значений функции 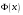 находим находим 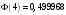 Отсюда 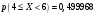 Пример 4. Пусть случайная величина  распределена по нормальному закону (см. лекцию3 формулу(8)). Параметры распределения заданы распределена по нормальному закону (см. лекцию3 формулу(8)). Параметры распределения заданы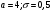 . Найти вероятность того, что . Найти вероятность того, что  примет значение в интервале примет значение в интервале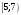 . . Решение. Согласно формуле (11) см. лекцию 3 имеет место 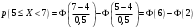 По таблице значений функции 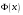 находим находим 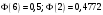 Отсюда 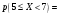 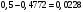 Пример 5. Пусть случайная величина  распределена по нормальному закону (см. лекцию 3 формулу(8)). Параметры распределения заданы распределена по нормальному закону (см. лекцию 3 формулу(8)). Параметры распределения заданы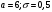 . Найти вероятность того, что . Найти вероятность того, что  примет значение в интервале примет значение в интервале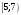 Решение. Согласно формуле (11) см. лекцию3 имеет место 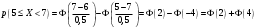 По таблице значений функции 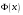 находим находим 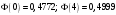 Отсюда 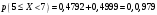 . . Пример 6. Пусть случайная величина  распределена по нормальному закону (см. лекцию 3 формулу(8)). Параметры распределения заданы распределена по нормальному закону (см. лекцию 3 формулу(8)). Параметры распределения заданы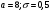 . Найти вероятность того, что . Найти вероятность того, что  примет значение в интервале примет значение в интервале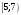 Решение. Согласно формуле (11) см. лекцию3 имеет место 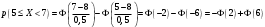 По таблице значений функции 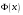 находим находим 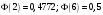 Отсюда 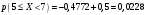 Нахождение интервала по вероятности нормально распределённой случайной величины. Пример 7. 1) Применяем формулу  из лекции 3. Длина изготавливаемой автоматом детали нормальная случайная величина Х С параметрами из лекции 3. Длина изготавливаемой автоматом детали нормальная случайная величина Х С параметрами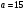 см и см и 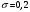 см. Найти вероятность брака, если допускаемые размеры детали должны быть см. Найти вероятность брака, если допускаемые размеры детали должны быть 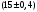 см. Какой диапазон длины деталей можно гарантировать с вероятностью 0,8? см. Какой диапазон длины деталей можно гарантировать с вероятностью 0,8?Решение. Найдем вероятность того, что деталь не является бракованной, то есть 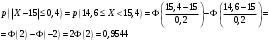 Тогда противоположное событие это вероятность брака. Она равна 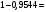 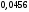 . .2). Для вычисления диапазона длины деталей, который можно гарантировать с вероятностью 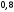 , применяем формулу , применяем формулу из лекции 3. Из условия задачи имеем: из лекции 3. Из условия задачи имеем: 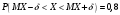 По формуле (12) о вероятности отклонения случайной величины По формуле (12) о вероятности отклонения случайной величины  от математического ожидания получим от математического ожидания получим 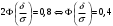 .Тогда, по таблице значений функции .Тогда, по таблице значений функции получаем получаем 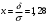 . По условию . По условию Ответ. Вероятность получения бракованной детали равна 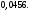 С вероятностью 0,8 можно гарантировать диапазон длины деталей С вероятностью 0,8 можно гарантировать диапазон длины деталей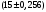 см. Это означает, что 20% деталей будут иметь отклонения от стандартной длины см. Это означает, что 20% деталей будут иметь отклонения от стандартной длины 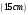 больше чем больше чем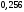 . . Пример 8. Случайная величина  распределена по нормальному закону. Математическое ожидание случайной величины распределена по нормальному закону. Математическое ожидание случайной величины  : : 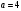 см. Дисперсия случайной величины см. Дисперсия случайной величины : :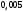 см. Какой интервал распределения случайной величины можно гарантировать с вероятностью см. Какой интервал распределения случайной величины можно гарантировать с вероятностью  . . Решение. Определяем среднее квадратическое отклонение  случайной величины случайной величины  : :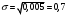 . Применяем формулу (12) из лекции 3 . Применяем формулу (12) из лекции 3  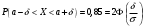 . Следовательно . Следовательно . Откуда ,по таблице значений функции . Откуда ,по таблице значений функции получаем получаем 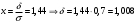 .С вероятностью .С вероятностью  можно гарантировать интервал можно гарантировать интервал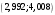 . . Пример 9. Диаметр вала – случайная величина  , распределённая по нормальному закону , распределённая по нормальному закону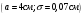 . В каких границах следует ожидать диаметры валов при их массовой закупке, чтобы вероятность их нахождения в этих границах была равна 0,98. . В каких границах следует ожидать диаметры валов при их массовой закупке, чтобы вероятность их нахождения в этих границах была равна 0,98.Решение. Применяем (12) из лекции 3  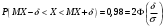 . Следовательно . Следовательно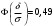 . Откуда ,по таблице значений функции . Откуда ,по таблице значений функции получаем получаем 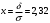 и и 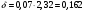 . .Ожидаемые границы валов 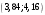 . . Пример 10. Автомат изготовляет шарики. Шарик стандартный, если отклонение  диаметра шарика от проектного размера по абсолютной величине меньше диаметра шарика от проектного размера по абсолютной величине меньше 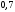 мм. Считается, что случайная величина мм. Считается, что случайная величина  распределена по нормальному закону с параметрами распределена по нормальному закону с параметрами 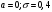 мм. Найти сколько в среднем будет стандартных шариков из ста заготовленных. мм. Найти сколько в среднем будет стандартных шариков из ста заготовленных.Решение. Из условия задачи следует: 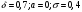 . Применяем формулу (12) из третьей лекции : . Применяем формулу (12) из третьей лекции :  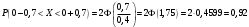 . Следовательно, вероятность отклонения от проектного размера шарика на величину меньшую чем . Следовательно, вероятность отклонения от проектного размера шарика на величину меньшую чем 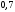 равна равна 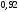 Вывод. Примерно Вывод. Примерно 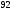 шарика из каждой сотни будут стандартными. шарика из каждой сотни будут стандартными. Домашнее задание. Задачи из ИДЗ. № 6,7,8 |
