Лекция 14 ЭВМ. Исследование монотонности, экстремумов функции с помощью производной

• Название: Исследование монотонности, экстремумов функции с помощью производной
• Дата: 06.12.2021
• Размер: 131.5 Kb.
• Имя файла: Лекция 14 ЭВМ.doc
• Тип: Исследование; #293718

Лекция 14. Исследование монотонности, экстремумов функции с помощью производной.

Монотонность функции. Точки экстремума и экстремумы функции

Рассмотрим некоторую функцию  .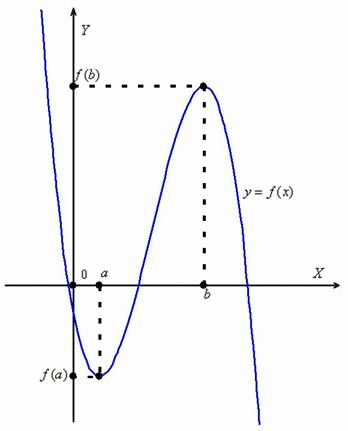

 

                                 Функция возрастает на интервале, если для любых двух точек этого интервала, связанных отношением  , справедливо неравенство  . То есть, бОльшему значению аргумента соответствует бОльшее значение функции, и её график идёт «снизу вверх». Демонстрационная функция   растёт на интервале  .

Аналогично, функция убывает на интервале, если для любых двух точек данного интервала, таких, что  , справедливо неравенство  . То есть, бОльшему значению аргумента соответствует мЕньшее значение функции, и её график идёт «сверху вниз». Наша функция   убывает на интервалах  .

Если функция возрастает или убывает на интервале, то её называют строго монотонной на данном интервале. Что такое монотонность? Понимайте в буквальном смысле – однообразие.

Точка   называется точкой максимума, если существует её окрестность, такая, чтодля всех значений   данной окрестности выполнено неравенство  . 
Точка   называется точкой минимума, если существует её окрестность, такая, чтодля всех значений   данной окрестности выполнено неравенство  .

– значение   называют максимумом функции;
– значение   называют минимумом функции.

Общее название – экстремумы функции.

Точки экстремума – это «иксовые» значения.
Экстремумы – «игрековые» значения.

Рассмотрим  на некотором интервале функцию  . Тогда:

– если производная   на интервале, то функция   возрастает на данном интервале;

– если производная   на интервале, то функция   убывает на данном интервале.

Примечание: справедливы и обратные утверждения.

первое достаточное условие экстремума,

пусть функция дифференцируема в некоторой окрестности критической точки  . Тогда:

– если при переходе через точку   производная меняет знак с «плюса» на «минус», то в данной точке функция достигает максимума;

– если при переходе через точку   производная меняет знак с «минуса» на «плюс», то в данной точке функция достигает минимума

На основании вышесказанного формулируют правило исследования функции на монотонность,экстремум в виде следующего алгоритма:

1.найти производную данной функции

2.найти её производную

3.найти критические точки(те,в которых производная равна 0,либо не существует)

4.нанести критические точки на числовую прямую

5.на каждом из полученных интервалов отметить знак производной

6.интервалы,на которых производная имеет +, будут интервалами возрастания функции и убывания в случае –

7.точки числовой прямой,в которых производная существует и меняет знак,будут точками экстремума функции:max, если с + на- ,и min,если с – на +

Задание. Исследовать функцию   на монотонность на всей числовой прямой.

Решение. Найдем производную заданной функции:



Для любого действительного  :  , а поэтому делаем вывод, что заданная функция возрастает на всей действительной оси.

Ответ. Функция   возрастает на всей действительной оси.

Задание. Исследовать функцию   на экстремум.

Решение. Находим производную заданной функции:



Далее ищем критические точки функции, для этого решаем уравнение  :



Первая производная определена во всех точках. Таким образом, имеем одну критическую точку  . Наносим эту точку на координатную прямую и исследуем знак производной слева и справа от этой точки (для этого из каждого промежутка берем произвольное значение и находим значение производной в выбранной точке, определяем знак полученной величины):



Так как при переходе через точку   производная сменила свой знак с "-" на "+", то в этой точке функция достигает минимума (или минимального значения), причем  .

Ответ.