Шпора по Граничным условиям. Лекция 04. Лекция 04 Первое уравнение Максвелла
 Скачать 262.38 Kb. Скачать 262.38 Kb.
|
|
Лекция 04 Первое уравнение Максвелла Рассмотрим первое уравнение Максвелла. 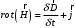 Смысл членов его в правой части легче понять, рассматривая их проявление раздельно. Если электромагнитный процесс неизменен во времени ( 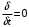 ), или, как говорят, стационарен, то уравнение принимает вид: ), или, как говорят, стационарен, то уравнение принимает вид: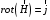 где 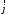 в данном случае – плотность постоянного тока. Первое уравнение Максвелла характеризует при этом связь магнитного поля и постоянного тока. Нельзя представить себе постоянный ток без магнитного поля, поскольку в данном случае – плотность постоянного тока. Первое уравнение Максвелла характеризует при этом связь магнитного поля и постоянного тока. Нельзя представить себе постоянный ток без магнитного поля, поскольку 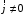 , обязательно при , обязательно при 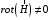 . .Если же поле изменяется во времени ( 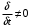 ), но ток проводимости отсутствует ( ), но ток проводимости отсутствует (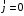 ), то: ), то: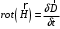 . .Сравнивая это уравнение с предыдущим, видим, что векторная функция 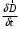 , выражающая скорость изменения электрической индукции, играет во втором случае ту же роль, что плотность тока проводимости в первом, т.е. существование изменений во времени индукции , выражающая скорость изменения электрической индукции, играет во втором случае ту же роль, что плотность тока проводимости в первом, т.е. существование изменений во времени индукции 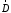 влечет за собой наличие магнитного поля влечет за собой наличие магнитного поля 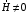 . Величина . Величина 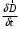 называется плотностью тока смещения. называется плотностью тока смещения.Подобно тому, как это делалось при рассмотрении второго уравнения Максвелла, получим первое уравнение Максвелла в интегральной форме. Проведя интегрирования по поверхности S: 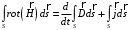 . .Применяя теорему Стокса для левой части уравнения: 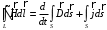 . .Интеграл 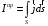 выражает поток вектора выражает поток вектора 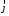 через поверхность S и, следовательно, является током проводимости, пересекающим эту поверхность. через поверхность S и, следовательно, является током проводимости, пересекающим эту поверхность. Аналогично, 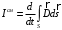 выражает ток смещения. Полным током и соответственно плотностью полного тока называются величины: выражает ток смещения. Полным током и соответственно плотностью полного тока называются величины: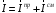 ; ; 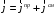 . .Итак, согласно первому уравнению Максвелла в интегральной форме, циркуляция напряженности магнитного поля 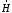 по произвольному контуру L равна полному току через любую поверхность S опирающуюся на этот контур. по произвольному контуру L равна полному току через любую поверхность S опирающуюся на этот контур.Из уравнения видно, что в отсутствии магнитного поля равен нулю и полный ток ( 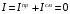 ). Но появление тока ( ). Но появление тока (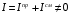 ) обязательно порождает магнитное поле: ) обязательно порождает магнитное поле: 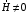 , поскольку должна быть отлична от нуля и левая часть. Согласно первому уравнению Максвелла, роли тока проводимости и тока смещения при этом совершенно одинаковы: магнитное поле может возбуждаться как током проводимости, так и током смещения, т.е. изменением потока электрической индукции. , поскольку должна быть отлична от нуля и левая часть. Согласно первому уравнению Максвелла, роли тока проводимости и тока смещения при этом совершенно одинаковы: магнитное поле может возбуждаться как током проводимости, так и током смещения, т.е. изменением потока электрической индукции.Ток смещения – одна из характеристик переменного электромагнитного поля. О нем мы будем говорить еще не раз. Пока же рассмотрим одно из свойств полного тока, подчеркивающее роль тока смещения в ряде важных случаев. Свойство полного тока. Применяя операцию дивергенции к левой и правой частям первого уравнения Максвелла, слева, в соответствии с 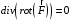 имеем нуль, так что: имеем нуль, так что: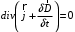 Т.е. расходимость вектора плотности полного тока равна нулю, а это, как известно, значит, что линии этого вектора непрерывны. Плотность тока проводимости, таким свойством не обладает и линии этого вектора могут обрываться, но тогда тут же начинаются линии вектора плотности тока смещения. 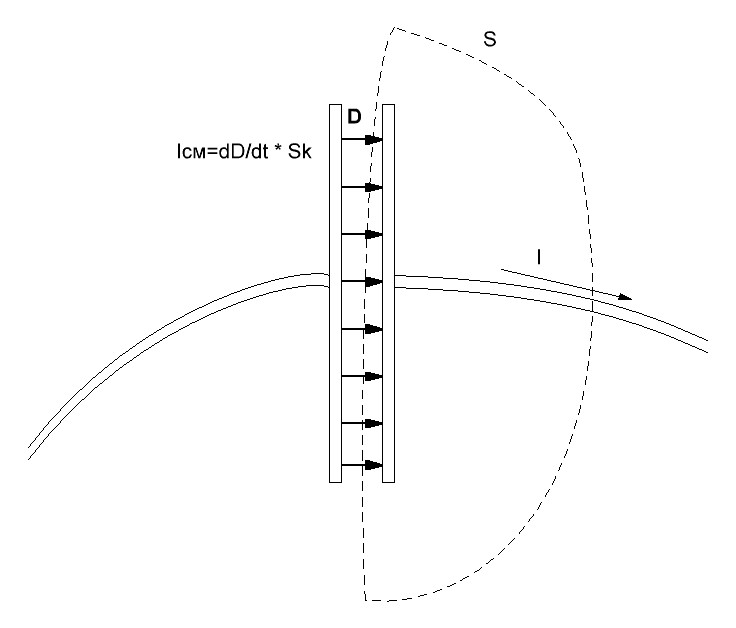 Рис. 2.2 из Никольского Возьмем некоторую замкнутую поверхность 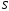 , ограничивающую объем , ограничивающую объем 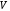 . Произведя в . Произведя в 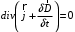 интегрирование по интегрирование по 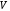 и применив теорему Остроградского-Гаусса получаем: и применив теорему Остроградского-Гаусса получаем: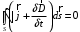 или или 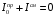 Где индекс 0 означает, что речь идет о токах, пересекающих замкнутую поверхность (положителен ток, выходящий из поверхности). Как видно, полный ток, через какую-либо замкнутую поверхность 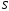 равен нулю – выходящий ток равен входящему. равен нулю – выходящий ток равен входящему.Поясним полученный результат на примере конденсатора в цепи переменного тока. Замкнутая поверхность S (она показана пунктиром) проведена так, что проходя между пластинами конденсатора она затем пересекает провод. Очевидно, только в этом месте через поверхность S проходит ток проводимости I. Он уравновешивается входящим внутрь S током смещения 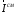 , который практически сосредоточен внутри конденсатора. Считая, что электрическое поле внутри конденсатора однородно ( , который практически сосредоточен внутри конденсатора. Считая, что электрическое поле внутри конденсатора однородно (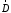 везде имеет одну и ту же величину), а, следовательно, неизменна в пространстве и плотность тока смещения везде имеет одну и ту же величину), а, следовательно, неизменна в пространстве и плотность тока смещения 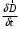 , имеем: , имеем: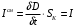 , ,где 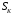 - площадь пластины конденсатора. Если - площадь пластины конденсатора. Если 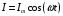 (гармоническое колебание), то: (гармоническое колебание), то: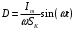 . .В случае воздушной среды с высокой точностью справедливы соотношения 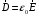 , поэтому абсолютное значение электрического поля в конденсаторе равно: , поэтому абсолютное значение электрического поля в конденсаторе равно: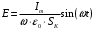 . .Магнитное поле прямолинейного тока Рассмотрим простой пример расчета магнитного поля на основании первого уравнения Максвелла. Известно, что магнитные силовые линии поля в пространстве вокруг прямолинейной нити постоянного тока – это концентрические окружности. Как найти напряженность магнитного поля на расстоянии от оси тока. Поскольку процесс неизменен во времени, первое уравнение Максвелла принимает вид: 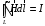 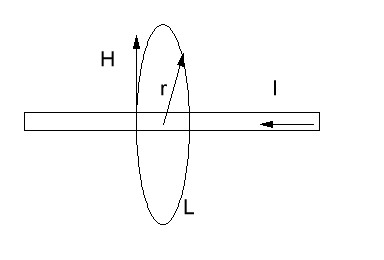 Рис. 4.1. Выберем силовую линию, радиус которой есть  и совместим с ней контур интегрирования и совместим с ней контур интегрирования 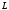 , а обходить будем его по направлению вектора , а обходить будем его по направлению вектора 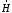 . Тогда под интегралом будет . Тогда под интегралом будет 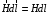 , причем , причем 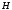 имеет одно и то же значение во всех точках контура, т.к. все радиальные направления равноправны. Поэтому: имеет одно и то же значение во всех точках контура, т.к. все радиальные направления равноправны. Поэтому: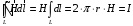 . .Таким образом, сразу получаем абсолютное значение напряженности магнитного поля как функции расстояния от оси тока. Остается выяснить взаимную ориентацию тока и поля. Поскольку согласно первому уравнению Максвелла при положительной циркуляции вектора 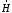 положителен и ток положителен и ток  , то при обходе контура вдоль , то при обходе контура вдоль 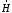 ток оказывается направленным по нормали к плоскости контура, связанной с направлением обхода правовинтовой системой. ток оказывается направленным по нормали к плоскости контура, связанной с направлением обхода правовинтовой системой.Третье и четвертое уравнения Максвелла 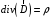 - третье уравнение - третье уравнение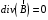 - четвертое уравнение - четвертое уравнениеСогласно третьему уравнению Максвелла расхождение электрической индукции равно плотности заряда. По смыслу понятия расхождения это означает, что электрические силовые линии могут начинаться или заканчиваться только в точках пространства, где 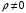 . Если же во всех точках некоей области . Если же во всех точках некоей области 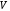 оказывается, что оказывается, что 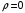 , то силовые линии либо пронизывают ее насквозь, либо являются замкнутыми. Поскольку при , то силовые линии либо пронизывают ее насквозь, либо являются замкнутыми. Поскольку при 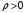 расхождение расхождение 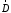 положительно, а при положительно, а при 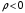 отрицательно, то «источниками» служат положительные заряды, а стоками – отрицательные. отрицательно, то «источниками» служат положительные заряды, а стоками – отрицательные.Проинтегрируем левую и правую части третьего уравнения Максвелла по объему 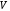 : :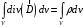 Интеграл справа выражает полный заряд, заключенный внутри объема: 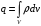 . .Слева применим теорему Остроградского-Гаусса, т.е. заменим объемный интеграл расхождения 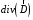 потоком потоком 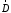 через замкнутую поверхность через замкнутую поверхность 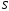 , являющуюся границей объема. В результате получаем интегральную формулировку закона электромагнетизма: , являющуюся границей объема. В результате получаем интегральную формулировку закона электромагнетизма: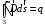 Это так называемая теорема Гаусса, согласно которой поток электрической индукции через любую замкнутую поверхность равен находящемуся внутри нее полному заряду. При этом не имеет значения как распределен заряд (возможно внутри объема имеется несколько заряженных областей). Если полный заряд внутри объема равен нулю, то поток вектора 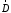 через через 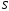 равен нулю: число силовых линий, входящих в объем равно числу выходящих. В частности, входящих и выходящих линий может вообще не быть. равен нулю: число силовых линий, входящих в объем равно числу выходящих. В частности, входящих и выходящих линий может вообще не быть. Рис. 4.2. Рассмотрим четвертое уравнение Максвелла. Равенство нулю расхождения магнитной индукции 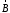 означает, что магнитные силовые линии – линии вектора означает, что магнитные силовые линии – линии вектора 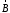 - нигде не начинаются и не кончаются: они или замкнуты или уходят в бесконечность. Интегральная форма, соответствующая четвертому уравнению Максвелла получается так же, как и для третьего: - нигде не начинаются и не кончаются: они или замкнуты или уходят в бесконечность. Интегральная форма, соответствующая четвертому уравнению Максвелла получается так же, как и для третьего: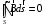 Поток магнитной индукции через любую замкнутую поверхность 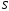 всегда равен нулю. всегда равен нулю.Непрерывность магнитных силовых линий соответствую отсутствию в природе магнитных зарядов. Строение электромагнитного поля Познакомившись со свойствами электромагнитного поля, которые выражают третье и четвертое уравнения Максвелла мы можем расширить круг представлений, связанный с первым и вторым уравнениями Максвелла. Рассмотрим взаимосвязи всех четырех уравнений. Сделаем некоторые заключения о строении электромагнитных полей. Возвратимся к примеру с прямолинейным проводником с постоянным током. Поскольку магнитное поле может в равной степени возбуждаться как током проводимости, так и током смещения, то очевидно, что магнитные силовые линии в виде концентрических окружностей свойственны не только осевому току проводимости, но и вообще любому осесимметричному распределению полного тока. Если имеется такой сгусток полного тока (а в частности, только тока проводимости или только тока смещения), то его окружает магнитное поле, описываемое концентрическими силовыми линиями. Причем полный ток и поле образуют правовинтовую систему. Предположим, что ток проводимости равен нулю. Тогда при наличии осевой симметрии мы должны обнаружить поле следующего вида: направления векторов 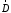 (или (или 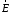 ) и ) и 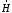 (или (или 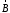 ) связаны правовинтовой системой, если ) связаны правовинтовой системой, если 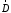 возрастает и левовинтовой системой, если возрастает и левовинтовой системой, если 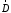 убывает. В первом случае векторы убывает. В первом случае векторы 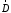 и и 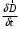 сонаправлены, во втором – направлены противоположны. сонаправлены, во втором – направлены противоположны.Пусть в некоторой области вектор 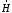 имеет неизменное направление. Введем декартову систему координат так, чтобы направление вектора имеет неизменное направление. Введем декартову систему координат так, чтобы направление вектора 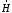 совпадало с осью z. Тогда совпадало с осью z. Тогда 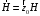 . . 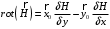 Следовательно, вектора 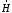 и и 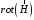 перпендикулярны, а потому взаимно перпендикулярны векторы напряженности магнитного поля перпендикулярны, а потому взаимно перпендикулярны векторы напряженности магнитного поля 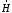 и и 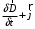 . . |
