Лекция 1 Аннотация
 Скачать 44.46 Kb. Скачать 44.46 Kb.
|
|
ЛЕКЦИЯ 1 Аннотация: Случайные, достоверные и невозможные события. Виды случайных событий: совместные и несовместные, противоположные события. Алгебра событий: сумма, произведение событий. Элементарные события (исходы). Классическое определение вероятности. Свойства вероятности случайного события. Прежде чем мы начнём первую лекцию, ответьте, пожалуйста, на вопрос. Предположим, вы попали в казино и планируете поставить фишку на рулетку. При вас пять раз подряд выпало красное. На какой цвет вы поставите? Многие решат, что ставить надо на чёрное, однако, и в этот раз нет никакой разницы, на какой цвет ставить, вероятности событий «пять раз подряд выпадало красное и шестой раз выпадет чёрное» и «шесть раз подряд выпадет красное» абсолютно одинаковы. И доказать это можно с помощью теории вероятностей. Часто при научном исследовании различных задач ученые сталкиваются с явлениями, которые при воспроизведении одного и того же опыта протекают каждый раз по-разному. Такие явления называются случайными, а науку, занимающуюся закономерностями в случайных явлениях, называют теорией вероятностей. В качестве первого термина теории вероятностей выделим понятие события. Событие – это любой результат испытания (опыта), который в этом испытаний может произойти или не произойти. События подразделяются по нескольким классификационным признакам. Рассмотрим некоторые из них. События называются несовместными, если появление одного из них исключает появление других в этом же испытании. И наоборот, если события могут произойти в одном испытаний, они называются совместными. Особо выделяют попарно несовместные события. Несколько событий образуют полную группу событий, если в результате испытания обязательно произойдёт хотя бы одно из них. Такие события могут быть как совместными, так и несовместными. Пример. Два стрелка стреляют по мишени. События «хотя бы один из них попал» и «хотя бы один из них не попал» образуют полную группу, в данном случае совместных событий. Если же события, образующие полную группу, попарно несовместны, то в результате испытания может произойти одно и только одно из них. Пример. Два стрелка стреляют по мишени. События «оба попали», «оба промахнулись», «только один попал» образуют полную группу попарно несовместных событий. События называются равновозможными (равновероятными), если нет оснований предполагать, что появление одного из них в испытании более возможно, чем появление других. События называются элементарными, если они образуют полную группу попарно несовместных, равновозможных событий. Событие называется достоверным, если в результате испытания оно обязательно происходит. Событие называется невозможным, если в результате испытания никогда не происходит. События, которые в испытании могут произойти или не произойти, называются случайными. Принято обозначать события заглавными буквами латинского алфавита. Часто достоверные события обозначают буквой 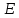 , а невозможным буквой , а невозможным буквой 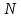 . . Событие называется благоприятствующим событию  , если появление этого события влечёт за собой появление события , если появление этого события влечёт за собой появление события  . . Классическое определение вероятности. Пожалуй, первое определение вероятности события даёт Якоб Бернулли в трактате «Искусство предположений» (1713): «Вероятность есть степень достоверности и отличается от неё, как часть от целого.» Далее ученый поясняет свою мысль на примере, из которого следует, что его понимание вероятности фактически совпадает с современным. Пусть некоторые события равновозможны и образуют полную группу попарно несовместных событий (элементарные события). Такую ситуацию называют классической, как и вероятность, вычисленную, исходя из этого предположения. Вероятностью случайного события  называется отношение числа благоприятствующих этому событию элементарных исходов к общему числу элементарных исходов. называется отношение числа благоприятствующих этому событию элементарных исходов к общему числу элементарных исходов. Иначе это можно выразить в виде формулы: 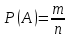 , ,где 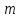 – число исходов, благоприятствующих – число исходов, благоприятствующих  ; ;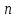 – общее число исходов испытания. – общее число исходов испытания. Пример. В урне 100 пронумерованных от 1 до 100 шаров. Наудачу вынимается шар. Какова вероятность, что его номер содержит ноль. Число благоприятствующих событий равно числу шаров, содержащих в своём номере ноль, таких шаров 9. Общее число шаров 100. Таким образом  Из определения вероятности вытекают её свойства: Вероятность достоверного события равна единице. Вероятность невозможного события равна нулю. Вероятность случайного события есть положительное число, заключенное между нулём и единицей. При непосредственном подсчете вероятностей часто используют формулы комбинаторики. Перечислим основные из них. Перестановками называют комбинации, состоящие из одних и тех же элементов и отличающиеся только порядком их расположения. Общее число перестановок вычисляется по формуле:  Размещениями называют комбинации, составленные из 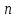 различных элементов по различных элементов по 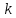 элементов, отличающиеся или составом элементов, или порядком их расположения. Число всех возможных размещений вычисляется по формуле: элементов, отличающиеся или составом элементов, или порядком их расположения. Число всех возможных размещений вычисляется по формуле: Сочетаниями называют комбинации, составленные из 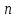 различных элементов по различных элементов по 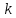 элементов, отличающиеся хотя бы одним элементом. Общее число сочетаний вычисляется по формуле: элементов, отличающиеся хотя бы одним элементом. Общее число сочетаний вычисляется по формуле: 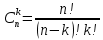 Данные выше формулы относятся к случаям, когда все элементы различны. Рассмотрим также случаи, когда элементы могут повторяться. Пусть имеются 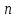 объектов объектов 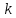 типов: первого типа типов: первого типа  штук, второго типа штук, второго типа  штук и так далее. Тогда общее число перестановок с повторениями вычисляется по формуле: штук и так далее. Тогда общее число перестановок с повторениями вычисляется по формуле: Пусть имеются предметы 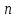 различных типов. Количество различных комбинаций, состоящих из различных типов. Количество различных комбинаций, состоящих из 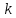 элементов и отличающихся или составом, или порядком расположения элементов называют размещениями с повторениями. Общее число размещений с повторениями вычисляется по формуле: элементов и отличающихся или составом, или порядком расположения элементов называют размещениями с повторениями. Общее число размещений с повторениями вычисляется по формуле: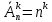 Пусть имеются предметы 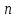 различных типов, количество различных комбинаций, состоящих из различных типов, количество различных комбинаций, состоящих из 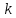 элементов и отличающихся хотя бы одним элементом называют сочетаниями с повторениями. Общее число сочетаний с повторениями вычисляется по формуле: элементов и отличающихся хотя бы одним элементом называют сочетаниями с повторениями. Общее число сочетаний с повторениями вычисляется по формуле: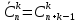 Правило суммы. Если объект  может быть выбран из некоторой совокупности объектов может быть выбран из некоторой совокупности объектов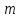 способами, а другой объект способами, а другой объект 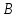 – – 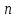 способами, то выбрать либо А, либо В можно способами, то выбрать либо А, либо В можно 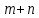 способами. способами.Правило произведения. Если объект  может быть выбран из некоторой совокупности объектов может быть выбран из некоторой совокупности объектов 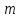 способами и после каждого такого выбора объект способами и после каждого такого выбора объект 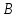 может быть выбран может быть выбран 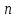 способами, то пара объектов способами, то пара объектов 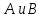 в указанном порядке может быть выбрана в указанном порядке может быть выбрана  способами. способами.Рассмотрим здесь одну из важных задач теории вероятностей. Пример. В урне 15 шаров: 5 белых и 10 чёрных. Наудачу вынимают 7 шаров. Какова вероятность, что среди них 2 белых и 5 чёрных? Решение. Общее число исходов этого испытания равно числу способов, которыми можно извлечь 7 шаров из 15, то есть  . Рассчитаем количество благоприятствующих . Рассчитаем количество благоприятствующих 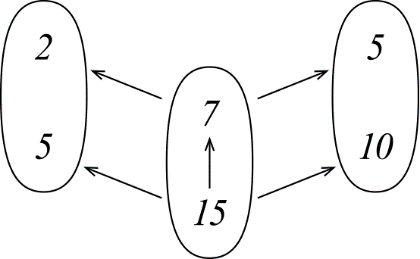 исходов. Количество комбинаций, позволяющих вынуть 2 белых шара из 5: исходов. Количество комбинаций, позволяющих вынуть 2 белых шара из 5: 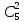 , очевидно, что остальные 5 шаров должны быть чёрными и количество комбинаций , очевидно, что остальные 5 шаров должны быть чёрными и количество комбинаций  . .Тогда вероятность интересующего нас события:  Эту задачу можно обобщить. Пусть 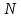 – общее количество объектов, из которых – общее количество объектов, из которых 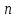 штук о штук о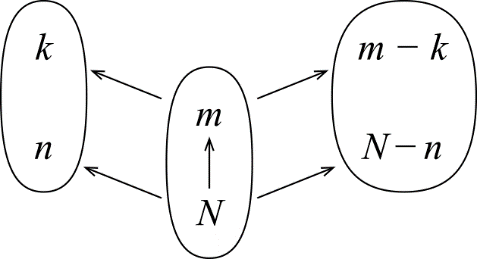 дного сорта и дного сорта и  штук другого сорта. Производится выбор штук другого сорта. Производится выбор 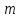 объектов. Причём, объектов. Причём, 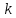 выбранных объектов должны быть первого сорта, а остальные – другого сорта. Тогда выбранных объектов должны быть первого сорта, а остальные – другого сорта. Тогда 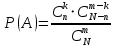 Классическое определение вероятности имеет ряд недостатков: Требование конечности числа исходов испытания. Невозможность во многих случаях представить результат испытания в виде совокупности исходов. Невозможность зачастую считать такие исходы равновозможными. К примеру, при стрельбе по мишени существуют два исхода: попадание и промах. Если считать вероятность попадания по классической формуле, то в результате получается 0,5, что, очевидно, чаще всего не соответствует действительности. Таким образом применение классической формулы для подсчёта вероятностей возможно лишь в некоторых случаях. В настоящее понятие вероятности связывают с эмпирическим понятием частоты. Относительной частотой события  называют отношение количества испытаний, в которых это событие появилось называют отношение количества испытаний, в которых это событие появилось  к общему количеству испытаний к общему количеству испытаний  : :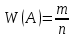 Легко можно доказать, что относительная частота, как и вероятность, принимает положительные значения, заключенные между нулём и единицей включительно. Длительные наблюдения показали, что относительная частота обнаруживает свойство устойчивости, заключающееся в том, что при большом количестве опытов, производимых в одинаковых условиях, относительная частота в различных сериях опытов изменяется мало и колеблется около некоторого числа, которое является вероятностью события  . . Относительную частоту или число к ней близкое принимают за статистическую вероятность. Для существования статистической вероятности необходимо: Возможность, хотя бы принципиально, производить неограниченное количество испытаний. Устойчивость относительных частот в различных сериях. Недостатком статистического определения очевидно является неоднозначность статистической вероятности и трудности, связанные с проведением опытов. Алгебра событий. Суммой (или объединением) событий  и и 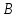 называется событие, обозначаемое называется событие, обозначаемое  , которое состоит в наступлении хотя бы одного из событий , которое состоит в наступлении хотя бы одного из событий  или или 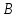 , то есть или события , то есть или события  , или события , или события 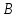 , или обоих этих событий. , или обоих этих событий. Очевидно, что если события  и и 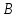 несовместны, то сумма этих событий состоит в наступлении одного и только одного из этих событий. несовместны, то сумма этих событий состоит в наступлении одного и только одного из этих событий. Произведением (или совмещением) событий  и и 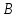 называется событие, обозначаемое называется событие, обозначаемое  , которое состоит в одновременном наступлении событий , которое состоит в одновременном наступлении событий  и и 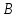 . . |
