Элетрическоеполе. 1. Электрическое поле. Лекция 1. Электрическое поле Цель ознакомиться с понятием электрического поля, его характеристиками и законами
 Скачать 198 Kb. Скачать 198 Kb.
|
|
Лекция №1. Электрическое поле Цель: ознакомиться с понятием электрического поля, его характеристиками и законами Определение и изображение электрического поля Электрические свойства тел объясняются присутствием в них заряженных частиц. Такие частицы, как электрон и протон, имеют равные по абсолютному значению заряды, при этом заряд электрона отрицателен, а заряд протона положителен. Указанные частицы вместе с нейтронами входят о состав атомов вещества, однако они могут находиться и в свободном состоянии. Если тело заряжено, то в нем преобладают положительные или отрицательные заряды; если число тех и других зарядов одинаково, то тело в электрическом отношении нейтрально. Тела с одноименными зарядами отталкиваются, тела с разноименными зарядами притягиваются. Электрически заряженное тело неразрывно связано с окружающим его электрическим полем, через которое и осуществляется взаимодействие электрически заряженных тел. Электрическое поле – одна из двух сторон электромагнитного поля, характеризующаяся воздействием на электрически заряженную частицу с силой, пропорциональной заряду частицы и не зависящей от ее скорости. Электрическое поле является силовым или векторным. Для обнаружения и изучения электрического поля используются пробные неподвижные точечные заряженные тела с очень малым положительным зарядом q. Линейные размеры точечных заряженных тел очень малы по сравнению с расстоянием до точек, в которых рассматривается их электрическое поле. Мы будем рассматривать электростатические поля, т. е. такие, которые создаются неподвижными заряженными телами, для краткости называя их просто электрическими полями. Р 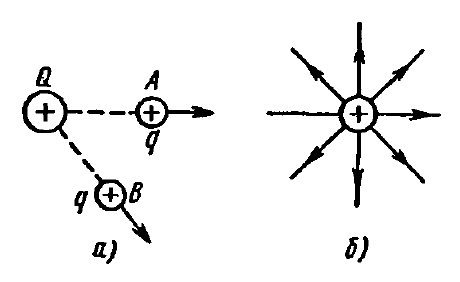 ассмотрим электрическое поле уединенного неподвижного точечного заряженного тела с зарядом Q(см. рис. а), расположенного в произвольной точке горизонтальной плоскости. Поместим в точку А этой плоскости пробное заряженное тело с зарядом q. Поскольку сила отталкивания, действующая на пробное заряженное тело, лежит на линии, соединяющей центры взаимодействующих заряженных тел, пробное заряженное тело будет перемещаться в радиальном направлении (так же, как и пробное заряженное тело, помещенное в точку В). Помещая пробное заряженное тело в другие точки и продолжая эти рассуждения. получим картину, которая условно изображает электрическое папе с помощью линий, называемых силовыми (рис. б). В частном случае уединенного точечного заряженного тела силовые линии представляют собой прямые, проведенные через точку, в которой находится это тело. В общем случае вектор силы, с которой поле действует на пробное заряженное тело в данной точке поля, совпадает с касательной к силовой линии в этой точке. ассмотрим электрическое поле уединенного неподвижного точечного заряженного тела с зарядом Q(см. рис. а), расположенного в произвольной точке горизонтальной плоскости. Поместим в точку А этой плоскости пробное заряженное тело с зарядом q. Поскольку сила отталкивания, действующая на пробное заряженное тело, лежит на линии, соединяющей центры взаимодействующих заряженных тел, пробное заряженное тело будет перемещаться в радиальном направлении (так же, как и пробное заряженное тело, помещенное в точку В). Помещая пробное заряженное тело в другие точки и продолжая эти рассуждения. получим картину, которая условно изображает электрическое папе с помощью линий, называемых силовыми (рис. б). В частном случае уединенного точечного заряженного тела силовые линии представляют собой прямые, проведенные через точку, в которой находится это тело. В общем случае вектор силы, с которой поле действует на пробное заряженное тело в данной точке поля, совпадает с касательной к силовой линии в этой точке. Закон Кулона. Напряженность электрического поля Взаимодействие точечных заряженных тел описывается законом Кулона. С 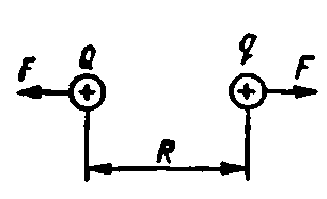 ила взаимодействия F между точечными заряженными телами Q и q, расположенными в данной среде на расстоянии R друг от друга (см. рис.), прямо пропорциональна произведению зарядов этих тел и обратно пропорциональна квадрату расстояния между ними: ила взаимодействия F между точечными заряженными телами Q и q, расположенными в данной среде на расстоянии R друг от друга (см. рис.), прямо пропорциональна произведению зарядов этих тел и обратно пропорциональна квадрату расстояния между ними: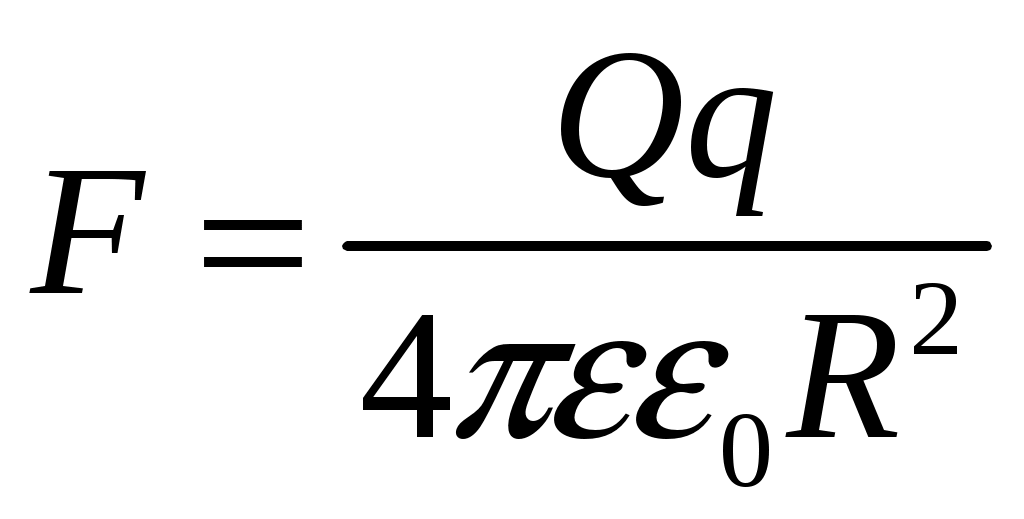 , , где Q и q – значения зарядов, Кл (1 Кл = 6,31018 зарядов электрона); – относительная диэлектрическая проницаемость среды, показывающая, во сколько раз сила взаимодействия в данной среде меньше, чем в вакууме (величина безразмерная); 0 = 8,8610–12 Ф/м – электрическая постоянная. Введем силовую характеристику поля – напряженность: 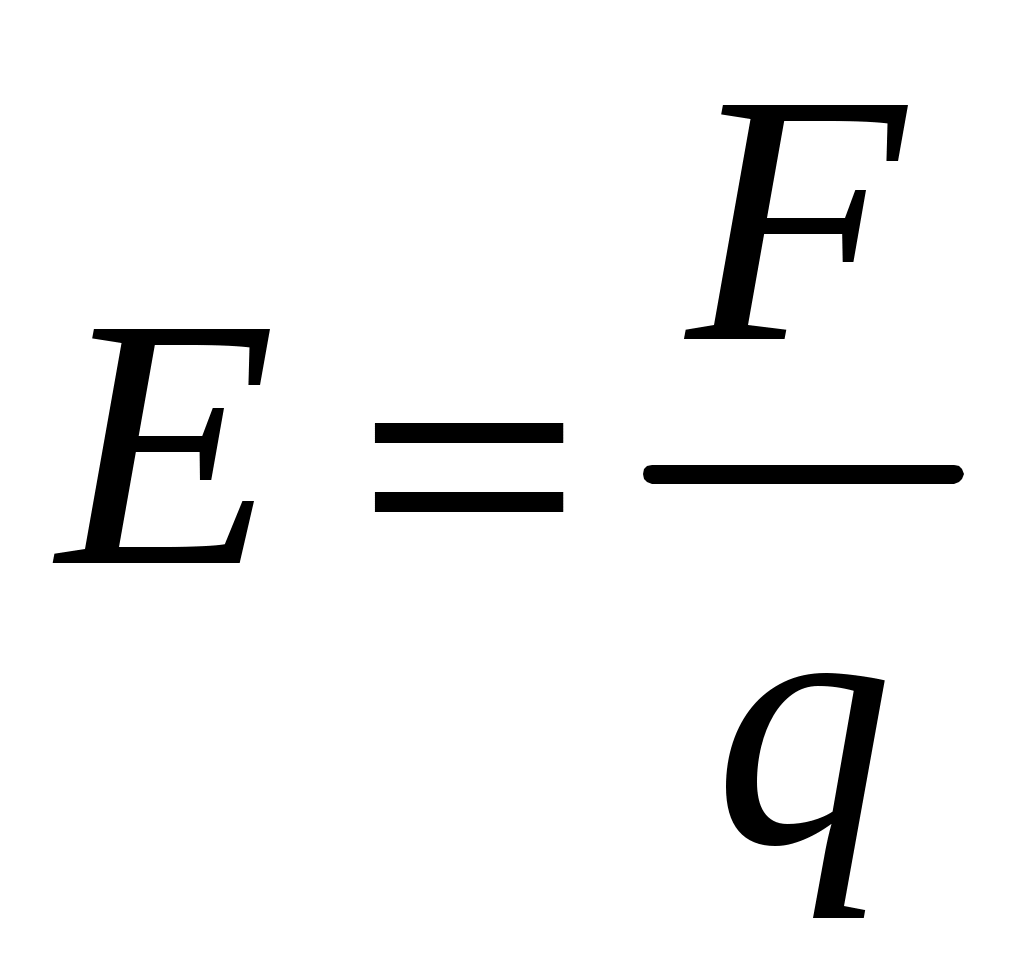 Напряженность электрического поля в данной точке определяется силой, действующей на помещенное в эту точку пробное тело, обладающее единичным положительным зарядом. Единица напряженности [E] = Н/Кл (ньютон на кулон). Для поля уединенного точечного заряженного тела на основании закона Кулона 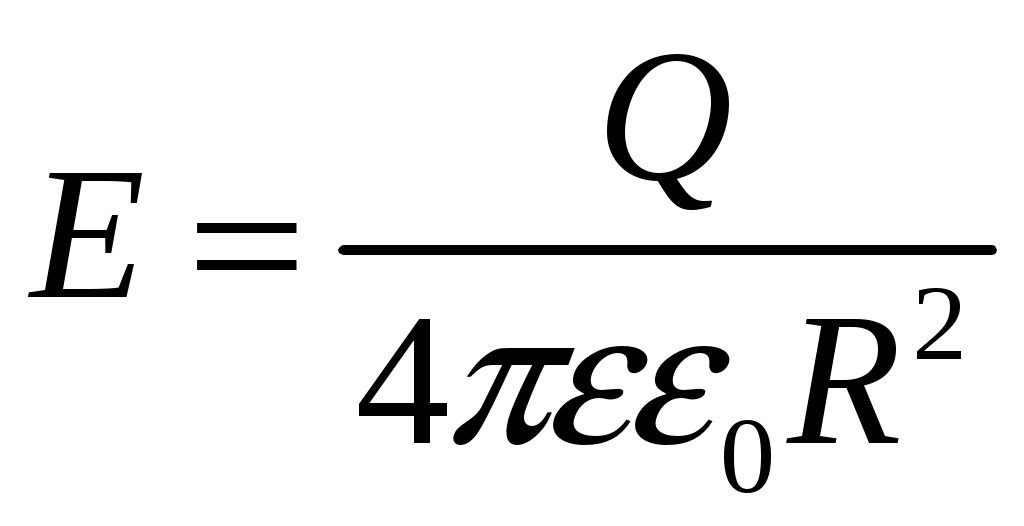 . .Потенциал. Электрическое напряжение Пусть уединенное неподвижное точечное заряженное тело е зарядом Q расположено в произвольной точке горизонтальной плоскости (см. рис.). Если в точке А окажется пробное заряженное тело с зарядом q, то под действием силы FA оно станет перемешаться. При этом за счет энергии поля заряда Q будет с 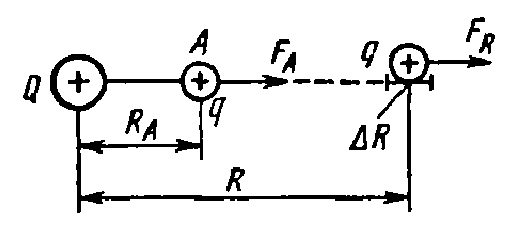 овершаться определенная работа. Поскольку сила овершаться определенная работа. Поскольку сила 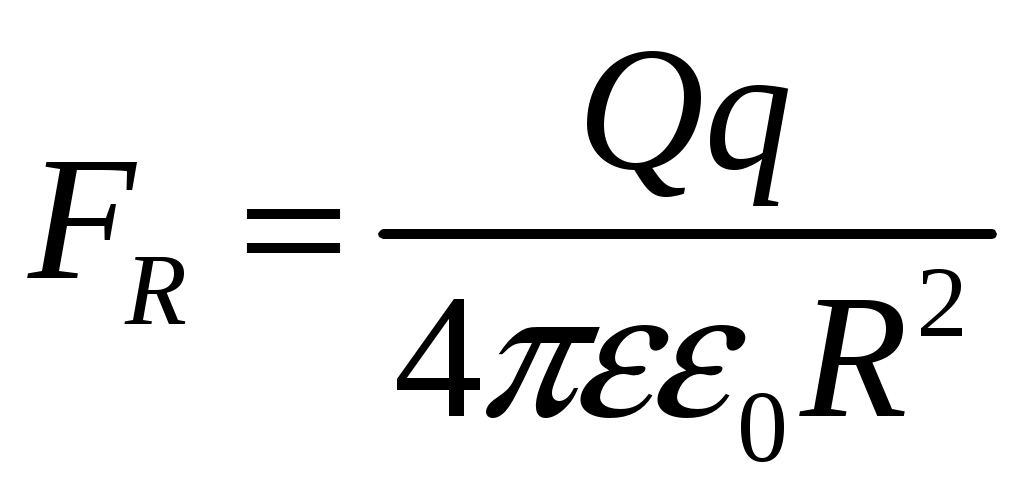 непрерывно меняется, для нахождения работы, которую совершает поле, перемещая пробное заряженное тело из данной точки в бесконечность, разобьем весь путь на элементарные участки R,так что в пределах каждого такого участка силу FRможно считать неизменной. непрерывно меняется, для нахождения работы, которую совершает поле, перемещая пробное заряженное тело из данной точки в бесконечность, разобьем весь путь на элементарные участки R,так что в пределах каждого такого участка силу FRможно считать неизменной.Тогда элементарная работа этой силы Для определения всей работы А необходимо просуммировать элементарные работы A на участке пути от Ra до бесконечности. Тогда 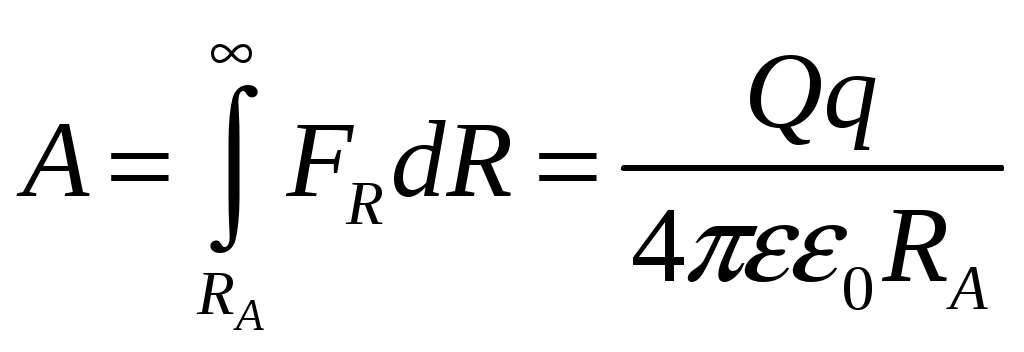 . .Индекс A обычно опускают и записывают 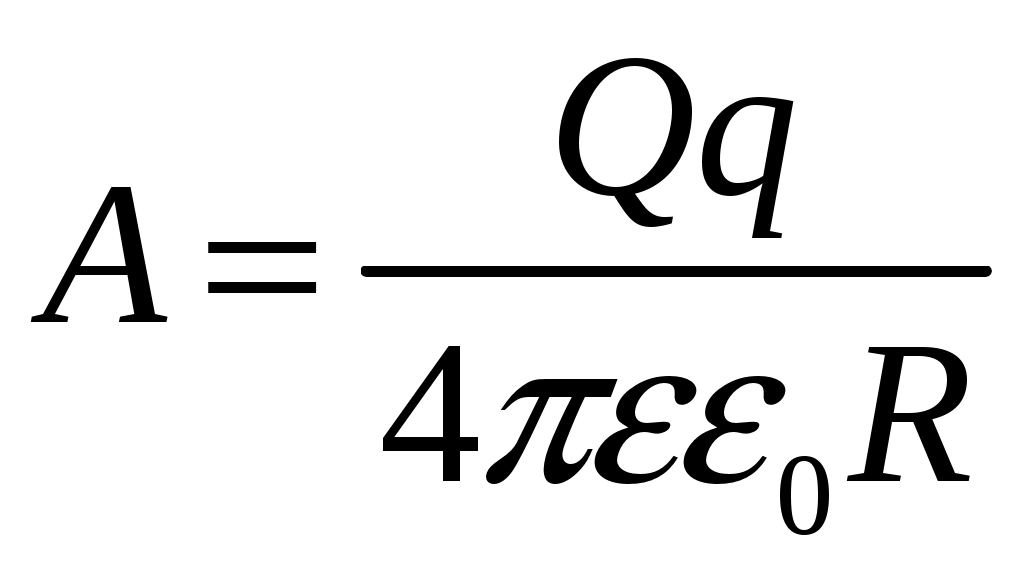 . .Работа выражается в джоулях (Дж). Введем энергетическую характеристику поля – потенциал . Потенциалом электрического поля заряда Qв данной точке называют величину, численно равную работе, которую совершает поле, перемещая пробное тело, обладающее единичным положительным зарядом, из данной точки в бесконечность: 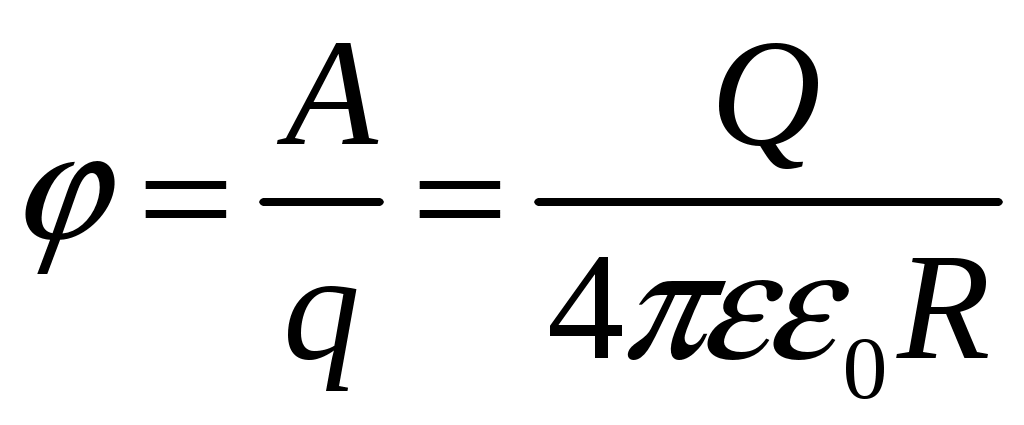 . .Единица потенциала [] = 1 Дж / 1 Кл = 1 В. Потенциал данной точки поля равен 1 В, если при переносе пробного тела с зарядом в 1 Кл из данной точки в бесконечность совершается работа в 1 Дж. В том случае, когда заряженное тело, создающее папе, имеет отрицательный заряд, поле будет препятствовать удалению пробного заряженного тела, т. е. потенциал поля будет отрицательным. Определив потенциал электрического заряда Qв точках А и В, найдем их разность, которую называют электрическим напряжением между двумя точками поля: Таким образом, электрическим напряжением или разностью потенциалов между двумя точками поля называют величину, численно равную работе, которую совершает поле, перемещая между этими точками пробное тело, обладающее единичным положительным зарядом. Понятие электрической емкости Если изолированному проводнику сообщить электрический заряд, то вокруг такого проводника образуется электрическое поле, а сам проводник приобретет потенциал. Чем больше величина заряда Q, тем выше потенциал проводника и тем большей потенциальной энергией обладает электрическое поле. Для данного проводника, находящегося в неизменной среде, отношение заряда к потенциалу есть величина постоянная. Эта величина называется электрической емкостью или просто емкостью данного проводника и обозначается буквой С и определяется по формуле: 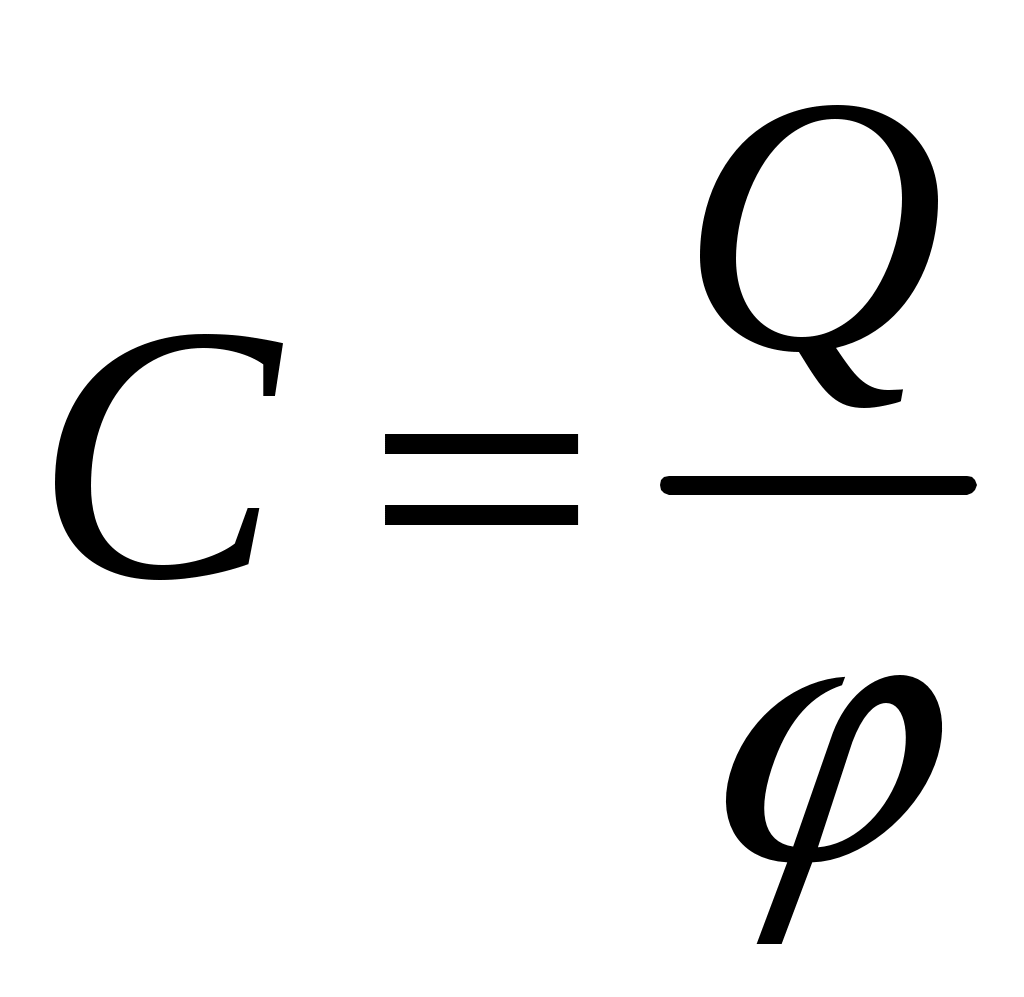 . .Единицей емкости служит фарад (Ф). Фарад – это емкость такого проводника, потенциал которого повышается на 1 В при сообщении проводнику заряда 1 Кл. Фарад – крупная единица, поэтому часто емкость выражают в микрофарадах (1 мкФ= 10–6 Ф) и пикофарадах (1 пФ = 10–12 Ф). Емкость проводника не зависит от массы проводника и от того, из какого материала он сделан. Но емкость проводника находится в прямой зависимости от диэлектрической проницаемости среды. Если, например, проводник перенести из воздуха в керосин, то его емкость увеличится примерно в 2 раза. Кроме того, емкость зависит от формы проводника и от того, есть ли по соседству с ним другие проводники и на каком расстоянии от него они находятся. Если расположить по соседству несколько проводников, то нужно рассматривать емкость системы этих проводников, а не емкость одного заряжаемого проводника. При сближении проводников емкость системы увеличивается. Обычно используется система из двух проводников. Достигнуть значительной величины емкости такой системы можно, если взять проводники большой поверхности и расположить их в среде с большой диэлектрической проницаемостью на незначительном расстоянии один от другого. Система проводников такого устройства называется конденсатором. Электрическая емкость конденсатора К 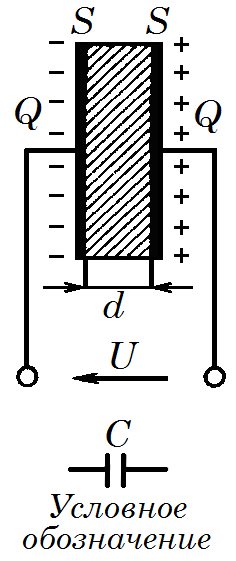 онденсатор представляет собой устройство, состоящее из двух металлических пластин или проводников произвольной формы (обкладок), разделенных диэлектриком. Простейший по устройству плоский конденсатор образуется плоскими параллельно расположенными металлическими пластинами, разделенными слоем изоляции (см. рис.). Если пластины конденсатора присоединить к источнику питания с постоянным напряжением U, то на них образуются равные по величине, но противоположные по знаку электрические заряды +Q и –Q. онденсатор представляет собой устройство, состоящее из двух металлических пластин или проводников произвольной формы (обкладок), разделенных диэлектриком. Простейший по устройству плоский конденсатор образуется плоскими параллельно расположенными металлическими пластинами, разделенными слоем изоляции (см. рис.). Если пластины конденсатора присоединить к источнику питания с постоянным напряжением U, то на них образуются равные по величине, но противоположные по знаку электрические заряды +Q и –Q.Явление накопления заряда в конденсаторе связано с возникновением электрического поля в его диэлектрике. Под действием сил поля на поверхностях диэлектрика, прилегающих к его обкладкам, возникают связанные заряды. Они отталкивают одноименные заряды обкладок и притягивают разноименные. В результате на одной обкладке конденсатора образуется положительный заряд, а на другой – отрицательный. Емкостью конденсатора называется величина, численно равная заряду, который нужно сообщить одной из обкладок, чтобы разность потенциалов (напряжение) между ними повысилась на единицу, т. е. 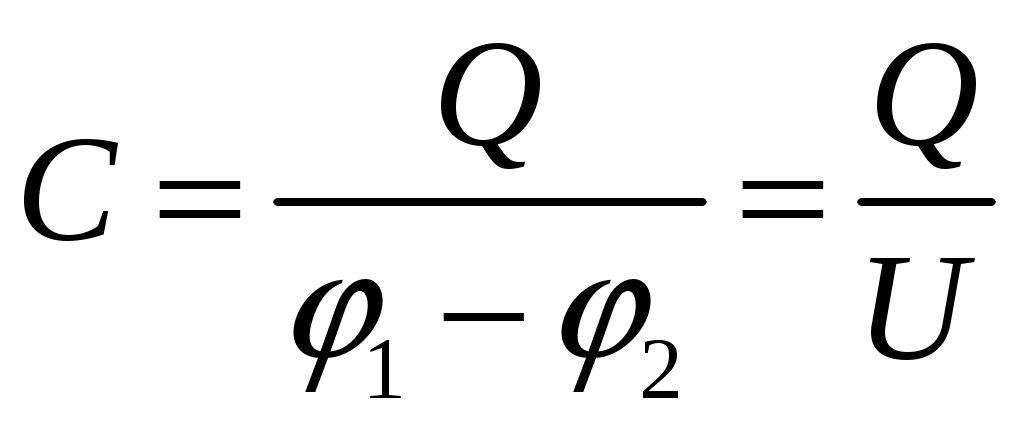 . .Емкостью в 1 Ф обладает конденсатор, у которого при заряде каждой обкладки в 1 Кл напряжение между ними равно 1 В. Конденсаторы различаются формой обкладок, типом диэлектрика (слюда, бумага, керамика) и емкостью. В электролитических конденсаторах диэлектриком служит тонкая пленка оксида алюминия с очень высокой диэлектрической проницаемостью. Такие конденсаторы имеют большую емкость при сравнительно небольших размерах и применяются только в цепях постоянного тока. Каждый конденсатор характеризуется номинальными емкостью и напряжением, которое длительное время выдерживает его диэлектрик. Воздушные конденсаторы состоят из системы подвижных пластин (ротора) и системы неподвижных пластин. При перемещении ротора изменяется активная площадь пластин, т. е. площадь, находящаяся в электрическом поле. Воздушные конденсаторы применяются в качестве плавно регулируемых небольших переменных емкостей. По форме обкладок конденсаторы подразделяются на плоские, цилиндрические и сферические. Емкость плоского конденсатора можно определить по формуле Из последней формулы видно, что емкостьплоского конденсаторапрямо пропорциональна диэлектрической проницаемости диэлектрика, площади пластин и обратно пропорциональна расстоянию между пластинами. Для цилиндрического конденсатора: 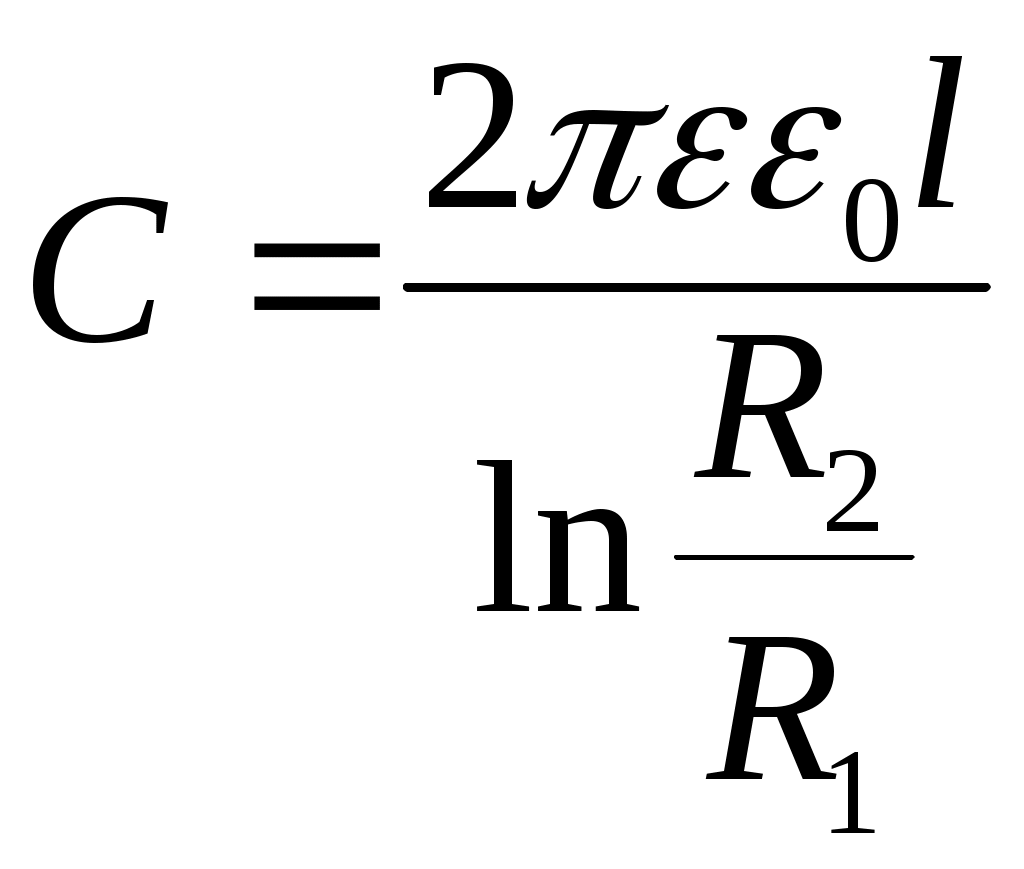 , ,где l – длина цилиндрических обкладок, R1 и R2 – радиусы внутренней и внешней обкладок конденсатора, соответственно. Если между обкладками конденсатора находится воздух, то полагаем =1. Для сферического конденсатора: где R1 и R2– радиусы внутренней и внешней обкладок конденсатора, соответственно. Если между обкладками конденсатора находится воздух, то полагаем =1. Последовательное соединение конденсаторов П 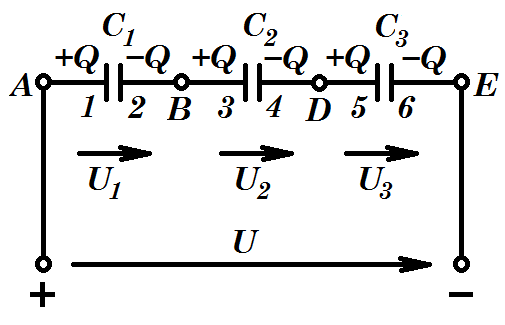 ри отсутствии конденсатора нужной емкости его можно заменить несколькими конденсаторами с другими параметрами. Когда емкость одного конденсатора мала, то соединяют несколько конденсаторов параллельно. Если напряжение велико и диэлектрик конденсатора может быть пробит, применяется последовательное соединение конденсаторов, иногда используется и смешанное соединение. ри отсутствии конденсатора нужной емкости его можно заменить несколькими конденсаторами с другими параметрами. Когда емкость одного конденсатора мала, то соединяют несколько конденсаторов параллельно. Если напряжение велико и диэлектрик конденсатора может быть пробит, применяется последовательное соединение конденсаторов, иногда используется и смешанное соединение.На рисунке конденсаторы С1 – С3 соединены последовательно. С источником энергии соединяются только крайние обкладки: обкладка 1 соединяется с положительным полюсом источника, а обкладка 6 с отрицательным. Эти обкладки получают электрические заряды +Q и –Q непосредственно от источника энергии. Обкладки 2–5 заряжаются вследствие электростатической индукции. На обкладках 2 и3, соединенных проводником B,и обкладках 4 и 5, соединенных проводником D, происходит разделение зарядов, нейтрализовавших друг друга. Таким образом, при последовательном соединении конденсаторов на всех обкладках возникают одинаковые электрические заряды. Напряжение источника энергии можно представить как разность потенциалов поля в точках А и E, т. е. Напряжения на конденсаторах равны: Левая часть полученного равенства выражает сумму напряжений конденсаторов, а правая – напряжение, которое подводится от источника энергии, т. е. Таким образом, при последовательном соединении конденсаторов сумма напряжений равна приложенному к цепи напряжению. Пользуясь формулой 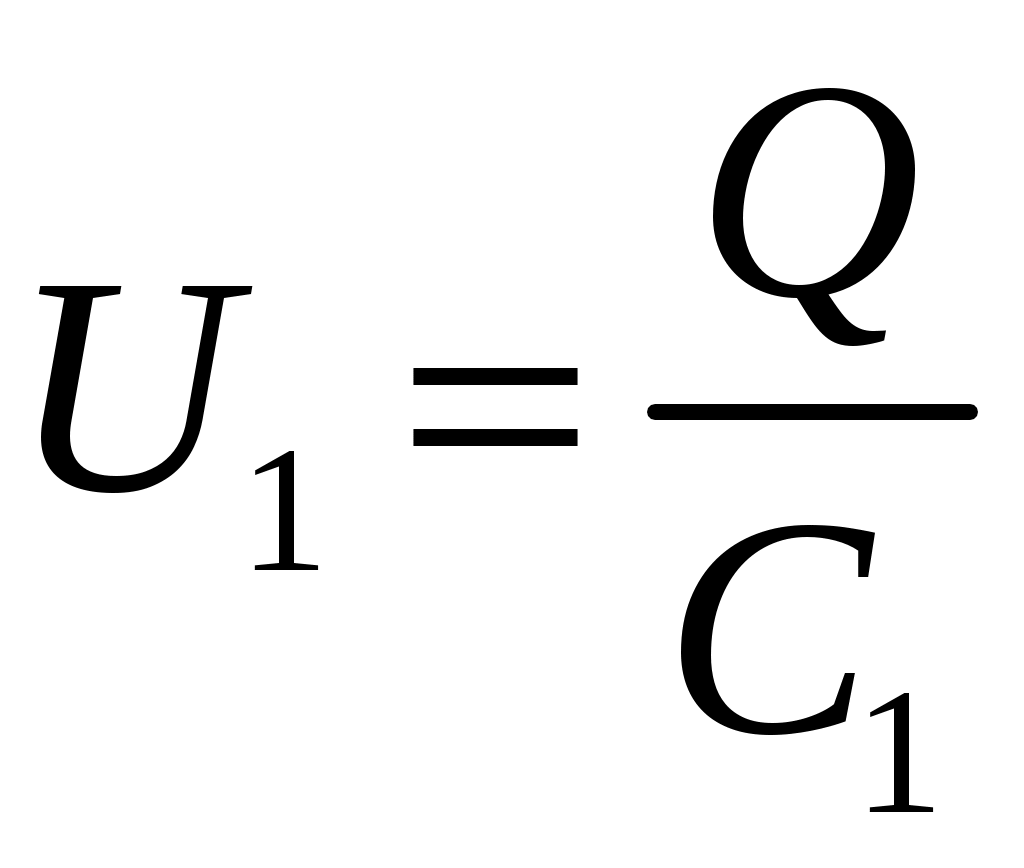 ; ; 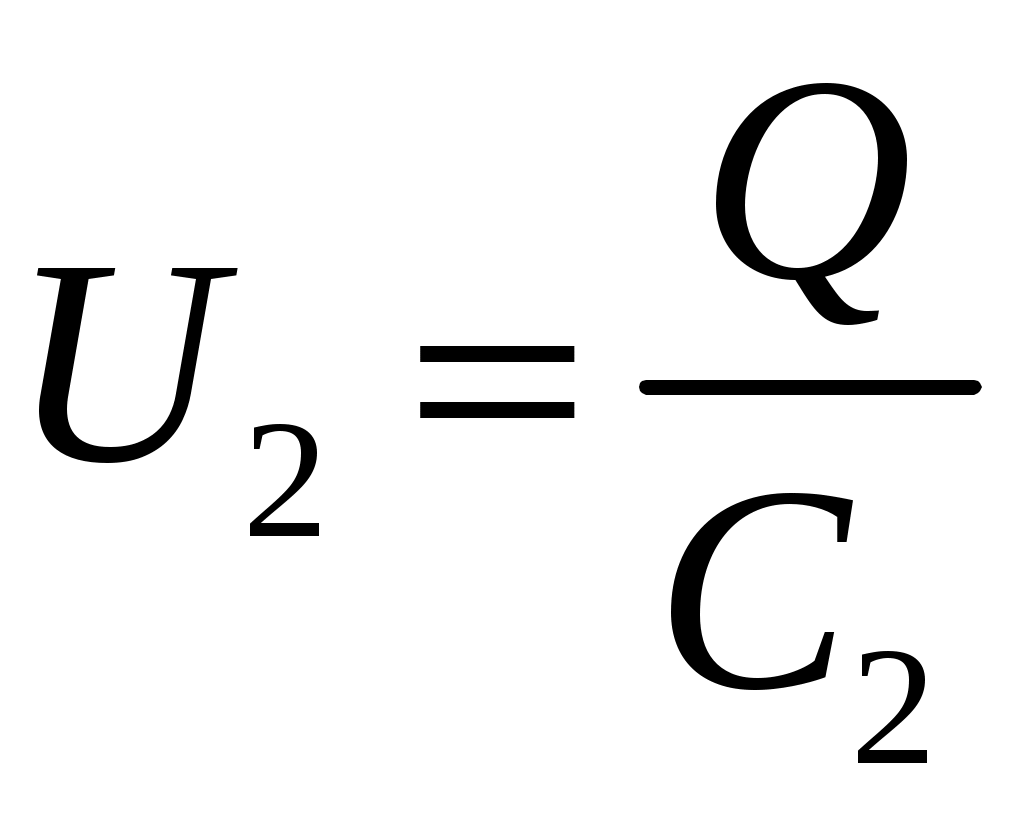 ; ; 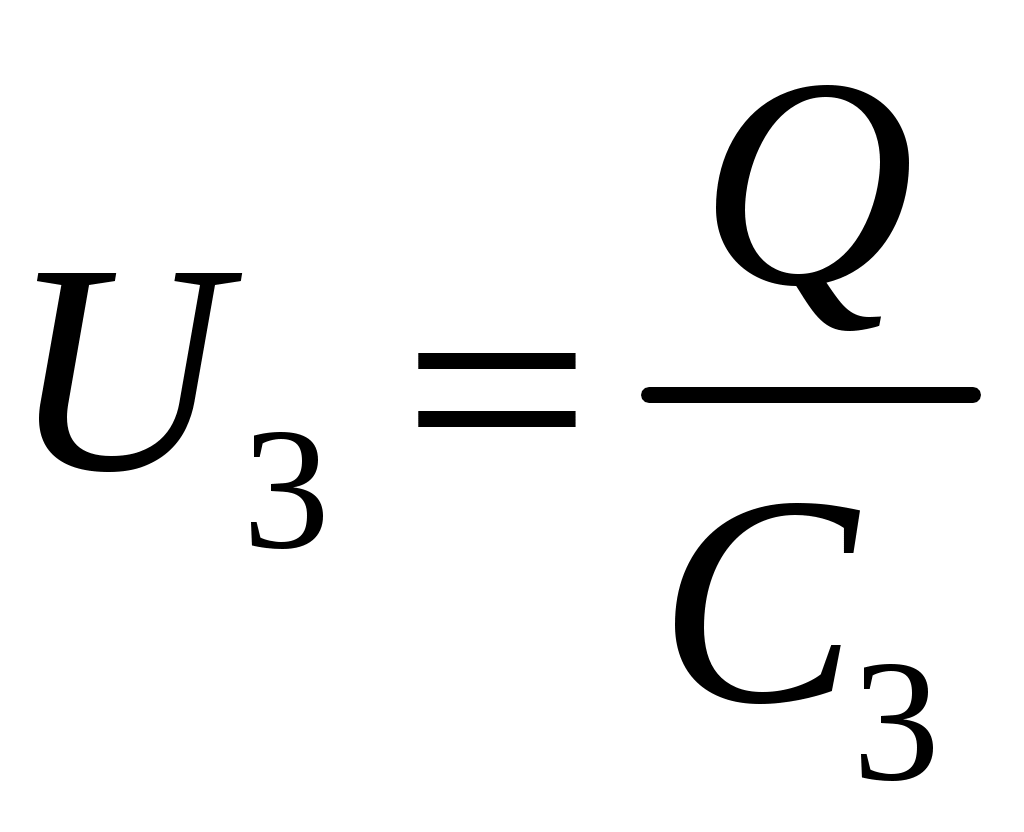 . .Из данных формул видно, что при различных значениях емкостей включенных последовательно конденсаторов напряжения на них будут различными: чем больше емкость конденсатора, тем меньше напряжение на нем. Цепь последовательно соединенных конденсаторов можно заменить одним эквивалентным конденсатором с емкостью С. Эквивалентность этого конденсатора состоит в том, что он под действием напряжения U приобретает такой же заряд Q, как и вся батарея последовательно соединенных конденсаторов. Общее напряжение выразим через эквивалентную емкость: Тогда 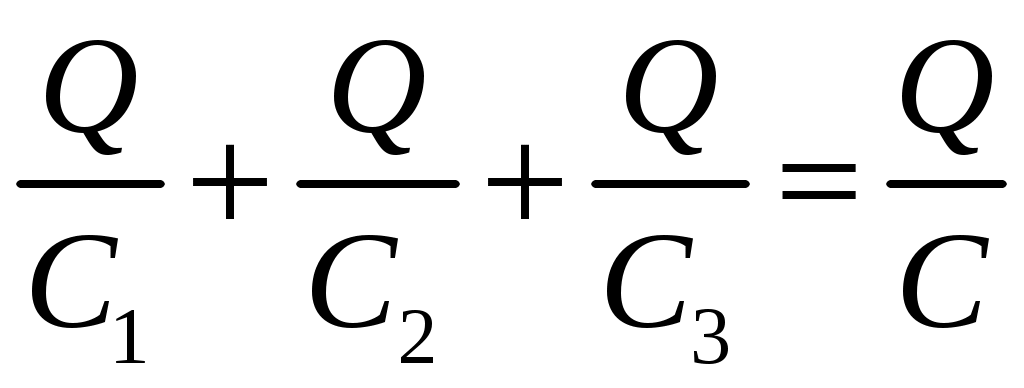 . Сократив на Q, получим . Сократив на Q, получим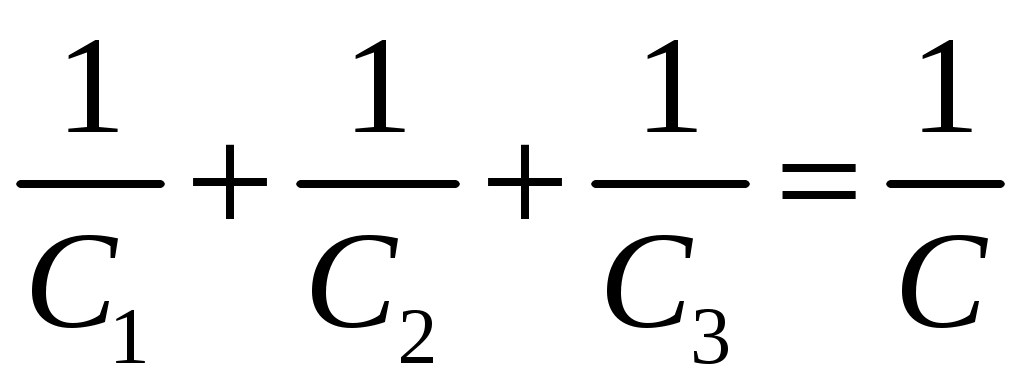 . .Таким образом, при последовательном соединении конденсаторов величина, обратная эквивалентной емкости, равна сумме обратных величин емкостей отдельных конденсаторов. Для последовательного соединения двух конденсаторов (емкостью С1 и С2) 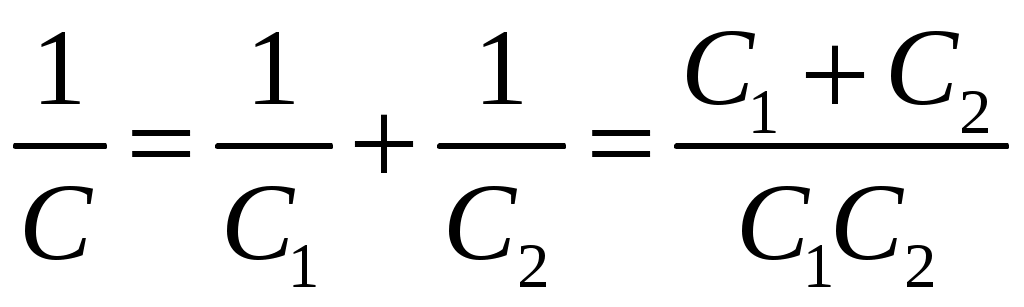 , или , или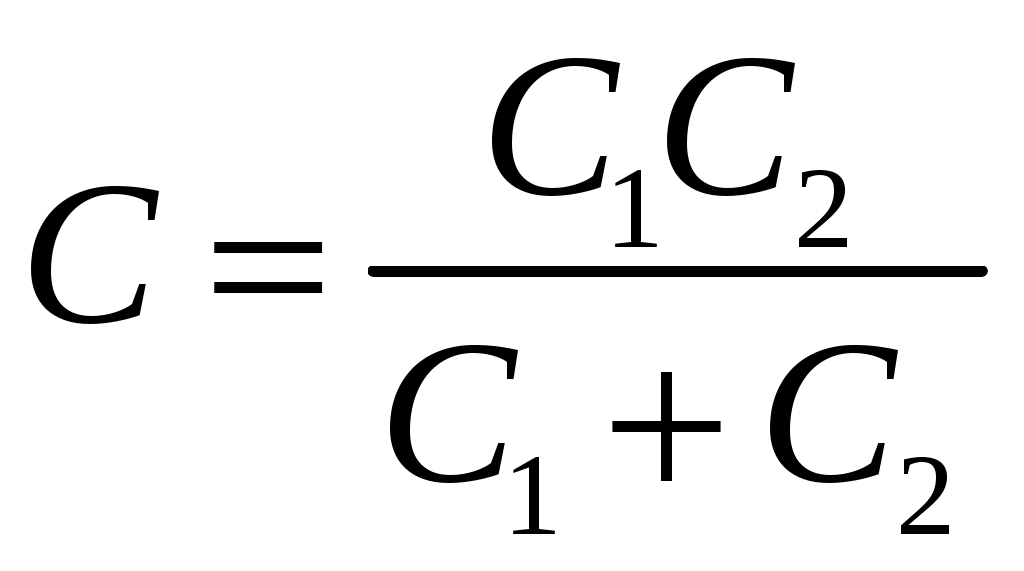 . .Если последовательно соединяют п одинаковых конденсаторов емкостью Сn, то эквивалентная емкость Эквивалентная емкость при последовательном соединении конденсаторов меньше емкости самого малого из них. Это можно объяснить тем, что между обкладками 1 и 6 (см. рис. выше), к которым присоединяется источник энергии, находятся диэлектрики всех трех конденсаторов. С увеличением толщины диэлектрика (расстояния между пластинами) емкость конденсатора снижается. С увеличением толщины диэлектрика увеличивается пробивное, а, следовательно, и допустимое рабочее напряжение. Поэтому последовательное соединение конденсаторов применяется для увеличения допустимого рабочего напряжения всей цепи конденсаторов. П 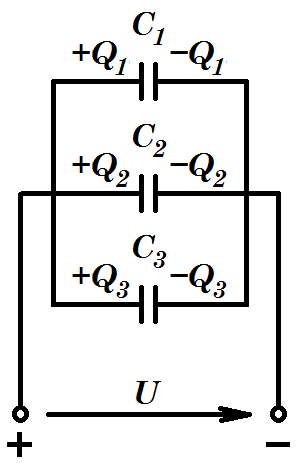 араллельное соединение конденсаторов араллельное соединение конденсаторовВыше было сказано, что при последовательном соединении конденсаторов их эквивалентная емкость уменьшается, а общее допустимое рабочее напряжение увеличивается. Так, цепь с последовательным соединением трех конденсаторов с одинаковой емкостью 3 мкФ и допустимым рабочим напряжением 200 В можно заменить одним конденсатором емкостью 1 мкФ и допустимым рабочим напряжением 600 В. На практике часто требуется увеличить не допустимое рабочее напряжение, а эквивалентную емкость, для чего конденсаторы соединяют параллельно (см. рис.). При этом их подключают к одним и тем же зажимам – полюсам источника энергии. Следовательно, они находятся под одним напряжением, т. е. Заряды на обкладках отдельных конденсаторов прямо пропорциональны их емкости: Общий заряд равен сумме зарядов на отдельных конденсаторах: Эквивалентная емкость трех параллельно соединенных конденсаторов Таким образом, при параллельном соединении конденсаторов эквивалентная емкость равна сумме емкостей отдельных конденсаторов. Это объясняется тем, что при параллельном соединении как бы увеличивается общая поверхность каждой из разноименно заряженных пластин. Кроме рассмотренных схем соединения конденсаторов, возможно, также, их смешанное соединение (последовательное и параллельное). Поэтому при расчете таких электростатических цепей пользуются формулами для последовательного и параллельного соединения конденсаторов. Вопросы для самоконтроля: 1. Что называется электрическим полем? 2. Сформулируйте и напишите закон Кулона. 3. Что называется напряженностью электрического поля? 4. Что представляет собой электрический потенциал и в чем измеряется? 5. Что называется электроемкостью уединенного проводника, от чего она зависит и в чем измеряется? 6. Что называется электроемкостью конденсатора и от чего она зависит? 7. От каких величин зависит емкость плоского конденсатора? 8. Чему равна электроемкость цилиндрического и сферического конденсатора? 9. Приведите формулу для нахождения эквивалентной емкости последовательно соединенных конденсаторов. 10. Приведите формулу для нахождения эквивалентной емкости параллельно соединенных конденсаторов. |
